 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Структура системы с линейно независимыми сигналами.
Эта система предназначена для многоканальной передачи информации с линейно независимыми канальными сигналами. Условие линейной независимости состоит в том, что равенство При помощи генератора линейнонезависимых функций генерируются линейнонезависимые функции; канальные поднесущие подаются на канальный преобразователь, они перемножаются с квантованными значениями канальных сообщений. Все сигналы суммируются и передаются по линии связи. На приемной стороне выделенное сообщение будет отличаться от переданного вследствие действия помех в линии связи и собственных шумов приемной аппаратуры. При приеме сообщений запускается генератор взаимных функций. Принятое сообщение перемножается с функцией генератора взаимн. ф-й и подается на блок интегрирования, при истечении интегрирования появляется напряжение, пропорциональное квантованным значениям источников. С помощью фильтров получаем необходимый аналоговый сигнал. Квантование по уровню Замена непрерывной шкалы уровней сообщения дискретной шкалой уровней наз. квантованием по уровню. Если мгновенное значение уровней сообщения находится внутри интервала, расположенного между двумя дозволенными дискретными уровнями, то вместо него предается значение, соответствующее ближайшему дозволенному уровню. В результате квантования образуется ступенчатая функция xД(t). Квантование по уровню может осуществляться с равномерным или неравномерным шагом. При равномерном квантовании динамический диапазон изменения сообщения делится на m-1 равных частей (т.е. интервал между всеми уровнями квантования одинаковы). При неравномерном квантовании деление производится на m-1 неравномерных частей. На практике преимущественное применение получило равномерное квантование в связи с простотой технической реализации. Расстояние между соседними дискретными уровнями называется интервалом или шагом квантования ∆х. Оптимальным в смысле точности воспроизведения квантованного сигнала является расположение уровня квантования внутри шагов квантования. Квантование можно рассматривать, как прохождение сообщения через систему, подверженную действию помехи Квантование по уровню практически может осуществляться двумя способами. При первом способе мгновенное значение функции x(t) заменяется меньшим дискретным значением (рис. а).
При втором способе квантования мгновенное значение функций заменяется ближайшим меньшим или большим дискретным значением в зависимости от того, какое из этих значений ближе к мгновенному значению функции. В этом случае переход ступенчатой функции с одной ступени на другую происходит в те моменты, когда первоначальная непрерывная функция x(t) пересекает середину между соответствующими соседними дискретными уровнями (рис. б). Код Хемминга. Предназначенный для обнаружения и исправления однократной ошибки. При построении кода каждый из k проверочных символов определяется как результат суммирования по модулю 2 определенного сочетания информационных символов. В результате этого сумма проверяемых информационных и контрольного символа всегда является четной. Количество контрольных символов определяется по формуле: В коде Хэмминга проверки на четность организованы таким образом, что получается число, указывающее номер позиции, на которой произошло искажение. При проверке на четность мы используем номер позиции соответствующие единице находящейся в том разряде, какую проверку мы делаем, то есть если 1проверка, то смотрим единицы по первому разряду, и т.д. Если число единиц на проверочных позициях четное то контрольный символ равен 0, а если число единиц на проверочных позиция не четное, то контрольный символ равен 1. После окончания проверки мы узнаем, на какой позиции находится ошибочный символ, если таковой имеется, по результату проверок, поскольку оно организовано таким образом, что получается число, указывающее на номер позиции, на которой произошло искажение. Была принята комбинация 1110111.
Сумма парная. В младший разряд номера позиции ошибки записываем 0. Вторая проверка:
позиции ошибки записываем 0. Третья проверка на парность:
Номер позиции, где была ошибка – 100. Этот двоичный код соответствует числу 4. Это значит, что четвёртый символ в принятой комбинации надо заменить на противоположный. Получим комбинацию – 1111111.
Информационные символы находятся на позициях 3, 5, 6, 7 , то есть передавался двоичный код 1111, которому соответствует число 15.
Поиск по сайту: |
 возможно в том, и только в том, случае, когда все коэффициенты
возможно в том, и только в том, случае, когда все коэффициенты  одновременно равны нулю. То есть ни одна из сигнальных функций
одновременно равны нулю. То есть ни одна из сигнальных функций  не может быть представлена линейной композицией других сигнальных функций.
не может быть представлена линейной композицией других сигнальных функций. . Обычно эту помеху наз. шумом квантования. Эта погрешность имеет случайный характер. Возникающая в момент
. Обычно эту помеху наз. шумом квантования. Эта погрешность имеет случайный характер. Возникающая в момент  времени ошибка определяется выражением:
времени ошибка определяется выражением: 

 , где
, где  – количество символов в кодовой комбинации. Контрольные символы располагаются на местах определенных по степеням двойки (1, 2, 4, 8, 16…)
– количество символов в кодовой комбинации. Контрольные символы располагаются на местах определенных по степеням двойки (1, 2, 4, 8, 16…)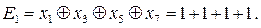 Проведём первую проверку на парность:
Проведём первую проверку на парность: Сумма парная. Во второй разряд номера
Сумма парная. Во второй разряд номера Сумма непарная. В третий разряд номера записываем 1.
Сумма непарная. В третий разряд номера записываем 1.