 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Уравнение нормального распространения пламени.⇐ ПредыдущаяСтр 14 из 14
Задача о тепловом (нормальном) распространении пламени с учётом зависимости скорос -ти реакции от температуры и концентраций реагирующих веществ была решена Я.Б.Зельдови -чем и Д.А.Франк – Каменецким. Опуская математические выкладки, можно записать формулу скорости нормального распространения пламени:
U
где: С Т Т
Ф(T) – объёмная скорость тепловыделения, кВт/м
Проверка показала, что вычисления по формуле (1) скорость распространения пламени в смеси СО с воздухом близка к значениям, полученным из опыта. Однако эта формула не нашла широкого применения для определения U кинетического уравнения и значения констант, который для многих реакций ещё неизвестен.
С целью упрощения задачи Д.А.Франк - Каменецкий заменил истинное распределение температур во фронте пламени ломаной линии, проведя косательную к кривой действитель -ного распределения температур в точке перегиба и продолжив её до пересечения с прямым, параллельными оси абсцисс и отвечающими температурам Т Здесь S Максимальное значение градиента температур во фронте пламени будет:
Поток тепла, поступающий теплопроводностью из зоны химического реагирования:
q = -
расходуется на нагрев поступающей в пламя горючей смеси от температур Т
q = C
где: С Приравнивая выражения (3) и(4) получим уравнение для нормальной скорости распростра - нения пламени: U
т.к. в пламени химической реакции протекают при высоких температурах, в малом интервале температур, то химическая ширина зоны пламени
где k - безразмерный множитель,< 1, который зависит от Т Химическую ширину зоны пламени в свою очередь можно выразить как:
Преобразуя формулу (5) с учётом (6) и(7) получим:
U
Из этой формулы видно, что U Из выражения (5) следует, что
и время прогрева газа в пламени:
т.е. чем больше U
Поиск по сайту: |
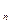 =
=  (1)
(1) – плотность исходной смеси;
– плотность исходной смеси; – теплоёмкость реагирующего газа;
– теплоёмкость реагирующего газа; – температура горения;
– температура горения;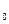 – начальная температура смеси;
– начальная температура смеси; - коэффициент теплопроводности;
- коэффициент теплопроводности;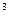 .
.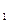 – это расстояние между точками пересечения и представляет собой ширину зоны, в которой происходит изменение температур от Т
– это расстояние между точками пересечения и представляет собой ширину зоны, в которой происходит изменение температур от Т 
 = -
= -  (2)
(2) (3)
(3) (4)
(4)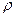 - плотность горючей смеси;
- плотность горючей смеси; (5)
(5) составляет небольшую часть ширины тепловой зоны:
составляет небольшую часть ширины тепловой зоны: (6)
(6) (7)
(7) где:
где:  - время химической реакции во фронте пламени.
- время химической реакции во фронте пламени. (8)
(8) зависит от физических свойств смеси и её реакционной способ ности.
зависит от физических свойств смеси и её реакционной способ ности. (9)
(9)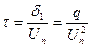 (10)
(10)