 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ. Задача 1.Вы имеете логарифмическую функцию полезности U(W) = lnW и текущий уровень вашего
Задача 1.Вы имеете логарифмическую функцию полезности U(W) = lnW и текущий уровень вашего благосостояния W = 5000 руб. Возможны две ситуации: 1. С вероятностями р = 0,5, q = 0,5 можно выиграть и проиграть 1000 руб. Если вы можете купить страховой полис, который полностью устраняет риск, за 125 руб., купите его или предпочтете игру? 2. Вы играли в лотерею и проиграли 1000 руб. Согласились ли бы вы сыграть во второй раз, купив лотерейный билет за ту же сумму 125 руб.? Решение. 1. Текущее благосостояние игрока Wтек = 5000 руб.
Таким образом, если игра состоится, то в ее итоге материальное состояние игрока будет иметь вид:
Согласно формуле (5.1) ожидаемая полезность игры будет равна: Е(U(W)) = Ожидаемая денежная оценка игры: Е(W) = Оценим уровень благосостояния W*, который соответствует ожидаемой полезности игры E(U(W*)): E(U(W*)) = lnW* = 8,497 ютиля, откуда, потенцируя, получаем: W* = е8,497 = 4899 руб.* (*4899 руб. - сумма, эквивалентная игре в том смысле, что полезность этой суммы и полезность игры равны между собой). Следовательно, премия за риск, т.е. та максимальная сумма, которая может быть уплачена за отказ участвовать в игре, а получить наверняка без риска 4899 руб., равна 5000 - 4899 = 101 руб. Это меньше, чем стоимость страхового полиса, равная 125 руб. Поэтому выгоднее не рисковать и страховой полис не покупать. 2. С учетом сказанного выше в результате факта уже проигранной суммы 1000 руб. текущее материальное благосостояние индивидуума может составлять:
Рассуждая так же, как и выше, и применяя новые указанные цифры материального благосостояния, будем иметь следующее: согласно формуле (5.1) ожидаемая полезность игры будет равна Е(U(W)) = Ожидаемая денежная оценка игры теперь будет Е(W) = Уровень благосостояния W*, который соответствует ожидаемой полезности игры в новых условиях, определяется по формуле E(U(W*)) = lnW* = 8,262 ютиля, откуда W* = е8,262 = 3870 руб. Теперь премия за риск определяется по формуле 4000 - 3870 = 130 руб. Эта сумма больше, чем 125 руб. - неизменная сумма страхового полиса - на 5 руб. Хотя ожидаемый выигрыш и незначительный, но во второй раз имеет смысл купить страховой полис, так как премия за риск (130 руб.) будет больше цены страхового полиса (125 руб.). Следовательно, можно рисковать, покупать страховой полис и участвовать в игре на заданных условиях. Задача 2. Индивид имеет функцию полезности U(W) = Решение. Если игрок принимает игру, то ожидаемая ее полезность согласно формуле (5.1) определяется как Е(U(W)) = Гарантированное благосостояние, которое имеет полезность Е(U(W)) = 3, отвечает формуле E(U(W*)) = 3 = Учитывая 4 руб., имеющиеся у индивида, он готов будет продать свой лотерейный билет за W* = 9 - 4 = 5 руб. или дороже. В результате его гарантированное благосостояние будет иметь заранее определенную полезность, не меньшую чем E(U(W*)) ≥ 3. Задача 3. Пусть функция полезности Неймана-Моргенштерна для бизнесмена А имеет вид U = 10 + 2М, где М - денежный выигрыш (тыс. руб.). Он имеет возможность вложить 25 тыс. руб. в строительство бара и гриля. С вероятностью 0,5 он потеряет весь свой капитал и с той же вероятностью 0,5 выиграет 32 тыс. руб. Требуется определить: 1. Следует ли инвестировать вообще? 2. Если будет сделано инвестирование, то какова будет его ожидаемая полезность? Решение. 1. Если вообще не инвестировать, то выигрыша нет (М = 0) и полезность U(0) = 10 + 2 ∙ 0 = 10. 2. Если инвестировать, то с вероятностью 0,5 (по условию задачи) М = -25, т.е. U(-25) = 10 – 2 ∙ 25 = -40, и с вероятностью 0,5 М = 32 (также по условию задачи). Полезность U(32) оказывается равной U(32) = 10 + 2 ∙ 32 = 74. Следовательно, ожидаемая полезность при инвестировании: Uинв = Таким образом, инвестировать следует, так как Uинв = 17 > U(0) = 10.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Предположим, что функция полезности определяется логарифмической зависимостью U(W) = ln(W), и возникает ситуация, когда можно с равными шансами выиграть и проиграть 1 тыс. руб. Сколько вы готовы заплатить, чтобы избежать риск, если текущий уровень вашего благосостояния равен 10 тыс. руб.? Сколько бы вы заплатили, если бы ваше состояние было 1 млн руб.? Задание 2. Управляющий банком во время своего отпуска желает совершить кругосветное путешествие, которое стоит 10000 долл. Полезность путешествия можно оценить количеством денег, потраченных на отдых (W). Пусть его функция полезности выражается зависимостью U(W) = ln(W). Определите: 1. Если существует вероятность, равная 0,25, потерять во время путешествия 1000 долл., то какова ожидаемая полезность кругосветного путешествия? 2. Отдыхающий банкир может приобрести страховку от потери 1000 долл. за 250 долл., купив, например, дорожные чеки. Покажите, что ожидаемая полезность в случае, когда он покупает страховку, выше по сравнению с ситуацией, когда потеря 1000 долл. происходит без страхования.
Поиск по сайту: |
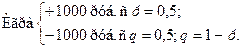

 [(U(6000) + U(4000)] =
[(U(6000) + U(4000)] = 
 . Его начальное состояние равно 4 руб. У него есть лотерейный билет, по которому он с вероятностью 0,5 может выиграть 12 руб. и с вероятностью 0,5 - 0 руб. Какова ожидаемая полезность игры? Какова наименьшая сумма, за которую он продал бы лотерейный билет?
. Его начальное состояние равно 4 руб. У него есть лотерейный билет, по которому он с вероятностью 0,5 может выиграть 12 руб. и с вероятностью 0,5 - 0 руб. Какова ожидаемая полезность игры? Какова наименьшая сумма, за которую он продал бы лотерейный билет?
 , откуда W* = 9.
, откуда W* = 9.