|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЛАМИНАРНЫЙ ПОТОК КАК СТРУКТУРА СКОЛЬЗЯЩИХ ОТНОСИТЕЛЬНО ДРУГ ДРУГА СЛОЁВ (ТЕЛЕСКОПИЧЕСКАЯ МОДЕЛЬ ЭПЮРЫ СКОРОСТЕЙ)
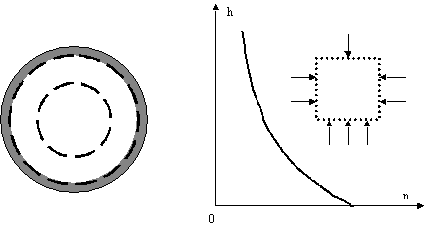
Рассмотрим процесс возникновения гидродинамического потока и процесс перехода от ламинарного движения к турбулентному. Поведение гидродинамического потока определяется числом Рейнольдса
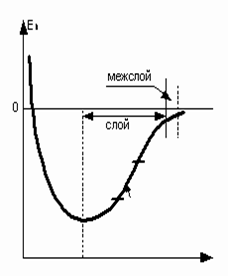
Рис.1
Рис.2 Сегодня принято считать, что жидкость при ламинарном движении перемещается отдельными слоями не перемешивающимися между собой. При этом скорость ламинарного потока в поперечном сечении изменяется от нуля у стенки до максимальной по оси трубы и имеет форму параболы (пунктирная линия на Рис.2). Причем по мере увеличения перепада давления и числа Рейнольдса парабола все более вытягивается. Но жидкость не может двигаться со скоростью меняющейся в поперечном сечении монотонно строго по закону параболы, так как в этом случае все частицы жидкости, двигаясь с различными скоростями, должны будут с течением времени разлететься на большие расстояния друг от друга и разорвать все связи между ними как в парообразном состоянии, когда частицы практически свободны. На это требуется большое количество энергии равное скрытой теплоте парообразования, чего нет в низко температурном и относительно медленном ламинарном потоке. Да и о слоистости в макроскопическом плане при строго параболическом законе скорости говорить не приходится, так как толщина слоя в этом случае будет порядка размеров молекул жидкости. А это уже противоречит наблюдаемым фактам о макроскопических размерах слоёв. Поэтому логично предположить, что ламинарный поток имеет также и слоистую структуру скорости (как на Рис.2). Центральный слой имеет максимальную скорость, затем по мере удаления слоя от центра к стенке скорость слоев снижается и скорость слоя непосредственно контактирующего со стенкой равна нулю. Структура ламинарного потока напоминает телескопическую конструкцию, в которой элементы движутся с различными скоростями, от покоящегося внешнего элемента (пристенный слой), до наиболее быстро движущегося, внутреннего. Выясним причины и механизмы порождающие слоистый характер скорости ламинарного потока и как следствие слоистую структуру самого потока. Выясним также влияние на формирование слоёв различных параметров потока: вязкости жидкости, диаметра трубы, длины трубы, перепада давления на концах трубы, температуры жидкости. Напомним, что для простоты картины мы рассматриваем гидродинамический поток в трубе постоянного круглого сечения. В “динамике эволюции” (см. [Л-2]) предложен механизм бифуркации (видоизменения) состояния диссипативной системы как преодоление кооперативным потоком потенциального барьера встающего на его пути. Таким потенциальным барьером, препятствующим перемещению жидкости в трубе является энергия связи между частицами жидкости и частиц жидкости с частицами стенки трубы. На Рис.1 изображена известная из курса физики диаграмма потенциальной энергии связи (взаимодействия) между частицами в зависимости от расстояния между ними. Для того чтобы жидкость в трубе начала двигаться, необходимо приложить усилие способное разорвать силы сцепления между молекулами жидкости и стенкой, необходимо совершить работу против сил сцепления и преодолеть суммарный потенциальный барьер. Такое усилие порождается неравновесностью системы, перепадом давления на концах трубы. Градиент потенциальной энергии неравновесности и вызывает силу способную преодолеть потенциальный барьер сил сцепления. По мере роста перепада давления на концах трубы возрастают усилия растяжения в жидкости от сечения большего давления к сечению меньшего давления. Наконец наступает момент, когда силы растяжения начинают превосходить силы сцепления и связи последних начинают рваться, формируется межслой. В результате напряжение сил растяжения внутри слоя снимается и частицы слоя начинают двигаться как единое целое с одинаковой скоростью слоя, как целостный элемент, как поршень в цилиндре. Происходит скольжение слоев друг относительно друга. Первый межслой в момент возникновения ламинарного потока формируется между покоящимся пристенным слоем и всей остальной массой жидкости движущейся в этот момент с постоянной скоростью. В силу симметрии задачи межслой имеет форму поверхности цилиндра. На этой поверхности и формируется потенциальный барьер сил сцепления, который необходимо преодолеть силам возникающим как следствие перепада давлений. Зная плотность молекул на цилиндрическом межслое (то есть зная величину потенциального барьера связей в межслое) можно рассчитать величину неравновесности при которой возникает межслой. Возникновение слоев начинается от стенки трубы к центру потока. С одной стороны чем ближе межслой к стенке тем больше его поверхность и соответственно больше потенциальный барьер сил сцепления который необходимо преодолеть. С другой стороны площадь поверхности межслоя зависит от диаметра межслоя линейно, а масса жидкости заключённая в пространстве межслоя – квадратично. Отсюда чем больше диаметр межслоя тем больше масса заключённой в нём жидкости приходящаяся на единицу площади межслоя, или на единицу потенциального барьера. Следовательно чем больше диаметр межслоя тем при меньшей неравновесности (меньшем перепаде давления) можно преодолеть его силы сцепления. Покажем это аналитически. Пусть труба по которой течёт ламинарный поток имеет длину
где: Что бы получить силу связи всего межслоя необходимо (2) умножить на
Запишем силу, которая за счёт перепада давления на концах трубы обепечивает разрыв силы (3) и формирует межслой.
Приравнивая (3) и (4) найдём из полученного равенства перепад давления на концах трубы, необходимый для разрыва сил сцепления и формирования межслоя в зависимости от длины и диаметра межслоя.
Из (5) видно, как и предполагалось, что при постоянной длине трубы, чем больше диаметр межслоя тем меньший перепад давления необходим для его формирования. При движении жидкости всегда наблюдается покоящийся пристенный слой. То есть первый межслой всегда образуется вблизи стенки, но в среде жидкости, хотя самый большой диаметр межслоя находится между стенкой и жидкостью. Это можно объяснить двумя причинами. Во-первых возможно, что силы сцепления между частицами стенки и жидкостью больше чем силы сцепления между частицами жидкости, так называемые смачиваемые поверхности. Во-вторых даже если силы сцепления между частицами жидкости больше чем между стенкой и жидкостью, так называемые не смачиваемые поверхности, то с учётом шероховатости стенки общая площадь взаимодействия между стенкой и жидкостью много больше площади идеального цилиндра межслоя. Поэтому потенциальный барьер первого межслоя реально всегда меньше потенциального барьера связи стенка-жидкость. Заметим, что сила связи между молекулами или вязкость жидкости зависят не только от рода жидкости, но и от температуры жидкости. Привлекаю внимание к понятию температуры с тем чтобы у читателя не сложилось впечатление, что оперируя геометрическими и динамическими понятиями я забываю о статистических закономерностях, всегда мощно присутствующих в многочастичных диссипативных системах. Подробнее о проявлении статистических закономерностей мы поговорим при рассмотрении турбулентного движения. Теперь выясним: почему после разрыва сил сцепления в межслое, масса жидкости находящаяся внутри межслоя не движется с ускорением под действием силы создаваемой перепадом давления, как того требует основной закон динамики? Ведь после разрыва сил связи перепад давления, т.е. сила воздействующая на массу жидкости и создаваемая из вне, не меняется. А опыт показывает, что скорость течения ламинарного потока через трубу постоянного сечения при неизменном перепаде давления на концах трубы не меняется. Объяснить это можно следующим образом. Да, в начальный момент после разрыва сил сцепления между молекулами и образования межслоя, жидкость внутри межслоя начинает двигаться с ускорением. Но далее вступает в действие другой механизм. Силы сцепления между слоями преодолеваются не полностью. В то время как часть связей между частицами преодолевается, одновременно другая часть восстанавливается. Существует динамическое равновесие в межслое между силами сцепления и силами разрыва, вызываемыми внешним перепадом давления. Вообще механизм превращения энергии при возникновении межслоя следующий. После преодоления потенциального барьера сил сцепления в межслое часть потенциальной энергии неравновесности, создаваемой из вне, расходуется на преодоление восстанавливающихся связей, другая часть преобразуется в кооперативную энергию потоков Умова-Пойтинга, в полном соответствии с законом сохранения и превращения энергии. Потенциальная энергия неравновесности, затрачиваемая на разрыв восстанавливающихся связей, в момент разрыва между молекулами сразу преобразуется в хаотическую кинетическую энергию. Другая часть потенциальной энергии неравновесности, преобразовавшаяся в поток кооперативной энергии с Диссипация кооперативной энергии ведет к ослаблению растяжения в межслое и восстановлению связей между слоями. Условие динамического равновесия в межслое, условие ламинарности можно представить в виде:
где n – количество связей в межслое между молекулами принадлежащими разным слоям.
Знак равенства в (6) соответствует моменту перед разрывом связей в межслое при его формировании. Как показано на Рис.-2 скорость ламинарного потока, имея усредненную скорость, изменяющуюся по закону параболы, изменяется ступенчато. В слое скорость постоянна, а в межслое она резко меняется от скорости одного слоя до скорости другого на малой толщине межслоя, порядка размеров частиц жидкости. Так как силы сцепления в межслое разрываются не полностью, то не полностью снимается и растяжение в слое. До момента разрыва связи данная связь служит для передачи кинетической энергии через межслой от быстрого слоя к медленному. Тем самым в ламинарном потоке идёт процесс передачи кооперативной энергии от центра к периферии. Если неравновесность, т.е. перепад давления продолжает нарастать, то вновь нарастает растяжение в массе жидкости до критической величины, при которой начинается формирование нового межслоя и так далее вплоть до начала турбулизации потока, до формирования качественно новой динамической структуры. Рассмотрим образование второго межслоя, который формируется с ростом перепада давления вслед за пристеночным межслоем. Этот момент изображён на Рис.3, где ламинарный поток показан с торца. На рисунке затемнённым кольцом изображена стенка трубы, а пунктирными окружностями обозначены межслои. Межслой большого диаметра – это первый межслой, образующийся в момент возникновения ламинарного потока между покоящимся пристенным слоем и потоком остальной жидкости. Примем его диаметр равным внутреннему диаметру трубы. Положение и диаметр этого межслоя постоянны и не меняются с ростом перепада давления и увеличения скорости потока. Обозначим диаметр этого первого, пристеночного межслоя
Уравнение (7) для пристеночного межслоя, уравнение (8) для второго межслоя, подчёркиваю в момент его образования. В этот момент потенциальный барьер сил сцепления второго межслоя полностью преодолён, но относительная скорость во втором межслое между первым движущимся слоем и вновь образовавшимся вторым ещё равна нулю. В уравнении (7) Доля восстанавливающихся связей в межслое зависит от относительной скорости в межслое между его сторонами:
В уравнении (8) Разделив уравнение (7) на уравнение (8), после простых преобразований получим квадратное уравнение, устанавливающее зависимость диаметра второго межслоя, в момент его образования (когда Второй межслой возникает в связи с тем, что легче преодолеть меньший потенциальный барьер второго межслоя, чем полностью преодолеть больший по величине потенциальный барьер первого межслоя, даже с учётом (9). Для определения третьего межслоя необходимо составить систему 3-х уравнений. Причём для второго межслоя теперь Необходимо отметить тот факт, что по мере увеличения перепада давления, в силу зависимости (9), то есть с уменьшением В момент формирования межслоя в ламинарном потоке происходит бифуркация, т.е. переход к новому состоянию движения. Причём в ламинарном потоке от момента возникновения ламинарного потока до его перехода в турбулентное состояние происходит целый каскад последовательных бифуркаций, сопровождающихся появлением всё новых межслоёв. На бифуркации ламинарного течения не обращали внимание, потому что они при спокойном движении однородной жидкости не заметны не вооружённым глазом.
Рис. 3 Рис. 4
Поиск по сайту: |
 (1). Входящие в него прямо или косвенно величины являются управляющими параметрами потока. Это перепад давления на концах, от которого зависит скорость потока (
(1). Входящие в него прямо или косвенно величины являются управляющими параметрами потока. Это перепад давления на концах, от которого зависит скорость потока (  ), условное проходное сечение (
), условное проходное сечение ( 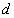 ), вязкость жидкости (
), вязкость жидкости ( 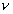 ), определяющая силы сцепления между молекулами жидкости и между молекулами жидкости и стенкой. Для данного конкретного потока прямым управляющим параметром является перепад давления, а остальные параметры являются косвенными, оказывающими влияние только на стадии проектирования (формирующие граничные условия протекания процесса). Рассмотрим поток жидкости через горизонтальную трубу постоянного сечения при переменном, все возрастающем перепаде давления на концах трубы. Трубу принимаем горизонтальной с целью упростить модель и исключить из рассмотрения силы гравитации. В начале при нулевом перепаде давления на концах жидкость в трубе будет находиться в равновесном состоянии. При незначительном перепаде система будет находиться в зоне локального равновесия. Возникающая в результате неравновесности, а значит градиента потенциальной энергии сила мала по величине и не способна преодолеть силы сцепления в жидкости и со стенкой трубы и вызвать кооперативное перемещение массы жидкости. Энергия неравновесности диссипирует в форму хаотического движения в зоне локального равновесия. Отдельные агрегаты молекул в результате самоорганизации будут получать микро кооперативное движение, но под действием нецентрального соударения, являющегося причиной процесса релаксации, оно будет рассеиваться. Подробно о значении нецентрального соударения в процессе релаксации кооперативной энергии в диссипативной среде можно прочесть в [Л-2]. При дальнейшем увеличении неравновесности в системе возрастают силы давления и с некоторого момента они начинают превышать силы сцепления между пристенным слоем, связанным со стенкой и имеющим толщину порядка шероховатостей стенки, и основной массой жидкости. Происходит первая бифуркация в диссипативной среде и формируется диссипативная структура. Возникает поток энергии Умова-Пойтинга, вызывающий поток массовый, ламинарный поток. Между покоящимся пристенным слоем и потоком жидкости возникает межслой в котором происходит скольжение слоев друг относительно друга. Размеры межслоя по толщине того же порядка, что и размеры частиц жидкости. С появлением потока появляется число Рейнольдса. Начинает работать закон сохранения результирующего импульса.
), определяющая силы сцепления между молекулами жидкости и между молекулами жидкости и стенкой. Для данного конкретного потока прямым управляющим параметром является перепад давления, а остальные параметры являются косвенными, оказывающими влияние только на стадии проектирования (формирующие граничные условия протекания процесса). Рассмотрим поток жидкости через горизонтальную трубу постоянного сечения при переменном, все возрастающем перепаде давления на концах трубы. Трубу принимаем горизонтальной с целью упростить модель и исключить из рассмотрения силы гравитации. В начале при нулевом перепаде давления на концах жидкость в трубе будет находиться в равновесном состоянии. При незначительном перепаде система будет находиться в зоне локального равновесия. Возникающая в результате неравновесности, а значит градиента потенциальной энергии сила мала по величине и не способна преодолеть силы сцепления в жидкости и со стенкой трубы и вызвать кооперативное перемещение массы жидкости. Энергия неравновесности диссипирует в форму хаотического движения в зоне локального равновесия. Отдельные агрегаты молекул в результате самоорганизации будут получать микро кооперативное движение, но под действием нецентрального соударения, являющегося причиной процесса релаксации, оно будет рассеиваться. Подробно о значении нецентрального соударения в процессе релаксации кооперативной энергии в диссипативной среде можно прочесть в [Л-2]. При дальнейшем увеличении неравновесности в системе возрастают силы давления и с некоторого момента они начинают превышать силы сцепления между пристенным слоем, связанным со стенкой и имеющим толщину порядка шероховатостей стенки, и основной массой жидкости. Происходит первая бифуркация в диссипативной среде и формируется диссипативная структура. Возникает поток энергии Умова-Пойтинга, вызывающий поток массовый, ламинарный поток. Между покоящимся пристенным слоем и потоком жидкости возникает межслой в котором происходит скольжение слоев друг относительно друга. Размеры межслоя по толщине того же порядка, что и размеры частиц жидкости. С появлением потока появляется число Рейнольдса. Начинает работать закон сохранения результирующего импульса.
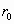

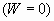
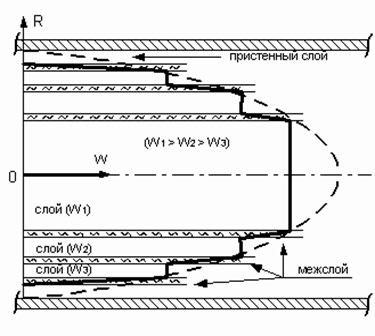
 . Диаметр первого межслоя обозначим через
. Диаметр первого межслоя обозначим через 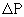 . Найдём зависимость перепада давления, необходимого для формирования межслоя, от диаметра межслоя. Сила связи между молекулами жидкости принадлежащим разным сторонам межслоя, приходящаяся на одно кольцо по окружности межслоя (ширина кольца по длине потока - одна молекула) будет:
. Найдём зависимость перепада давления, необходимого для формирования межслоя, от диаметра межслоя. Сила связи между молекулами жидкости принадлежащим разным сторонам межслоя, приходящаяся на одно кольцо по окружности межслоя (ширина кольца по длине потока - одна молекула) будет:
 (2)
(2) - количество молекул в среде жидкости, приходящееся на единицу длины, в (2) это будет число пар молекул разных слоёв на единицу длины окружности межслоя, которые необходимо разорвать;
- количество молекул в среде жидкости, приходящееся на единицу длины, в (2) это будет число пар молекул разных слоёв на единицу длины окружности межслоя, которые необходимо разорвать; 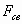 - сила связи между молекулами жидкости, зависящая от вязкости жидкости (см. Рис.1).
- сила связи между молекулами жидкости, зависящая от вязкости жидкости (см. Рис.1).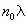 .
. (3)
(3) (4)
(4) (5)
(5)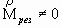 , начинает диссипировать в хаотическую форму вследствие действия эффекта вырождения результирующего импульса в многочастичной среде. Устанавливается равновесие между мощностью процесса производства кооперативной энергии и мощностью процесса диссипации кооперативной энергии. В результате этого равновесия мы и наблюдаем равномерное движение ламинарного потока в трубе постоянного геометрического сечения. Вся диссипация кооперативной энергии в ламинарном потоке происходит только в зоне межслоя, т.к. сам слой движется как единое целое. Восстановление связей в межслое происходит по причине того, что частицы жидкости по своему энергетическому состоянию находятся внутри потенциальной ямы, изображённой на Рис.1. Мы не говорим, что восстанавливаются связи тех же частиц, мы говорим о количественном соотношении.
, начинает диссипировать в хаотическую форму вследствие действия эффекта вырождения результирующего импульса в многочастичной среде. Устанавливается равновесие между мощностью процесса производства кооперативной энергии и мощностью процесса диссипации кооперативной энергии. В результате этого равновесия мы и наблюдаем равномерное движение ламинарного потока в трубе постоянного геометрического сечения. Вся диссипация кооперативной энергии в ламинарном потоке происходит только в зоне межслоя, т.к. сам слой движется как единое целое. Восстановление связей в межслое происходит по причине того, что частицы жидкости по своему энергетическому состоянию находятся внутри потенциальной ямы, изображённой на Рис.1. Мы не говорим, что восстанавливаются связи тех же частиц, мы говорим о количественном соотношении.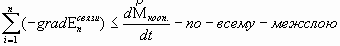 ( 6 )
( 6 ) - разность кооперативных импульсов n молекул соседних слоев.
- разность кооперативных импульсов n молекул соседних слоев. , а диаметр второго межслоя
, а диаметр второго межслоя 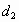 . Составим уравнение равновесия в межслоях между силами разрыва, вызываемыми перепадом давления на концах трубы и силами сцепления между сторонами межслоя (согласно (3)) в момент образования второго межслоя.
. Составим уравнение равновесия в межслоях между силами разрыва, вызываемыми перепадом давления на концах трубы и силами сцепления между сторонами межслоя (согласно (3)) в момент образования второго межслоя.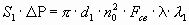 (7)
(7) (8)
(8)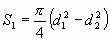 - площадь кольца на которую действует сила перепада давления
- площадь кольца на которую действует сила перепада давления 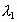 - доля восстанавливающихся связей в первом межслое.
- доля восстанавливающихся связей в первом межслое. (9);
(9); 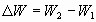 - относительная скорость в межслое, разность скоростей жидкости по сторонам межслоя. Относительная скорость для пристеночного межслоя равна скорости первого движущегося слоя.
- относительная скорость в межслое, разность скоростей жидкости по сторонам межслоя. Относительная скорость для пристеночного межслоя равна скорости первого движущегося слоя.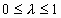 ;
; 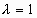 - соответствует моменту перед началом образования межслоя.
- соответствует моменту перед началом образования межслоя. 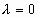 - соответствует полному разрыву связей в межслое. Зависимость (9) очень важна для расчёта структуры ламинарного потока. Для получения этой зависимости в явном виде в зависимости от рода жидкости, температуры, величины относительной скорости нужны глубокие знания квантовой физики, которых нет у автора статьи. За то, что такая зависимость существует говорит во-первых график рисунка 1, во-вторых без полного разрыва связей в межслое (
- соответствует полному разрыву связей в межслое. Зависимость (9) очень важна для расчёта структуры ламинарного потока. Для получения этой зависимости в явном виде в зависимости от рода жидкости, температуры, величины относительной скорости нужны глубокие знания квантовой физики, которых нет у автора статьи. За то, что такая зависимость существует говорит во-первых график рисунка 1, во-вторых без полного разрыва связей в межслое ( 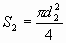 - площадь внутреннего слоя, на которую действует сила преодолевающая потенциальный барьер сил сцепления второго межслоя. В уравнении (8)
- площадь внутреннего слоя, на которую действует сила преодолевающая потенциальный барьер сил сцепления второго межслоя. В уравнении (8) 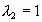 , так как мы рассматриваем момент образования межслоя, когда относительная скорость ещё равна нулю.
, так как мы рассматриваем момент образования межслоя, когда относительная скорость ещё равна нулю. (10). В (10)
(10). В (10) 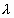 будет меньше единицы и зависит от относительной скорости во втором межслое. И так далее вплоть до начала турбулизации потока
будет меньше единицы и зависит от относительной скорости во втором межслое. И так далее вплоть до начала турбулизации потока