 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Переход ламинарного течения в турбулентноеСтр 1 из 19Следующая ⇒
Перевод Переход ламинарного течения в турбулентное смена режима движения вязкой жидкости, наблюдаемая в некоторой области пограничного слоя или каналах, следах и т. п., происходящая из-за потери устойчивости ламинарного потока. Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия. Главный редактор Г.П. Свищев. 1994. Турбулентность [править] Материал из Википедии — свободной энциклопедии О фильме с таким названием см. Турбулентность (фильм).
Вихревая дорожка при обтекании цилиндра
Ламинарное (на переднем плане) и турбулентное течение вокругсубмарины «Лос-Анджелес»
Турбуле́нтность, устар. турбуле́нция (от лат. turbulentus — бурный, беспорядочный), турбуле́нтное тече́ние — явление, заключающееся в том, что при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности. Волны появляются случайно. То есть их размер и амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально ее можно наблюдать на конце струи пара из электрочайника. Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах.
Обычно турбулентность наступает при превышении некоторого критического параметра, например числа Рейнольдса или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды). При определённых параметрах турбулентность наблюдается в потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовыхБозе- и Ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении. Турбулентность возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности. Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно. Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются вокруг средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией. Турбулентность, например, можно создать: § увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды); § увеличив число Релея (нагреть среду); § увеличив число Прандтля (уменьшить вязкость); § задав очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств. § создав сложные граничные или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Можно, например, организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств. § создав квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии. § облучив среду звуком высокой интенсивности. § с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.
[править]Теория
При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создаётся одинаковая картина разгара, несмотря на разную начальную скорость. Фрактальный — означает самоподобный. У прямой линии фрактальная размерность равна единице. У плоскости равна двум. У шара трём. Русло реки имеет фрактальную размерность больше 1, но меньше двух, если рассматривать его с высоты спутника. У растений фрактальная размерность вырастает с нуля до величины больше двух. Есть характеристика геометрических фигур, называется фрактальная размерность. Наш мир нельзя представить в виде множества линий, треугольников, квадратов, сфер и других простейших фигур. И фрактальная размерность позволяет быстро характеризовать геометрические тела сложной формы. Например, у осколка снаряда. Нелинейная волна — волна, которая обладает нелинейными свойствами. Их амплитуды нельзя складывать при столкновении. Их свойства сильно меняются при малых изменениях параметров. Нелинейные волны называют диссипативными структурами. В них нет линейных процессов дифракции, интерференции, поляризации. Но есть нелинейные процессы, например, самофокусировка. При этом резко, на порядки увеличивается коэффициент диффузии среды, перенос энергии и импульса, сила трения на поверхность. То есть, в частном случае, в трубе с абсолютно гладкими стенками при скорости выше некоторой критической, в течение любой сплошной среды, температура которой постоянная, под действием только силы тяжести всегда самопроизвольно образуются нелинейные самоподобные волны и затем турбулентность. При этом нет никаких внешних возмущающих сил. Если дополнительно создать возмущающую случайную силу или ямки на внутренней поверхности трубы, то турбулентность также появится. В частном случае нелинейные волны — вихри, торнадо, солитоны и другие нелинейные явления (например, волны в плазме — обычные и шаровые молнии), происходящие одновременно с линейными процессами (например акустическими волнами). На математическом языке турбулентность означает, что точное аналитическое решение дифференциальных уравнений в частных производных сохранений импульса и сохранения массы Навье-Стокса (это закон Ньютона с добавлением сил вязкости и сил давления в среде и уравнение неразрывности или сохранения массы) и уравнение энергии представляет собой при превышении некоторого критического числа Рейнольдса, странный аттрактор. Они представляют нелинейные волны и обладают фрактальными, самоподобными свойствами. Но так как волны занимают конечный объём, какая-то часть области течения ламинарна. При очень малом числе Рейнольса — это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров. Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью. Например, изменяя диаметр трубы, мы управляем числом Рейнольдса, расходом топлива и скоростью заполнения бака ракеты. Уравнения Навье — Стокса (обычные, а не усреднённые по какому-то интервалу времени) описывают и мягкую, и жёсткую потерю устойчивости течений. Их можно вывести тремя способами из общих законов сохранения: постулируя закон трения Ньютона(обобщённый), следуя методу Чепмена-Энскога и из метода Грэда. При вязкости равной нулю уравнения сводятся к уравнению Эйлера. Точные решения уравнения Эйлера также хаотичны. Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюсмгновенной составляющей: U = Ucp + u' = 100 м/c + 0.5 м/с. Здесь u' — пульсационная составляющая или пульсация. Удобно оказалось ввести степень турбулентности: e = 100 %*u'/Ucp = 100 %*0.5/100 = 0,5 %. Для трёх осей: e = (u' + v' + w')/Ucp. Турбуленое течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое. Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени. Теория однородной турбулентности (то есть, при очень больших числах Рейнольдса, когда её статистические параметры не зависят от времени и примерно постоянны в течении, но зависят от направления) была создана советскими учёными Обуховым и Колмогоровым. И использовалась затем во многих инженерных расчётах. Теория привела к созданию упрощённых полуэмпирических моделей течения: k-ε (ка-эпсилон) и многих других. Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т. п.), в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твёрдых тел, в следах за такими телами и т. п.) турбулентны из-за наличия источников энергии и импульса, наличия внешних возмущающих сил или отсутствия сил сопротивления трения в квантовых жидкостях. При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе То есть, турбулентность может возникать самопроизвольно, а может в результате действий нескольких внешних сил. При изучении течения жидкости через трубки малого диаметра французским врачом и учёным Пуазейлем в 1840—1842 гг. выведена формула, по которой можно рассчитать расход воды через трубу.[1][2] До Пуазейля исследованием движения вязкой жидкости через трубы малого диаметра занимался Хаген (1797—1884). При большом расходе формула оказалась неверной. Причина в том, что в трубе возникала турбулентность. Стоксом, английским учёным-теоретиком были найдены решения уравнения движения вязкой жидкости для малых чисел Re (это второй закон Ньютона с добавками сил давления и сил вязкости), которые он вывел в 1845 г. для движения жидкости в круглой трубе. Затем он получил формулу силы сопротивления при равномерном движении шара в неограниченной жидкости в 1851 году. Её стали использовать для определения коэффициента динамической вязкости. Но решения совпали с опытом лишь при малых скоростях движения жидкости и диаметрах трубы и шара. Причина этого расхождения была объяснена только опытами Рейнольдса в 1883 г. Он показал существование двух различных режимов движения жидкости — ламинарного и турбулентного — и нашёл один параметр — число Рейнольдса — который позволил предсказать, наличие турбулентности для данного течения в трубе. Если бы Стокс нашёл точные решения Навье-Стокса, он бы обнаружил турбулентность теоретически. Это позволило Рейнольдсу в 1883 г. ввести положение, что течения одинакового типа (труба должна быть геометрически подобной) с одинаковым числом Рейнольдса подобны. Этот закон был назван законом подобия. Затем, на основе опытов, стала развиваться теория размерности и подобия. Так как Хаген не знал, как выглядят уравнения Навье-Стокса, что такое число подобия Рейнольдса, то нельзя говорить, что он или Леонардо да Винчи открыл турбулентность. Они наблюдали хаотическое движение в воде. Но описать количественно, предсказать его наступление не могли. А подобие течения, рождение самоподобных структур, например вихрей, которые сами состоят из таких же вихрей — основное свойство турбулентности. То есть Рейнольдс как бы открыл то, что уравнение для силы гравитации и закон Кулона подобны с разницей только в коэффициенте. А Хаген и Пуазейль только нашли отдельные параметры, которые входят в точное решение уравнения Навье-Стокса и влияют на течение. Частичное описание развитой турбулентности в рамках математики XIX века предложил Л. Ричардсон в начале XX века. Мешая ложкой чай в стакане, мы создаём вихри размером порядка размера стакана, ложки. Вязкость действует на течение тем сильнее, чем меньше характерный размер течения. Под характерным размером понимают какой-то геометрический параметр, сильно влияющий на течение. Диаметр стакана, его высота, ширина ложки. При большом числе Рейнольдса на эти крупномасштабные движения молекулярная вязкость действует слабо. Уравнение движения жидкости (Навье-Стокса) нелинейно, так как скорость жидкости переносится самой скоростью и эти вихри неустойчивы. Они дробятся на более мелкие вихри, те на более мелкие. В конце концов на малых размерах вступает в действие молекулярная вязкость, и самые мелкие вихри затухают за счёт неё. Эта представление назвали прямой каскад (или переход от больших масштабов в меньшие). Турбулентность формально связана с биологическими объектами, с процессами митоза и роста некоторых раковых опухолей, с теорией радиоактивного распада, с процессами, происходящими на рынках акций. Есть разница между понятием турбулентность и турбулентное течение. Термин турбулентное течение возник в гидравлике. Затем были открыты квантовые жидкости. Их вязкость всегда равна нулю. Если подсчитать для них число Рейнольдса, оно всегда равно бесконечности, когда проекция вектора скорости не равна нулю. Само турбулентное течение может присутствовать в системе очень мелких вихрей, в некоторых малых частях среды. Поэтому, средняя скорость течения равна нулю, когда квантовая жидкость покоится в сосуде. Число Рейнольдса не определено (в числителе нулевая скорость, в знаменателе нулевая вязкость). [править]В советской науке До 1917 года в российской науке пользовались термином беспорядочное течение. В 1938 году Капицей было открыто турбулентное течение в квантовых средах — сверхтекучем гелии. В жидком гелии есть два типа звука — первый и второй, они могут создавать волновую турбулентность на его поверхности. В 1941 году А. Н. Колмогоровым и A. М. Обуховым создана теория однородной турбулентности для несжимаемых течений при больших числах Re. Затем в 1960-е годы было начато изучение нелинейных волн, солитонов. В 1970-е годы в СССР Захаровым Владимиром Евгеньевичем была изучена слабая или «волновая» турбулентность волн на поверхности воды (её называют вырожденной). Турбулентность внутри сред назвали сильной. В 1975 году введено понятие фрактал математиком Бенуа Мандельбротом. А константа Фейгенбаума, используемая при описании фрактальной среды с детерминированным хаосом, была получена в 1978. Тогда же был открыт сценарий Фейгенбаума (или субгармонический каскад) — частный вид перехода к турбулентности. Физикам было непонятно, почему при хаотическом движении, похожем на Броуновское, в жидкости или газе вдруг миллиарды молекул сворачиваются в кольцо. В начале 80-х годовЮ. Л. Климонтович, профессор МГУ им. Ломоносова, выдвинул гипотезу[источник не указан 306 дней] о том, что турбулентность — это не хаотичное, а высокоорганизованное, упорядоченное течение. И что энтропия при переходе от ламинарного к турбулентному течению уменьшается. Поэтому спонтанно образуются различные структуры. Он предложил свой критерий, на основе «S-теоремы», по которому можно было рассчитать степень упорядоченности сплошной среды, используя величину производства энтропии. Он не знал, что сценарий Фейгенбаума и другие их виды встречаются в реальных турбулентных средах и считал, что модели сплошной среды недостаточно для появления турбулентности и в уравнении Навье-Стокса нет турбулентности. Поэтому даже для простого движения воды он вводил в уравнения некие искусственные дополнительные флуктуационные члены, что было ошибкой[источник не указан 306 дней]. Аналогично вводил дополнительные члены в уравнения сохранения импульса или движения О. Рейнольдс. Его «S-теорема» была очень плохо изложена для экспериментаторов и было непонятно, как её применять в эксперименте и чем она лучше понятия K-энтропии[источник не указан 306 дней]. Она противоречила многолетней практике инженеров. Они часто использовали подход, когда энтропия была постоянной для течения (модель изэнтропического газа). [править]Турбулентность в природе Животные умеют пользоваться турбулентностью. Обычно они подавляют её и управляют её структурой, умеют извлекать энергию из набегающего потока (или ждут попутного ветра). Например, у некоторых из них очень гладкая кожа. Форма поверхности тела такова, что её кривизна — гладкая функция. То есть ваше изображение в зеркале, изготовленном в виде тела дельфина, будет плавно, без изломов меняться на большей части поверхности. Площадь, где кривизна претерпевает разрывы, минимальна. Они используют слизь на коже или перья, шерсть для разрушения поверхностных волн, которые потребляют много энергии, когда образуются при взмахе крыла или движении хвоста. Кончик крыла или плавника всегда острый, чтобы размер волны, образованной на конце, был минимальный. У китов есть канавки, проходящие вдоль тела от рта, создающие особую структуру турбулентного течения. Мухи (за счёт волосков на теле), бабочки (под микроскопом видны системы на крыльях, как решётки чешуек) и птицы используют машущий полет. Они создают вихри в полете, которые позволяют им развить в разы большую подъёмную силу, чем планер того же веса, и достичь большей скорости, тратя меньше энергии. [править]Турбулентность в технике Её стараются либо подавить, либо искусственно создать. Например, при строительстве Норильского комбината было обнаружено, что малый диаметр труб, в котором течение турбулентно, не приводит к увеличению расхода подаваемого воздуха в доменную печь при увеличении внешнего давления подаваемого воздуха. Поэтому были вынуждены поставить параллельно ещё одну трубу, подающую воздух. Причиной этого явления является звуковое запирание трубы, когда скорость потока в трубе достигает скорости звука и дальше расти не может. У самолётов ставят винглеты — загнутые кверху законцовки крыла. Они экономят до 4 процентов топлива, так как при этом уменьшается размер и число образуемых за крылом вихрей, которые уносят с собой полезную кинетическую энергию (это так называемые волновые потери). В тех случаях, когда возникает переходный режим от ламинарного к турбулентному, могут возникать колебания давления, подъёмной силы. Поэтому по всей длине крыла ставят вихрегенераторы (изогнутые скобы). Они стабилизируют параметры потока. Течение после них всегда турбулентно. Поэтому подъёмная сила крыла постепенно растёт с увеличением скорости самолёта. Когда нужно быстро перемешать топливо с воздухом и сжечь его, ставят специальные устройства: центробежные и струйные форсунки в камере сгорания. Они, как и выбранная длина камеры сгорания, обеспечивают полное сгорание топлива. [править]Виды турбулентности § Двумерная турбулентность. Получается в искусственно создаваемой мыльной плёнке воды толщиной от 4 до 5 микрон[3]. § Оптическая турбулентность. Очень мощный луч лазера проходит через стекло и начинает рассеиваться хаотически, сам на себе. Свет — это волны, поэтому это турбулентность световых волн. Хаотичное мерцание звёзд на ночном небе связано с случайным изменением плотности воздуха. Это так же проявление турбулентности. § Речная турбулентность. Течение воды в реке турбулентно. Но за сотни тысяч лет русло реки не может не менять свою форму. Когда число Рейнольдса и расход меняется, река меняет шероховатость своего дна. Река — одна из самых совершенных самоуправляющихся систем в неорганическом мире. § В жидких кристаллах (нематиках), когда скорость среды равна нулю, наблюдается так называемая «медленная» турбулентность. § Химическая турбулентность. В частном случае, она может быть описана уравнением В. Н. Николаевского.[4]. § Кварк-глюонная плазма, которая существовала на ранней стадии Вселенной, описывается моделью идеальной жидкости (то есть уравнением Навье-Стокса с величиной вязкости, равной нулю). Это пример турбулентного состояния плазмы. § Однородная и изотропная § Изотропная — когда её статистические параметры не зависят от направления. Создаётся искусственно на некотором расстоянии после металлической сетки или решётки. § Однородная — когда её параметры меняются вдоль выбранной оси, но в данном сечении (например, трубы́) они одинаковы. § На поверхности вибрирующейся многофазной жидкости. Например, в слое стеклянных сфер в кукурузном крахмальном сиропе при частоте 120 Гц и виброускорении в 25 g.
[править]Литература § Reynods O., An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. Roy. Soc., London, 1883, v.174 § Feigenbaum M., Journal Stat Physics, 1978, v.19, p. 25 § Feigenbaum M., Journal Stat Physics, 1979, v.21, p. 669 § Фейгенбаум M., Успехи Физических наук, 1983, т.141, с. 343 [перевод Los Alamos Science,1980,v.1, p. 4] [1] § Ландау Л.Д, Лифшиц Е. М. Гидродинамика, — М.: Наука, 1986. — 736 с. § Монин А. С., Яглом А. М., Статистическая гидромеханика. В 2-х ч. — Санкт-Петербург: Гидрометеоиздат , Ч. 1, 1992. — 695 с;, Москва, Наука Ч. 2, 1967. — 720 с. § Обухов А. М. Турбулентность и динамика атмосферы «Гидрометеоиздат» 414 стр. 1988 ISBN 5-286-00059-2 § Проблемы турбулентности. Сборник переводных статей под ред. М. А. Великанова и Н. Т. Швейковского. М.-Л., ОНТИ, 1936. — 332 с. § Д. И. Гринвальд, В. И. Никора, «Речная турбулентность», Л.,Гидрометеоиздат, 1988,152 с. § П. Г. Фрик. Турбулентность: модели и подходы. Курс лекций. Часть I. ПГТУ, Пермь, 1998. — 108 с. Часть II. — 136 с. § П. Берже, И. Помо, К. Видаль, Порядок в хаосе, О детерминистическом подходе к турбулентности, М, Мир, 1991, 368 с. § K.E. Gustafson, Introduction to partial differential equations and Hilbert space methods — 3rd ed.,1999 § Introducing Fractal Geometry, Nigel Lesmoir Gordon, Will Rood, Ralph Edney, Icon Books,Totem Books, 2000, 176 p. § Д. Глейк, Хаос, Создание новой науки, 1988,Penguin books, 354 с (написана журналистом для школьников и студентов) http://www.infanata.org/science/1146125509-xaos-sozdanie-novoj-nauki.html § Ю. Л. Климонтович, Статистическая теория открытых систем, Москва, ТОО Янус, 1995. −624 с. § Recent Advances in Engineering Science (Springer — Verlag, Berlin. 1989), V. N. Nikolaevskii. § http://www.lehigh.edu/~jdg4/publications/Ext_Chaos.pdf § Dan Tanaka, Chemical turbulence equivalent to Nikolavskii turbulence, PHYSICAL REVIEW E 70, 015202(R), 2004 § Г. Голдстейн, Классическая механика,Кембридж, 1950, 408 с. § Л. Ц. Аджемян, М. Ю. Налимов,Принцип максимальной хаотичности в статистической теории развитой турбулентности. II. Изотропная затухающая турбулентность,1992 § http://www.mathnet.ru/php/getFT.phtml?jrnid=tmf&paperid=5578&what=fullt&option_lang=rus § http://www.mathnet.ru/php/getFT.phtml?jrnid=tmf&paperid=1497&what=fullt&option_lang=rus [править]См. также ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ. ИЗОТЕРМИЧЕСКИЕ ТЕЧЕНИЯ (ГЕРШУНИ Г.З. , 1997), ФИЗИКА Рассматриваются основные положения современной теории гидродинамической неустойчивости. Принят исторический подход - с момента зарождения теории до современных численных и экспериментальных ее подтверждений. Обсуждаются основные механизмы неустойчивости изотермических течений. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ. ИЗОТЕРМИЧЕСКИЕ ТЕЧЕНИЯ Г. З. ГЕРШУНИ Пермский государственный университет ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ Начнем с вопроса, который на элементарном уровне, по-видимому, всем понятен. Известно, что медленное течение жидкости (в этом можно убедиться наблюдая течение воды из водопроводного крана) является плавным, упорядоченным, регулярным. Такое течение принято называть ламинарным. Но если увеличивать скорость течения, происходит внезапный переход к другой форме течения - турбулентной, когда жидкость течет крайне нерегулярно, неупорядоченно, запутанно, хаотически. Элементы жидкости при этом совершают беспорядочные броски, и только в среднем можно говорить о течении в ту или иную сторону. Этот факт (наличие двух форм движения) известен с давних пор, но только в 80-х годах прошлого столетия Осборн Рейнольдс предпринял систематическое изучение перехода от ламинарной формы течения к турбулентной. Он наблюдал ламинарно-турбулентный переход при течении жидкости в круглых каналах разных диаметров, причем варьировался напор жидкости (и, стало быть, средняя скорость течения) и рассматривались разные жидкости с разной вязкостью. Он установил замечательную закономерность, касающуюся критической скорости перехода. Оказалось, что она (критическая скорость) пропорциональна вязкости жидкости и обратно пропорциональна диаметру трубки. Это можно записать в виде Здесь uk - критическая средняя скорость, n - коэффициент вязкости, d - диаметр трубки, а C - константа, которая может зависеть от формы поперечного сечения. Формулу (1) можно переписать так: Стоящее в левой части отношение является безразмерным числом, названным числом Рейнольдса в честь исследователя. Таким образом, течение жидкости по каналу можно характеризовать числом Рейнольдса Если число Рейнольдса мало, течение ламинарное, если велико - турбулентное, и существует критическое значение числа Рейнольдса при котором происходит ламинарно-турбулентный переход, смена ламинарной и турбулентной фаз движения. Как позже выяснилось, переход от ламинарной формы к турбулентной происходит не только при течении в трубе (канале). Можно сказать, что он характерен почти для всех течений вязкой жидкости. В частности, обтекание жидкостью крыла, профиля корабля или подводной лодки, тела рыбы или птицы также характеризуется ламинарно-турбулентным переходом, причем формула (2) сохраняет вид, только теперь вместо d нужно в нее подставить характерный размер обтекаемого тела L, а константа C будет зависеть от формы тела. Важным свойством турбулентного течения (по сравнению с ламинарным) является высокое сопротивление. При прокачивании жидкости по каналу в режиме турбулентного движения приходится преодолевать гораздо большее сопротивление, чем при ламинарном движении. Это более или менее ясно. Ведь сопротивление происходит из-за того, что текущая по каналу жидкость отдает момент количества движения стенкам. В ламинарном режиме это происходит из-за вязкости, точнее, из-за трения жидкости о стенку. В турбулентном же режиме в этой передаче участвуют весьма энергичные турбулентные завихрения, пульсации, это как бы увеличивает эффективную вязкость. Именно с этим связано увеличение сопротивления при течении вязкой жидкости в турбулентном режиме. ТУРБУЛЕНТНОСТЬ - ЭТО ХОРОШО ИЛИ ПЛОХО? Как и всякий вопрос, заданный в лоб, он не имеет однозначного ответа. Хотелось бы сказать, что турбулентность - это, конечно, плохо. Ведь, как уже говорилось, турбулентный режим означает высокое сопротивление. Как бы удалось сэкономить на мощности насосов, прокачивающих жидкость по каналу, если бы режим течения был ламинарным, то есть если бы удалось погасить турбулентность или затянуть ламинарно-турбулентный переход! Аналогичным образом была бы достигнута огромная экономия по мощности двигателей кораблей и подводных лодок, если бы режим обтекания был ламинарным. Однако взглянем на дело с другой стороны. Пусть мы имеем технологический аппарат, и задача заключается в том, чтобы растворить в жидкости некий объем газа и размешать его равномерно по объему жидкости. Обычно это делается в режиме течения жидкостей - при этом достигается непрерывность производства. Ясно, что в случае ламинарного течения это сделать очень трудно, поскольку в этом режиме практически отсутствует перемешивание отдельных слоев жидкости. Другое дело - турбулентный режим, отличающийся весьма интенсивным перемешиванием. В этом случае газ будет равномерно распределен по объему жидкости без особого труда. Итак, невозможно однозначно оценить турбулентность и сказать, хорошо это или плохо. Ответ определяется обстоятельствами. Однако, разбирая эти простые примеры, мы вышли на существенный вопрос, важность которого очевидна. Очевидно, что необходимо научиться управлять ламинарно-турбулентным переходом: затягивать его или, наоборот, провоцировать его развитие "раньше", то есть при меньших числах Рейнольдса. Понятно, что, прежде чем браться за решение этого важного с практической точки зрения вопроса, необходимо предварительно ответить на главный вопрос, который будет обсуждаться в следующем разделе. ОТЧЕГО ПРОИСХОДИТ ЛАМИНАРНО-ТУРБУЛЕНТНЫЙ ПЕРЕХОД Именно этот вопрос для нас сейчас является главным. Ответ на него был сформулирован Рейнольдсом и практически одновременно лордом Рэлеем, замечательным исследователем, обогатившим гидродинамику множеством важнейших результатов. Ответ может быть дан в таком виде: переход к турбулентности наступает вследствие неустойчивости течения жидкости. Здесь требуется пояснение. Первоначальное понятие устойчивости-неустойчивости дается в школьном курсе на примере материальной частицы. Представим себе материальную частицу, находящуюся в одном из двух потенциальных полей: на дне потенциальной ямы и на вершине потенциального холма (рис. 1). И в том и в другом случае мы имеем равновесие, но эти равновесия отличаются одно от другого драматически. В случае а возникшее по какой-либо (может быть, случайной) причине возмущение вызывает в системе реакцию, направленную на то, чтобы это возмущение погасить. В случае б возникающее возмущение вызывает в системе обратную реакцию: возмущение будет со временем нарастать и система никогда не вернется в исходное состояние. Теперь вернемся к текущей жидкости. Если сформулированная концепция правильна, то, значит, при малых скоростях (малые числа Рейнольдса) возникающие возмущения не имеют видов на длительное существование, они гаснут со временем и система приходит в свое первоначальное состояние. При больших числах Рейнольдса, наоборот, поток не может бороться с возмущениями, возникающими в нем. Появившись, они будут нарастать со временем. Зарождаясь в различных точках потока, нарастая со временем и накладываясь на основное течение, эти возмущения и создают ту запутанность и беспорядочность потока, которую мы отождествляем с турбулентностью. Такова основная идея. Она выглядит достаточно убедительно, но это еще не основание, чтобы признать ее правильной. Для этого нужно солидное экспериментальное подтверждение. ПРОСТЕЙШИЙ СЛУЧАЙ ОПЫТНОЙ ПРОВЕРКИ ИДЕИ Итак, переход к турбулентности связан с неустойчивостью, а неустойчивость, в свою очередь, - с возникновением и развитием возмущений. Откуда же в реальной физической системе, какой является движущая жидкость, могут зародиться возмущения? Источников возмущений очень много. Прежде всего реальная установка (канал с движущейся жидкостью) находится на лабораторном столе, которому передаются колебания от стен и пола здания - результат сотрясения из-за проехавшей по соседству машины или, может быть, даже слабого сейсмического возмущения. Далее, вход жидкости в канал практически никогда не бывает идеально гладким, на входе в жидкость вносятся входные возмущения, они движутся вдоль жидкости вместе с ней и могут при благоприятных (неблагоприятных?) условиях нарастать. Стенки канала почти никогда не бывают лишены неровностей, шероховатостей. Обтекающий эти шероховатости поток непрерывно возмущается. Этот список можно было бы продолжать долго. Но есть источник возмущений, принципиально неустранимый. Это так называемые флуктуации. Когда мы говорим, например, что в данной точке потока плотность постоянна, это лишь означает, что она постоянна в среднем. Около этого среднего значения происходят малые, но макроскопические отклонения в ту или другую сторону. Они приводят к макроскопическим (малым) отклонениям (флуктуациям) давления, температуры и скорости. Флуктуации, таким образом, являются постоянно действующим источником возмущений, в принципе неустранимым. Поставим теперь (мысленно) эксперимент по ламинарно-турбулентному переходу в трубе конечной длины. Вход в трубу постараемся сделать, насколько это возможно, гладким и постепенным, пытаясь устранить возмущения на входе. От шероховатости стенок также попытаемся отделаться благодаря тонкой шлифовке поверхности. Тот факт, что труба имеет конечную длину, также играет важную роль: представим себе, что в потоке жидкости возникло малое возмущение, которое, во-первых, сносится потоком вниз по течению и, во-вторых, в условиях неустойчивости нарастает. Для его роста требуется некоторое характерное время. Требуется время и для сноса возмущения потоком, оно просто равно (по порядку величины) длине трубы, поделенной на скорость потока. Если характерное время нарастания возмущения больше времени сноса, то оно не успеет вырасти на рабочем участке трубы и будет вынесено за его пределы. Если поставить опыт с учетом сделанных оговорок, то получится, что такие важные источники возмущений, как вход и шероховатость стенок, почти полностью устраняются, а те возмущения, которые все-таки возникнут, будут вытеснены потоком за пределы рабочего участка. Результаты такого опыта оказываются удивительными: удается существенно отодвинуть порог возбуждения турбулентности, критическое число Рейнольдса, таким образом, удается увеличить на 2-3 порядка, происходит "затягивание порога турбулентности". Можно поставить также опыт с регулируемой шероховатостью стенок. Уменьшить шероховатость можно лишь до определенного предела, скажем до молекулярных размеров. Но можно ее искусственно увеличить, наклеивая на стенки, допустим, мелкие кристаллики контролируемых размеров. Таким образом, удается создать целую гамму трубок с оцениваемой наперед шероховатостью. Опыт говорит, что в этих случаях порог ламинарно-турбулентного перехода также изменяется в довольно широких пределах, причем критическое число Рейнольдса возрастает с уменьшением шероховатости. Эти простые опыты говорят о том, что идея связать переход к турбулентности с гидродинамической неустойчивостью здравая. Но для полного спокойствия необходимо, скажем, на примере какой-либо задачи детально сравнить получаемое теоретически критическое число Рейнольдса с опытным его значением. Совпадение этих чисел будет существенным доводом в пользу концепции гидродинамической неустойчивости. ТЕОРИЯ. НЕВЯЗКИЙ ПОДХОД Теория, о которой говорилось в конце предыдущего раздела, в настоящее время существует. Она мало приспособлена для популярного изложения, так как математически весьма сложна. Скажем лишь об одном специфическом моменте. Эта теория умеет следить за развитием только малых возмущений. Это означает, что если в условиях неустойчивости возмущение растет, то скоро оно перестанет быть малым и выйдет за пределы компетенции теории. Тем не менее начальная тенденция (рост) будет отслежена этой теорией. Мы не ставим здесь перед собой цель изложить эту теорию по причине, как уже сказано, ее математической сложности. Но можно попробовать проследить за идейными моментами ее эволюции. В этом заключается наша цель. Пожалуй, следует начать с невязкого подхода, предложенного Рэлеем. Суть его заключается в том, чтобы описывать поведение во времени возникающих в потоке возмущений, не учитывая действия на возмущения вязкости. Вязкость, с одной стороны, представляет собой эффект малый, с другой - все самые интересные явления в теории гидродинамической устойчивости - рост возмущений, возникновение неустойчивости - происходят при больших числах Рейнольдса, то есть, как видно из формулы (2), это эквивалентно малой вязкости. Во всяком случае такой подход представляется в качестве первого шага разумным. К тому же существенно упрощается математический анализ. Благодаря простоте анализа Рэлею удалось установить общие теоремы, которые позволяют судить об устойчивости течения по виду его профиля скорости. Важнейшее значение среди результатов Рэлея имеет теорема о точке перегиба на профиле скорости. Согласно этой теореме, необходимым условием появления неустойчивости течения в канале является наличие точки перегиба, то есть такой точки, в которой обращается в нуль вторая производная по поперечной координате. Поэтому, например, плоское течение Пуазейля, возникающее в плоском канале под действием перепада давления, характеризуется параболическим профилем (рис. 2) и поэтому (в невязком приближении) является устойчивым: вторая производная этого профиля ни в одной точке сечения не обращается в нуль. Течения, которые получаются деформацией профиля Пуазейля, имеют точки перегиба и потому неустойчивы (рис. 3). Этот простой и замечательный результат Рэлея послужил источником очень долго жившего в теории гидродинамической устойчивости парадокса. Люди рассуждали просто. Течение Пуазейля не имеет точки перегиба и (в невязком приближении) устойчиво. Если построить более полную теорию, учитывающую влияние вязкости на возмущение, этот вывод должен только усилиться: учитывается новый фактор - вязкость, но этот фактор, подавляющий возмущения, диссипативный. С учетом вязкости возмущения будут тем более затухать, если они затухали без учета вязкости. Получается так, что, если без вязкости следует вывод об устойчивости, дальнейший анализ не нужен, вывод и так ясен. ТЕОРИЯ ГЕЙЗЕНБЕРГА. НЕЙТРАЛЬНАЯ КРИВАЯ Между тем продолжались усилия, направленные на решение задачи о поведении возмущений в общей постановке, с учетом воздействия вязкости. Отправным пунктом для подхода В. Гейзенберга (1924 год) служил результат Рэлея, который относится к предельному случаю Re ?. Необходимо было корректно определить поправки, относящиеся к случаю больших, но не бесконечно больших значений числа Рейнольдса. Гейзенберг применил метод, который всякий раз применяется в теоретической физике, когда в задаче имеется малый параметр. В нашей задаче такой параметр есть - это обратное число Рейнольдса Решение задачи в этом случае разыскивается в виде степенного ряда по малому параметру. Гейзенбергу пришлось преодолеть огромные математические трудности на пути к результату. Достаточно сказать, что, когда этот результат был обнародован, не нашлось человека, который взял бы на себя его проверку. Однако пора перейти к самому результату Гейзенберга. Он рассмотрел возмущения, периодически зависящие от продольной координаты. Таким образом, в теории появился дополнительный параметр - длина волны возмущения l, или, что то же самое, волновое число k = 2p / l. В теории, конечно, фигурирует безразмерное волновое число. Чтобы перейти к размерному, нужно учесть, что l - тоже безразмерная длина волны, то есть отношение длины волны к характерной длине - полуширине канала h, таким образом, размерное k = 2ph / l, где l - размерная длина волны. Основной результат Гейзенберга - существование нейтральной кривой для течения Пуазейля в плоском канале. Эта нейтральная кривая приведена на рис. 4. Смысл ее таков. Каждая точка этой кривой дает критическое значение числа Рейнольдса для возмущения с данным волновым числом. Внутри петли находится область неустойчивости, за пределами петли - область устойчивости. Каждая точка на кривой, таким образом, является нейтральной (отсюда название - нейтральная кривая). Кривая имеет минимум, координаты точки минимума kкр и Reкр : kкр ї 1,02, Reкр ї 3850. В полосе Re < Reкр все возмущения (с любым k) затухают. Если Re > Reкр , существует целый интервал волновых чисел (от левого края петли до правого), соответствующих растущим возмущениям. Таким образом, Reкр является критическим значением числа Рейнольдса, в области выше Reкр течение неустойчиво. Значение kкр тоже в некотором смысле замечательно. Оно дает волновое число (то есть длину волны) возмущения, которое раньше других начнет нарастать по мере увеличения числа Рейнольдса. Справа от кривой (в области больших k, то есть коротковолновых возмущений) расположена сплошная область устойчивости - вплоть до бесконечных Re. Принято говорить, что коротковолновые возмущения гасятся вязкостью. Результаты Гейзенберга воистину замечательны: он, во-первых, показал, что течение Пуазейля становится неустойчивым при больших числах Рейнольдса; во-вторых, определил критическое число Рейнольдса, начиная с которого эта неустойчивость появляется; в-третьих, определил длину волны наиболее опасного возмущения. Во всей современной теории гидродинамической устойчивости наиболее ценится именно такого рода информация. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ СОБЫТИЙ Результаты Гейзенберга были приняты интересующейся публикой скептически. Во-первых, как уже говорилось, не нашлось человека, способного пробиться через математические трудности в целях проверки результата. Во-вторых, люди привыкли рассуждать в духе парадокса устойчивости: откуда может взяться неустойчивость с учетом вязкости, если без учета вязкости ее нет (теорема Рэлея). Гейзенберг утратил интерес к задаче и больше никогда к ней не возвращался. Его интересы сместились совсем в другую область, и он вскоре прославился тем, что сформулировал основы новой науки - квантовой механики. Такое противостояние продолжалось довольно долго, почти 20 лет. За это время появились отдельные работы по теории гидродинамической устойчивости, которые в общем не влияли на ситуацию вплоть до 1943-1944 годов, когда появилась в печати работа американского математика и механика китайского происхождения Линь Цзя-Цзяо. Линь устроил генеральную проверку теории Гейзенберга, многое в ней уточнил, многое доказал из того, что принималось по интуиции на веру, не зря с тех пор теория носит имя двух выдающихся исследователей: Гейзенберга и Линя. Основной результат Линя - теория Гейзенберга получила дальнейшее подтверждение, в частности подтвердилась нейтральная кривая (она лишь количественно сместилась). Через 10 лет, в 50-х годах, с появлением быстродействующих ЭВМ задача была сосчитана численно, и снова результаты Гейзенберга подтвердились (Л.Г. Томас). Вскоре российский математик А.Л. Крылов продолжил аналитическую линию, начатую Гейзенбергом. Он строго математически доказал существование неустойчивости при больших числах Рейнольдса. Однако были люди, для которых все это не было убедительным. В самом деле, парадокс устойчивости не раскрывался. Не было ясности в вопросе о том, каким образом вязкость может провоцировать неустойчивость и как в спектре возмущений могут появиться растущие возмущения, имеющие вязкую природу. Отрицательно влияло также отсутствие прямых экспериментальных исследований, которые могли бы подтвердить теорию Гейзенберга-Линя либо опровергнуть ее (это не исключалось). ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ ТЕОРИИ От эксперимента требуется подтвердить либо опровергнуть нейтральную кривую. Если ставить эксперимент в естественных условиях, то есть ожидать появления возмущений с различными k и измерять для них критические числа Рейнольдса, то ждать придется долго и такой эксперимент не будет убедительным. Г.Б. Шубауэр и Г.К. Скрэмстед (1947 год) предложили отказаться от ожидания естественного возбуждения возмущений с различными k и перейти к их искусственному введению в поток. В работе названных авторов использовалась узкая лента, которая вводилась в поток перпендикулярно течению и приводилась в поперечные колебания с помощью электромагнитного генератора. От ленты вниз по потоку распространялись волны, затухая или усиливаясь. Частота колебаний могла меняться так, что довольно просто устанавливался нейтральный случай, когда волны не затухали и не усиливались. Таким образом определялись длина волны и волновое число. Число же Рейнольдса было задано заранее. Таким способом удавалось поставить точку на нейтральной кривой. Таких точек набралось довольно много вблизи минимума, и критическое число Рейнольдса было определено с удовлетворительной точностью. Оно совпало с теоретическим значением. Предложенную методику, основанную на искусственном внесении в поток возмущений с заданным волновым числом, позже неоднократно использовали в работах разные исследователи. ОТНОСИТЕЛЬНО ПАРАДОКСА УСТОЙЧИВОСТИ Этот вопрос до сих пор оставался открытым. Между тем хотелось бы на интуитивном уровне ("на пальцах") понять, каким образом такой диссипативный механизм, как вязкость, может провоцировать неустойчивость. Мы попробуем ответить на этот вопрос используя феноменологические рассуждения. Рассмотрим физически малый элемент жидкости (то есть малый, но макроскопический, содержащий огромное множество молекул) и представим себе, что он испытывал смещение x из своего равновесного положения. Если m - масса этого элемента, то уравнение движения для него запишется в виде Здесь - вторая производная по времени от смещения, то есть ускорение частицы. В правой части (4), как и полагается в уравнении Ньютона, указаны силы, действующие на элемент жидкости. Их две: первая - это возвращающая сила, пропорциональная смещению с обратным знаком, g - коэффициент упругой связи элемента с точкой его равновесия; вторая - это сила трения, пропорциональная скорости с обратным знаком, a - коэффициент трения. Уравнение (4) справедливо в любой момент времени, оно описывает затухающие колебания элемента около положения равновесия, их частота есть . Легко представить, что в вязкой среде существует запаздывание в передаче действия от одной точки к другой (ретардация). При этом в упругой силе аргументом у смещения x будет не мгновенное время t, а некоторый другой аргумент, отстоящий от t на t, то есть x(t - t). Это значит, что возвращающая сила определяется не мгновенным смещением, которое есть сейчас, а тем, которое было t секунд назад. Уравнение (4) принимает вид Единственное отличие этого уравнения от (4) есть сдвинутый назад на величину t аргумент у возвращающей силы. Теперь мы можем разложить в ряд Тейлора x(t - t) по степеням малого смещения t и ограничиться в разложении двумя членами: Возвратимся к уравнению (5), подставив в него разложение (6). Будем иметь Мы вернулись, в сущности, к уравнению (4), однако с эффективным трением, роль которого играет величина a * = a - gt, то есть получаем уравнение Новый коэффициент трения a* меньше истинного a (так как g и t - величины положительные). Таким образом, мы приходим к выводу, что запаздывание (ретардация) уменьшает коэффициент трения. Более того, можно даже представить, что коэффициент трения станет отрицательным. Но отрицательный коэффициент трения означает, что уравнение (9) описывает колебания с возрастающей амплитудой, то есть неустойчивость. Таким образом, дестабилизирующая роль вязкости является следствием закона запаздывания в передаче действия в вязкой среде, а это запаздывание, как следует из приведенных феноменологических рассуждений, может изменить знак эффективного трения, то есть вызвать неустойчивость. Для гидродинамиков такое рассуждение было непривычным. Радиофизики же быстро поняли суть дела. Им хорошо знакомо, что в длинных линиях с потерями и запаздыванием могут возникать паразитные токи и волны, то есть происходит возбуждение неустойчивости. Для них гидродинамическое объяснение было хорошим примером взаимного обогащения различных, как будто бы далеких друг от друга наук. ДРУГИЕ ТИПЫ ТЕЧЕНИЯ Драматическая история, о которой говорилось в предыдущих разделах, относится к плоскому течению Пуазейля, то есть течению в плоском канале под действием перепада давления. Теория, как мы видим, оказалась вполне удовлетворительной. Через все математические трудности удалось пройти, получить численное и экспериментальное подтверждение выводам теории. К сожалению, теория пока не в таком состоянии, чтобы судить об устойчивости течения только по его виду, то есть по профилю скорости. Каждое новое течение сейчас составляет для теории новую проблему. И это несмотря на наличие эффективных численных методов, реализуемых на современных компьютерах. Еще один удачный пример применения теории к анализу устойчивости течения - так называемое течение Тейлора. Это течение возникает в цилиндрическом зазоре между коаксиальными цилиндрами, если внешний цилиндр покоится, а внутренний вращается равномерно вокруг общей оси симметрии. Течение вызывается вращением внутреннего цилиндра, к которому (из-за вязкости) прилипает жидкость. Она увлекается внутренним цилиндром и увлекает остальные слои жидкости. Течение является (при малых скоростях) чисто азимутальным - жидкость движется строго по окружностям. Обнаруживается неустойчивость этого течения при достаточной скорости вращения внутреннего цилиндра (то есть при достаточно большом значении числа Рейнольдса). Критическое значение числа Рейнольдса согласно теории зависит от геометрического параметра - отношения радиусов внешнего и внутреннего цилиндров. Само критическое значение числа Рейнольдса и его зависимость от отношения радиусов находятся в отличном согласии с экспериментом. Надо сказать и о случаях, которые сегодня следует квалифицировать как неудачи теории. Первый такой случай - так называемое течение Куэтта, то есть течение, возникающее в плоском слое между твердыми границами, которые движутся "в себе" в разные стороны с одинаковыми скоростями. Каждая граница увлекает за собой непосредственно прилегающий к ней слой жидкости, а вообще в слое возникает течение с простейшим - линейным профилем скорости. Применение теории к этому течению приводит к удручающему результату: все возмущения (малые) в этом слое при всех числах Рейнольдса затухают, наступает абсолютная устойчивость (при том, что в эксперименте отчетливо фиксируется переход к турбулентности и измеряется критическое число Рейнольдса). Таким же образом обстоит дело и в случае цилиндрического течения Пуазейля, то есть течения в круглой трубе (не в плоском канале) под действием перепада давления. Результат анализа такой же, как в случае течения Куэтта, - абсолютная устойчивость. Этот случай особенно досадный, так как с этой задачи начиналось изучение ламинарно-турбулентного перехода и всякий знает, что такое течение турбулизуется и существует критическое число Рейнольдса, при котором это происходит. В чем же дело? Ответ на этот вопрос вряд ли сможет кого-нибудь удовлетворить. Он состоит в следующем. Как уже говорилось, вся теория умеет обращаться только с малыми возмущениями. Они затухают. Но, может быть, конечные возмущения будут нарастать! Есть примеры ситуаций, когда малые возмущения затухают, а конечные нарастают (рис. 5). На рис. 5 видно, что малые возмущения будут затухать, а если величина возмущения превосходит некоторое пороговое значение, - нарастать. Но теории, учитывающей конечный уровень возмущений, сегодня не существует. ЗАКЛЮЧЕНИЕ Мы познакомились с физическим явлением, широко распространенным в природных условиях и в технике. Постарались проследить идейные этапы теории гидродинамической неустойчивости начиная со времени зарождения самой идеи и до ее современного этапа, включающего численное и экспериментальное подтверждение. Мы старались здесь не обойти стороной трудности теории, так как преодоление трудностей - столбовая дорога научного познания. К сожалению, мы не охватили один яркий пример, где соображения устойчивости играют первостепенную роль - речь идет о горячей замагниченной плазме. Как известно, через горячую замагниченную плазму лежит наш путь к управляемому термоядерному синтезу. И главным препятствием на пути к управляемому термоядерному синтезу является неустойчивость плазменных систем. Таких неустойчивостей известно около сотни. Каковы эти неустойчивости и, главное, какие пути по части их преодоления сейчас разрабатываются - все эти вопросы, очевидно, очень интересны, но это предмет особого разговора. ЛИТЕРАТУРА 1. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 736 с. 2. Джозеф Д. Устойчивость движений жидкости. М.: Мир, 1981. 638 с. 3. Шлихтинг Г. Возникновение турбулентности. М.: ИЛ, 1962. 203 с. 4. Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972. 392 с. 5. Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений. М.: Наука, 1989. 320 с. * * * Григорий Зеликович Гершуни, доктор физико-математических наук, профессор кафедры теоретической физики Пермского государственного университета. Область научных интересов: теория гидродинамической и конвективной неустойчивости. Автор двух монографий и свыше 200 статей.
Исло Рейнольдса [править] Материал из Википедии — свободной энциклопедии Число, или, правильнее, критерий Рейно́льдса ( Число Рейнольдса определяется следующим соотношением:
где § § § § § § § Для каждого вида течения существует критическое число Рейнольдса, Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается – то есть, неустойчивая турбулентность. Числу Reкр 2300 соответствует интервал 2300–10 000; для упомянутого примера с тонкими плёнками это 20–120 – 1600. Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, вводохранилищ
Поиск по сайту: |
 Механика сплошных сред
Механика сплошных сред





 . В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, её резкое вращение или колебание могут вызвать появление турбулентности.
. В последнее время показано, что это правомерно только для напорных потоков. Но удар по трубе, её резкое вращение или колебание могут вызвать появление турбулентности. ), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
 — плотность среды, кг/м3;
— плотность среды, кг/м3; — характерная скорость, м/с;
— характерная скорость, м/с;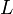 — характерный размер, м;
— характерный размер, м; — динамическая вязкость среды, Н·с/м2;
— динамическая вязкость среды, Н·с/м2; — кинематическая вязкость среды, м2/с(
— кинематическая вязкость среды, м2/с(  ) ;
) ; — объёмная скорость потока;
— объёмная скорость потока; — площадь сечения трубы.
— площадь сечения трубы. , которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При
, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При  течение происходит в ламинарном режиме, при
течение происходит в ламинарном режиме, при  возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой[источник не указан 207 дней]трубе с очень гладкими стенками
возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой[источник не указан 207 дней]трубе с очень гладкими стенками  . Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке
. Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке 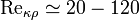 .
.