 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Особенности решения задачи АКР ⇐ ПредыдущаяСтр 9 из 9
Задача аналитического конструирования регуляторов в постановке Летова-Калмана может быть решена только численно и не имеет строгого аналитического решения в общем виде, что затрудняет анализ общих свойств синтезированных систем. Упрощение вычислительных процедур при решении задачи АКР предложено А.А.Красовским. Для этого в функционал (8.84) вводится дополнительное слагаемое, с учетом которого он принимает в развернутой форме вид
В интеграле (8.91) функция V(η) представляет собой квадратичную форму (8.86), коэффициенты которой определяются в результате решения матричного алгебраического уравнения
где В – матрица коэффициентов bik системы (2.65) размерности n х n, W – квадратная матрица весовых коэффициентов интегранта (2.91) того же размера. Уравнение (8.92) имеет единственное решение V>0, в частности, тогда, когда собственные числа матрицы В имеют отрицательные вещественные части, т.е. лишь при условии, что объект управления собственно устойчив. В этом случае синтезированная система будет асимптотически устойчива, а функция V(η) является функцией Ляпунова. Тогда алгоритм оптимального управления определяется в виде (8.87). При определении функции Ляпунова, удовлетворяющей уравнению (8.92), удобно пользоваться методом, предложенным Е.А.Барбашиным. В соответствии с этим методом искомая функция Ляпунова имеет вид матричного уравнения
где
Из уравнения (8.93) коэффициенты функции Ляпунова vik определяются по формулам Крамера
где Δ – минор, относящийся к элементу первой строки и первого столбца определителя (8.93), Δik – алгебраические дополнения элементов первой строки того же определителя, содержащих произведения ηiηk. Такое решение позволяет выразить коэффициенты vik в явном виде через коэффициенты дифференциальных уравнений возмущенного движения (8.65) bik и весовые коэффициенты функционала (8.91) wij. В результате этого алгоритм управления вида (8.90) выражается в аналитической форме через параметры объекта управления и функционала качества. Функционал (8.91) получил название критерия обобщенной работы, поскольку последнее слагаемое функционала (8.91) Все рассмотренные выше решения задачи АКР приводят к линейным регуляторам с жесткими обратными связями по координатам возмущенного движения объекта управления. Синтезированные таким образом системы управления по своей природе являются статическими и физически не в состоянии обеспечить выполнение граничных условий на концах фазовых траекторий Наряду с отмеченными негативными особенностями пристального внимания заслуживает такое структурное свойство систем управления, синтезированных в результате решения задач АКР, как устойчивость при неограниченном увеличении коэффициента усиления регуляторов. Реализация бесконечно больших коэффициентов усиления в области линейных структур связана с необходимостью иметь источник энергии неограниченной мощности, что является физически нереализуемым. Однако в работах показано, что бесконечный коэффициент усиления может быть реализован в релейных системах, работающих в скользящем режиме. В связи с этим существенным является замечание А. М. Летова о том, что выбор достаточно малого весового коэффициента с в функционалах вида (8.67) при наличии ограничения (8.66) позволяет сколь угодно близко подойти к релейной характеристике регулятора, реализующего закон оптимального управления. Действительно, при с=0 закон управления (8.90) приобретает вид
Впервые задача АКР для релейной системы была решена методом динамического программирования исходя из условия минимизации функционала
на траекториях движения системы (8.65). Оптимальное управление получено в виде
где V – функция Ляпунова (8.86), коэффициенты которой для системы (8.65) и функционала (8.95) предложено определять в результате решения основного функционального уравнения Беллмана после подстановки в него управляющего воздействия (8.96)
Строгое решение нелинейного дифференциального уравнения в частных производных (8.97) осложняется наличием в нем подсигнатурного выражения управляющего воздействия (8.96), стоящего под знаком модуля. В известных литературных источниках отсутствуют данные о методике строгого решения уравнения (8.97). Решение уравнения (8.97) может быть осуществлено исходя из условия существования в синтезированной замкнутой системе устойчивого скользящего режима, одним из условий возникновения которого является равенство нулю среднего значения сигнала на входе релейного регулятора, т.е. выполнение соотношения
С учетом (8.98) уравнение (8.97) приобретает вид
Выражение (8.99) представляет собой систему В теории оптимального управления традиционно полагают критерии оптимальности априорно заданными, оставляя выбор вида оптимизирующего функционала и его коэффициентов за пределами этой теории. Полученные в результате решения задачи АКР управления являются оптимальными лишь в смысле минимума назначенного функционала. При этом динамические свойства синтезированной системы могут не соответствовать желаемым. В связи с этим весьма актуальными являются вопросы выбора таких интегрантов оптимизирующих функционалов, при которых оптимальные системы обладали бы вполне определенными наперед заданными свойствами. Все перечисленные выше особенности задач АКР вызвали необходимость разработки новой методологии структурно-алгоритмического синтеза систем оптимального управления, устойчивых при неограниченном увеличении коэффициентов усиления регуляторов, гарантирующих желаемые динамические и статические показатели при низкой чувствительности к широкому спектру дестабилизирующих факторов и устраняющих субъективизм в назначении критериев оптимальности.
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Форми запису рівнянь елементів автоматичних систем (АС). 2. Приведення рівнянь динаміки до безрозмірної форми. 3. Операторна форма запису рівнянь динаміки АС. 4. Операційна форма запису рівнянь динаміки АС. 5. Чим відрізняюся операторна і операційна форми запису? 6. Дайте поняття стійкості АС. Проілюструйте його. 7. Траєкторії руху стійких і нестійких АС в просторі станів. 8. Необхідна і достатня умова стійкості АС. 9. Зв'язок стійкості АС с коренями характеристичного рівняння. 10. Розташування коренів характеристичного рівняння на комплексній площині. 11. Необхідна але недостатня умова стійкості АС. 12. Що таке структурна схема АС? 13. Елементи структурних схем. 14. Послідовне з’єднання динамічних ланок в структурних схемах АС. 15. Паралельне з’єднання динамічних ланок в структурних схемах .АС. 16. З’єднання динамічних ланок при зворотному зв’язку. 17. Що таке позитивний і негативний зворотні зв’язки? 18. Перенесення точки прикладання впливу на структурних схемах. 19. Перенесення вузла розгалуження на структурних схемах. 20. Перехід до одиничного зворотного зв’язку на структурних схемах. 21. Передавальна функція розімкненої системи. 22. Передавальна функція замкненої системи. 23. Передавальна функція замкненої системи за каналом помилки. 24. Передавальна функція замкненої системи за керуючим впливом. 25. Передавальна функція замкненої системи за каналом збурення. 26. Дайте поняття оптимальності систем автоматичного керування (САК). 27. Два класи задач оптимального керування. 28. Перший клас задач оптимального керування. 29. Другий клас задач оптимального керування. 30. Послідовне розв’язання задач оптимального керування першого та другого класу. 31. Фізичний сенс збуреного та незбуреного руху АС. 32. Що таке збурений, незбурений та реальний рух САК. 33. Спрощення математичного опису САК через концепцію збуреного-незбуреного руху. 34. Що таке зворотні задачі динаміки АС? 35. Розв’язання задачі синтезу замкненої системи за умови реалізації заданої передавальної функції. 36. Визначення керуючої дії на підставі принципу симетрії. 37. Сформулюйте принцип симетрії. 38. Визначення програмних керувань шляхом розв’язання зворотних задач динаміки. 39. Визначення законів керування в замкнених системах шляхом розв’язання зворотних задач динаміки. 40. Що таке модальне керування? 41. Метод стандартних коефіцієнтів при модальному керування. 42. Біноміальні стандартні форми розподілу коренів характеристичного рівняння. 43. Стандартні форми Баттерворта розподілу коренів характеристичного рівняння. 44. Стандартні форми, що забезпечують мінімум лінійної квадратичної інтегральної оцінки. 45. Узагальнена функціональна схема САК в просторі збуреного руху. 46. Що є задачею варіаційного числення? 47. Інтегральні функціонали якості. 48. Що таке функціонал? 49. Що таке варіація аргументу функціоналу? 50. Що таке приріст функції та функціоналу? 51. Що таке варіація функціоналу? 52. Рівняння Ейлера. 53. Рівняння Ейлера – Пуассона. 54. Фізичний сенс принципу максимуму. 55. Що виражає функція Гамільтона? 56. Яке значення функції Гамільтона повинне доставляти оптимальне керування? 57. Основне функціональне рівняння Беллмана. 58. Фізичний сенс функції Ляпунова. 59. Теорема Ляпунова про стійкість. 60. Теорема Ляпунова про асимптотичну стійкість.
Поиск по сайту: |
 (8.91)
(8.91) (8.92)
(8.92) (8.93)
(8.93) – выражаются через вещественные коэффициенты дифференциальных уравнений (8.65) возмущенного движения объекта управления и подчинены соотношениям:
– выражаются через вещественные коэффициенты дифференциальных уравнений (8.65) возмущенного движения объекта управления и подчинены соотношениям: ;
;

 выражает собой энергию или обобщенную работу оптимального управления Uoпт.
выражает собой энергию или обобщенную работу оптимального управления Uoпт. =0, т.е. не гарантируют сходимость интегральных функционалов качества при
=0, т.е. не гарантируют сходимость интегральных функционалов качества при  . Иными словами, не обеспечивается асимптотическая устойчивость замкнутых систем даже при отсутствии координатных возмущений. Естественное наличие внешних возмущающих воздействий усугубляет положение, т.к. кроме статической ошибки по задающему воздействию система приобретает статическую ошибку по возмущениям. Все попытки учета внешних возмущений при решении задачи АКР неизбежно приводят к комбинированному принципу управления, что влечет за собой значительное усложнение системы управления, но не дает кардинального решения проблемы вследствие практической невозможности учета и непосредственного измерения всего спектра действующих на объект возмущающих воздействий.
. Иными словами, не обеспечивается асимптотическая устойчивость замкнутых систем даже при отсутствии координатных возмущений. Естественное наличие внешних возмущающих воздействий усугубляет положение, т.к. кроме статической ошибки по задающему воздействию система приобретает статическую ошибку по возмущениям. Все попытки учета внешних возмущений при решении задачи АКР неизбежно приводят к комбинированному принципу управления, что влечет за собой значительное усложнение системы управления, но не дает кардинального решения проблемы вследствие практической невозможности учета и непосредственного измерения всего спектра действующих на объект возмущающих воздействий. (8.94)
(8.94) (8.95)
(8.95) (8.96)
(8.96) (8.97)
(8.97)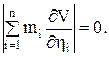 (8.98)
(8.98) (8.99)
(8.99) линейных алгебраических уравнений и в матричной форме имеет вид (8.92), т.е. является частным случаем матричного уравнения Риккати (8.89). Как указано выше, решением (8.89) является функция Ляпунова (8.93).
линейных алгебраических уравнений и в матричной форме имеет вид (8.92), т.е. является частным случаем матричного уравнения Риккати (8.89). Как указано выше, решением (8.89) является функция Ляпунова (8.93).