 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методы решения вариационных задач
Основная задача вариационного исчисления – отыскание функций, доставляющих экстремум функционалу. Ответ на этот вопрос дает уравнение Эйлера, решение которого является экстремалью. Найдем функцию, доставляющую минимум функционалу
при закрепленных граничных точках допустимых функций x(t0)=x0 и Известно, что необходимым условием экстремума является обращение в нуль вариации δI. Применим это положение к рассматриваемому функционалу (8.23). Допустим, что экстремум достигается на функции x(t). Проварьируем эту функцию и определим приращение функционала
Вариация аргумента выбрана таким образом, чтобы Разложим проварьированную функцию в ряд Тейлора
где Rn – остаток третьего и более высоких порядков малости. Член разложения (8.25) в первых фигурных скобках называется первой вариацией, она линейна. Член разложения во вторых фигурных скобках называется второй вариацией, она нелинейна. Для определения экстремума функционала необходимо исследовать линейную часть его приращения, т.е. первую вариацию. Высшими вариациями можно пренебречь. Тогда вариация функционала определяется выражением
Проинтегрируем по частям второе слагаемое в (8.26)
Первое слагаемое в полученном выражении равно нулю, так как
Интеграл (8.27) равен нулю тогда, когда равна нулю подынтегральная функция
Выражение (8.28) является уравнением Эйлера. Экстремали функционалов вида (8.23) следует искать среди решений этого уравнения. При исследовании на экстремум функционалов вида
зависящих от производных высших порядков, следует пользоваться уравнением Эйлера-Пуассона, которое приводим без вывода
Уравнения (2.28) и (2.30) составляют основу методов классического вариационного исчисления, предусматривающих непрерывность и линейность вариаций функционалов, исследуемых функций и их производных. Такая постановка вариационной задачи находит ограниченное применение в теории автоматического управления, поскольку в большинстве случаев управляющее воздействие принадлежит замкнутому множеству, т.е. ограничено по модулю. Кроме того, для реальных объектов управления подлежат ограничению некоторые фазовые координаты. Довольно часто экстремальное значение принятого критерия оптимальности достигается на разрывных управлениях. Точки разрыва могут иметь и производные оптимальных траекторий. Положение и число точек разрыва при этом заранее неизвестны. Отмеченные обстоятельства вызвали необходимость разработки современных методов вариационного исчисления, лишенных указанных недостатков. К числу таких методов относится принцип максимума Л. С. Понтрягина, доказательство которого базируется на теории множеств и функциональном анализе, которые не изучаются в курсах математики вузов. Поэтому приведем здесь упрощенное доказательство, уделив основное внимание физическому смыслу принципа не в ущерб строгости доказательства. Рассмотрим объект управления, возмущенное движение которого задано уравнениями
а цель управления - минимизация функционала
Введем новую координату
Тогда
Присоединим уравнение (8.34) к системе (8.31) и рассмотрим движение объекта управления в расширенном фазовом пространстве размерности n+1
Рис. 8.4. Наложение игольчатой Рис. 8.5. Вариация оптимальной вариации траектории
Запишем систему (8.35) в векторной форме
Здесь Будем считать, что функции f непрерывны и дифференцируемы по переменным. Задачу управления сформулируем следующим образом. Среди кусочно-непрерывных функций, удовлетворяющих условию
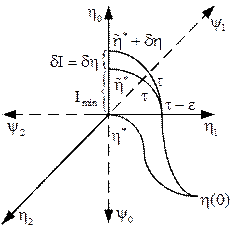
необходимо найти оптимальное управление U*, обеспечивающее минимум функционала (8.32) на траекториях движения η* системы (8.34) из любого начального положения η(0) в начало координат η = 0. Допустим, что функции η* и U* известны. Рассмотрим изменение оптимального управления во времени (рис. 8.4). Проварьируем U* на бесконечно малом интервале ε, наложив на него игольчатую вариацию δU. Величина вариации должна быть такой, чтобы проварьированное управление Игольчатая вариация, существенно отличающаяся от гладкой вариации, применяемой в классическом вариационном исчислении, позволяет расширить класс допустимых функций и является исходным положением принципа максимума. Поскольку до момента времени
Вариация
Отбросив слагаемое Rn порядка малости больше двух и учитывая (2.35), получим уравнения в вариациях
Среди всех решений уравнений (8.39) наибольший интерес представляет значение координаты
Введем вектор
Как известно, скалярное произведение двух ненулевых векторов равно нулю тогда, когда эти векторы взаимно перпендикулярны. Поэтому для выполнения соотношения (8.41) достаточно, чтобы проекции векторов δηi и ψi (i = 1, ... ,n) были взаимно перпендикулярны, а проекции Скалярное произведение (8.41) при любых неоптимальных управлениях будет отрицательно. Лишь при оптимальном управлении U* оно обращается в нуль, достигая своего максимума. В этом заключается основная идея принципа максимума. Игольчатая вариация управления прекратилась при
откуда следует
или
Представим равенство (2.42) в развернутом виде
и подставим в него значения производных из выражения (8.39)
Изменив порядок суммирования по i и j в первом слагаемом выражения (8.43), получим
откуда следует
Линейные дифференциальные уравнения (8.44) являются сопряженными основной системе (8.39). Рассмотрим неравенство (8.44) после подстановки в него значения
а также функцию Гамильтона
Из выражения (8.45) следует, что оптимальное управление должно доставлять максимальное значение функции Н. В этом заключается принцип максимума, основные положения которого достаточно наглядно представляются графически для системы второго порядка (рис. 8.5). В плоскости двух координат (η1, η2) траектория движения системы под действием оптимального управления начинается в точке начальных возмущений η(0) и заканчивается в начале координат. В пространстве трех координат (η1, η2, η0) оптимальная траектория
Следовательно, оптимальное управление обращает неравенство (8.46) в тождество, т.е. доставляет максимальное значение произведению
Во многих случаях не представляется возможным найти из условия (8.47) явный вид оптимального управления. Тогда уравнения (8.31), (8.34), сопряженная система (8.44) и условия максимума (8.47) образуют краевую задачу принципа максимума. Эта задача имеет ряд специфических особенностей, затрудняющих применение стандартных численных методов решения краевых задач. К числу таких особенностей, относятся разрывы функций U1,...,Ur, удовлетворяющих условию максимума (8.47), их неединственность, нелинейный характер зависимости Весьма общий метод решения задач оптимального управления, получивший название динамического программирования, предложен Р.Беллманом. Рассмотрим основные положения этого метода. Начнем с решения задачи об оптимальном по быстродействию переходе объекта управления (8.31) из фазового состояния η0 в начало координат η=0. Предположим, что траектория такого перехода существует для любых начальных возмущений и движение по ней происходит за минимальное время под действием допустимых управлений U. Время, в течение которого осуществляется движение по оптимальной траектории, обозначим через Т. Для простоты рассмотрим движение объекта управления второго порядка из произвольной начальной точки η(0) в начало координат. Допустим, что в течение некоторого времени t1–t0 объект управления двигался из точки η(0) в точку η1 под действием произвольного постоянного управления U=U0 по неоптимальной траектории 1 (рис. 8.6). Начиная с точки η1 объект переведен на оптимальную траекторию 2. Время Т движения по оптимальной траектории зависит от положения начальной точки η1 перехода с траектории 1 на траекторию 2, т.е. является функцией фазовых координат системы
Рис. 8.6. Фазовая траектория
Функция (8.48) непрерывна и всюду, кроме начала координат, имеет непрерывные частные производные по координатам рассматриваемого фазового пространства. Двигаясь по оптимальной траектории, объект затратит на перемещение из точки η1 в начало координат время Следовательно,
Разделив обе части неравенства (8.49) на положительную длительность интервала t1–t0, получим
Перейдем к пределу при
Производная (8.50) вычисляется по формуле полной производной в силу системы (8.31)
Тогда
Очевидно, что неравенство (8.52) превращается в тождество лишь при оптимальном по быстродействию управлении. Иными словами, оптимальное управление доставляет максимум производной (8.51), которая физически представляет собой скорость убывания времени переходного процесса, т.е.
или
Рассмотрим теперь общую задачу управления, оптимального в смысле минимума интегрального функционала
Задача оптимального управления объектом (8.31) формулируется следующим образом. Требуется из всех допустимых управлений, переводящих изображающую точку из положения η(0) в начало координат, выбрать такое, которое придает функционалу (8.54) наименьшее значение. Следует отметить, что если Предположим, что Введем на каждой траектории новое время τ, связанное с временем переходного процесса дифференциальной зависимостью
В новом времени функционал (2.54) преобразуется к виду
а поставленная задача сводится к рассмотренной ранее задаче оптимального быстродействия. Пусть U – управление, переводящее изображающую точку из положения η(0) в положение η1, a η(t) – соответствующая траектория. Положим
Функция τ(t) является непрерывной и монотонно возрастающей, так как
Тогда
Следовательно, в новой временной области объект управления (8.31) описывается системой дифференциальных уравнений
Подставив (8.56) в (8.51) и далее в (8.53), получим
или
Для определения оптимального управления U*, доставляющего минимум (8.57), необходимо найти производную
и решить совместно (8.57) и (8.58). Выражение (8.57) называется основным функциональным уравнением Беллмана, a S(η) – функцией Беллмана.
Прямой метод Ляпунова Одним из наиболее эффективных методов исследования устойчивости движения является прямой метод Ляпунова, который часто называют вторым методом Ляпунова. Для раскрытия сути этого метода рассмотрим некоторые вещественные функции
где μ – постоянное положительное число. Предполагается, что в области (8.59) эти функции однозначны, непрерывны и обращаются в нуль, когда все
Если в окрестностях начала координат функция V кроме нуля может принимать значения только одного знака, то она называется знакопостоянной (соответственно положительной или отрицательной). Если же знакопостоянная функция обращается в нуль только в начале координат, то функция V называется знакоопределенной (соответственно положительно-определенной или отрицательно-определенной). Такие функции V используются для исследования устойчивости движения и называются функциями Ляпунова. Знакоопределенная функция при Предположим, что положительно-определенная функция V=V(η) непрерывна вместе с производными первого порядка. Тогда при
Разложим функцию V(η) в ряд Маклорена по степеням
где Rn – члены разложения высшего порядка. Учитывая соотношения (8.60) и (8.61), получим
Здесь постоянные числа
Из выражения (8.62) видно, что разложение положительно-определенной функции V в ряд Маклорена по степеням Таким образом, вне зависимости от членов высшего порядка при достаточно малых по модулю значениях ηi функция V будет положительно-определенной, если положительно-определенной является квадратичная форма
Именно поэтому в теории управления поиск функций Ляпунова чаще всего осуществляется в классе квадратичных функций вида (8.63). Для определения положительной определенности квадратичных форм (8.63) используют критерий Сильвестра, в соответствии с которым квадратичная форма является положительно-определенной, если все главные диагональные миноры матрицы ее коэффициентов vik положительны. В основу прямого метода Ляпунова положены две теоремы. 1. Теорема Ляпунова об устойчивости движения. Если для дифференциальных уравнений возмущенного движения (8.9) можно найти положительно-определенную функцию V, полная производная по времени которой в силу этих уравнений была бы отрицательной знакопостоянной функцией, то невозмущенное движение устойчиво. 2. Теорема Ляпунова об асимптотической устойчивости. Если для дифференциальных уравнений возмущенного движения (8.9) можно найти положительно-определенную функцию V, полная производная по времени которой в силу этих уравнений была бы отрицательно-определенной функцией, то невозмущенное движение асимптотически устойчиво. Физически функцию Ляпунова можно отождествлять с избыточной энергией, запасенной системой на траекториях возмущенного движения, по сравнению с запасом энергии на траекториях невозмущенного движения. Если избыточная энергия системы постоянно убывает, о чем свидетельствует отрицательность производной функции Ляпунова, то убывают силы, вызывающие отклонение истинного движения от невозмущенного. При этом исследуемая система возвращается на траектории невозмущенного движения вне зависимости от того, чем были вызваны начальные отклонения. Покажем теперь условия соответствия основного функционального уравнения Беллмана прямому методу Ляпунова. Рассмотрим уравнения (8.31) и функционал (8.32). Будем считать, что существует положительно-определенная функция Ляпунова V(η), а интегрант функционала (8.32)
или
Таким образом, если в качестве интегранта критерия оптимальности принята положительно-определенная или неотрицательная функция, в процессе решения вариационных задач функция Беллмана однозначно может быть заменена функцией Ляпунова. Это следует из сопоставления выражений (8.57) и (8.64).
Поиск по сайту: |

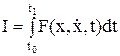 (8.23)
(8.23) . Функция
. Функция 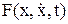 предполагается непрерывной и дважды дифференцируемой по всем аргументам. Геометрическая трактовка задачи приведена на рис. 8.3. Необходимо найти уравнение такой линии, проходящей через граничные точки x(t0) и x(t1), которое, будучи подставленным в (8.23), доставляло бы I минимальное значение.
предполагается непрерывной и дважды дифференцируемой по всем аргументам. Геометрическая трактовка задачи приведена на рис. 8.3. Необходимо найти уравнение такой линии, проходящей через граничные точки x(t0) и x(t1), которое, будучи подставленным в (8.23), доставляло бы I минимальное значение. . (8.24)
. (8.24) , т.е. варьируемая линия, описываемая функцией
, т.е. варьируемая линия, описываемая функцией  , проходила через точки x(t0) и x(t1).
, проходила через точки x(t0) и x(t1).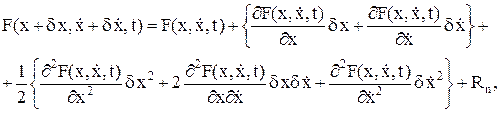 (8.25)
(8.25) . (8.26)
. (8.26)
 по условию задачи. С учетом этого выражение вариации функционала примет вид:
по условию задачи. С учетом этого выражение вариации функционала примет вид: (8.27)
(8.27) . (8.28)
. (8.28) , (8.29)
, (8.29)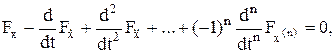 (8.30)
(8.30) – частные производные интегранта функционала (8.29) по производным переменной х от 0 до n-го порядка.
– частные производные интегранта функционала (8.29) по производным переменной х от 0 до n-го порядка.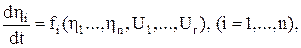 (8.31)
(8.31) (8.32)
(8.32) (8.33)
(8.33) (8.34)
(8.34) . (8.35)
. (8.35)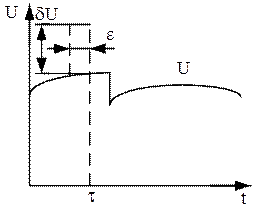
 . (8.36)
. (8.36) – вектор в (n+1)-мерном пространстве в отличие от вектора η в n-мерном.
– вектор в (n+1)-мерном пространстве в отличие от вектора η в n-мерном. , (8.37)
, (8.37)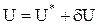 удовлетворяло условию (8.37), т.е. не превышало заданных ограничений. Поскольку длительность ε игольчатой вариации бесконечно мала, даже большие значения δU оказывают бесконечно малое влияние на последующее движение объекта управления.
удовлетворяло условию (8.37), т.е. не превышало заданных ограничений. Поскольку длительность ε игольчатой вариации бесконечно мала, даже большие значения δU оказывают бесконечно малое влияние на последующее движение объекта управления. к объекту прикладывалось оптимальное управление, он двигался по оптимальной траектории
к объекту прикладывалось оптимальное управление, он двигался по оптимальной траектории  . В результате варьирования управления на интервале
. В результате варьирования управления на интервале  дальнейшее движение
дальнейшее движение  отличается от оптимального
отличается от оптимального  . Величину
. Величину  в момент времени
в момент времени  можно определить как произведение разности скоростей изменения
можно определить как произведение разности скоростей изменения  на длительность ε игольчатой вариации
на длительность ε игольчатой вариации . (8.38)
. (8.38) (j=0,l, ... ,n) и разложения в ряд Тейлора по δηj:
(j=0,l, ... ,n) и разложения в ряд Тейлора по δηj: (j = 0,l, ... ,n).
(j = 0,l, ... ,n).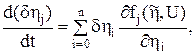 (j = 0,l, ... ,n). (8.39)
(j = 0,l, ... ,n). (8.39)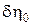 в любой момент времени t,
в любой момент времени t,  . Такой интерес вполне понятен, так как
. Такой интерес вполне понятен, так как  . (8.40)
. (8.40) такой, чтобы скалярное произведение
такой, чтобы скалярное произведение  было равно
было равно  , т.е.
, т.е. . (8.41)
. (8.41)
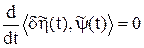 ;
;  ,
,

 . (8.43)
. (8.43)
 (i = 0,1, …, n) . (8.44)
(i = 0,1, …, n) . (8.44) (8.45)
(8.45)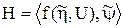 .
. происходит вариация
происходит вариация  , которая отсекает на оси η0 после окончания переходного процесса отрезок
, которая отсекает на оси η0 после окончания переходного процесса отрезок  . Из расположения осей координат сопряженной системы
. Из расположения осей координат сопряженной системы  следует, что скалярное произведение векторов
следует, что скалярное произведение векторов  определяется соотношением
определяется соотношением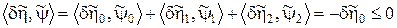 . (8.46)
. (8.46)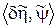 , и может быть определено из условия максимума функции Гамильтона
, и может быть определено из условия максимума функции Гамильтона (8.47)
(8.47) при соблюдении уcловия (8.37) даже в линейных системах. Кроме того, особенностью решения оптимизационных задач, связанных с принципом максимума даже в случаях, когда удается найти явный вид оптимальных управлений, является их плохая сходимость, вызванная неустойчивостью совместного решения систем (8.31) и (8.44).
при соблюдении уcловия (8.37) даже в линейных системах. Кроме того, особенностью решения оптимизационных задач, связанных с принципом максимума даже в случаях, когда удается найти явный вид оптимальных управлений, является их плохая сходимость, вызванная неустойчивостью совместного решения систем (8.31) и (8.44). . (8.48)
. (8.48)
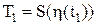 . В результате переход из точки η(0) в начало координат по траекториям 1 и 2 совершится за время
. В результате переход из точки η(0) в начало координат по траекториям 1 и 2 совершится за время  . Если бы движение из точки η(0) сразу осуществлялось по оптимальной траектории 2, то объект управления был бы переведен в начало координат за минимальное время:
. Если бы движение из точки η(0) сразу осуществлялось по оптимальной траектории 2, то объект управления был бы переведен в начало координат за минимальное время:  .
.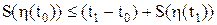 . (8.49)
. (8.49) .
. :
: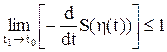 . (8.50)
. (8.50) . (8.51)
. (8.51)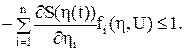 (8.52)
(8.52)
 (8.53)
(8.53) (8.54)
(8.54) , функционал (8.54) примет вид
, функционал (8.54) примет вид  . Следовательно, задача оптимального быстродействия является частным случаем рассматриваемой общей задачи.
. Следовательно, задача оптимального быстродействия является частным случаем рассматриваемой общей задачи. . Это условие выполняется для всех интегральных квадратичных функционалов.
. Это условие выполняется для всех интегральных квадратичных функционалов.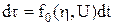 .
. ,
, . (8.55)
. (8.55) . Поэтому существует обратная к ней функция t(τ). Из (8.55) получим
. Поэтому существует обратная к ней функция t(τ). Из (8.55) получим .
.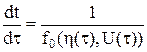 .
. . (8.56)
. (8.56) ,
, . (8.57)
. (8.57) (8.58)
(8.58) , определенные в области
, определенные в области (8.59)
(8.59)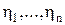 равны нулю, то есть
равны нулю, то есть . (8.60)
. (8.60)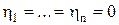 имеет экстремум (минимум для положительно-определенной функции и максимум для отрицательно-определенной функции). Знакопостоянные функции в начале координат экстремума не имеют.
имеет экстремум (минимум для положительно-определенной функции и максимум для отрицательно-определенной функции). Знакопостоянные функции в начале координат экстремума не имеют. . (8.61)
. (8.61) ,
, . (8.62)
. (8.62) определяются выражением
определяются выражением .
. . (8.63)
. (8.63) положительная знакопостоянная или положительно-определенная функция. Тогда в соответствии с приведенными теоремами Ляпунова замкнутая система управления, оптимальная в смысле минимума функционала (8.32), будет устойчива, если выполняются условия
положительная знакопостоянная или положительно-определенная функция. Тогда в соответствии с приведенными теоремами Ляпунова замкнутая система управления, оптимальная в смысле минимума функционала (8.32), будет устойчива, если выполняются условия
 (8.64)
(8.64)