 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Форми запису рівнянь елементів автоматичної системиСтр 1 из 9Следующая ⇒
СУЧАСНІ МЕТОДИ СИНТЕЗУ СИСТЕМ КЕРУВАННЯ Змінні величини і коефіцієнти, що входять в рівняння, мають певну розмірність. Для зручності частіше використовують безрозмірну форму запису, для чого кожну змінну помножують та ділять на базове значення (звичайно номінальне усталене значення). Розглянемо диференційне рівняння динаміки двигуна постійного струму
Поділимо ліву та праву частину рівняння на ωн.
Приведення рівнянь до безрозмірної форми у відносних одиницях називають спрямованим нормуванням. Зручна операторна форма запису, коли безрозмірні одиниці позначують х1, х2,… хі або у1, у2,… уі; вводять символи операторів диференціювання
а коефіцієнти позначують аі та bi, тоді диференційне рівняння
можливо записати у вигляді
Застосовують зовні схожу, але принципово іншу форму, яка має назву операційна. Якщо до змінної x(t) застосувати перетворення Лапласа, то отримують зображення цієї функції x(p)
При цьому перша похідна від х буде мати зображення рх(р), друга р2х(р), третя р3x(р) і т.д. Інтеграл від х буде мати зображення
Розв’язавши операційне рівняння, ми знайдемо не оригінал х(t), а тільки його зображення х(р). Визначити оригінал по зображенню можна або за допомогою таблиці оригіналів і їх зображень, або застосувавши зворотне перетворення Лапласа Рівняння одного і того ж елемента, записані в операторній і операційній формі, зовні зовсім однакові. Однак, вони принципово відрізняються один від одного. Рівняння (1) є диференціальним, в ньому буква р позначає оператор диференціювання
Поиск по сайту: |
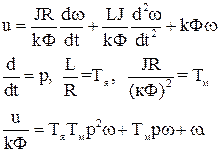
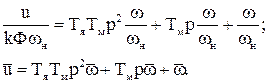
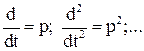
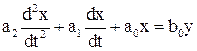
(1)
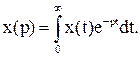
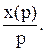Якщо застосувати перетворення Лапласа до диференціального рівняння (1), то при нульових початкових умовах воно набуде вигляду
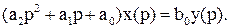(2)
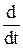, а змінні х(t) та y(t) є реальними функціями часу. Рівняння ж (2) - алгебраїчне, в ньому р є незалежною комплексною змінною, а величини х(р) і у(р) є тільки зображеннями фізичних величин х(t) та y(t). Формально від операторної до операційної формі можна перейти шляхом заміни позначень змінних як функцій часу t позначеннями цих змінних як функцій комплексної змінної р. Але це можна робити тільки в тому випадку, якщо початкові умови для диференціального рівняння нульові. В іншому випадку в операційному алгебраїчному рівнянні з'являться додаткові члени, що враховують початкові умови.