 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойство симметрии систем автоматического управления
Проблема синтеза систем автоматического управления с требуемыми динамическими свойствами в той или иной мере связана с концепциями обратных задач динамики, в результате решения которых по заданному закону движения системы определяются силы или управляющие воздействия, под действием которых это движение осуществляется. В самом широком понимании содержание обратных задач динамики включает определение законов управления движением динамических систем и их параметров из условия воспроизведения назначенных траекторий. Определение законов управлений движением динамических систем составляет содержание структурно-алгоритмического синтеза САУ. С другой стороны, определение параметров динамической системы является задачей параметрического синтеза, когда структура системы управления предполагается известной априори. Обе эти задачи составляют основу теории автоматического управления. Несмотря на то, что обратные задачи динамики имеют давнюю и богатую историю, в настоящее время они приобретают все более широкое понимание и толкование. В частности, за последнее десятилетие ими завоеваны прочные позиции в теории автоматического управления (ТАУ). Существо таких задач заключается в построении замкнутых САУ, осуществляющих движение по назначенным траекториям (траекториям невозмущенного движения) с помощью законов управления с обратными связями по переменным состояния управляемых объектов. В процессе развития классической и современной ТАУ вне зависимости от достижений в области решений обратных задач динамики разработано множество практических приемов и методов создания и расчета САУ различной природы и назначения. К ним в первую очередь следует отнести частотные и корневые методы, а также задачи аналитического конструирования оптимальных регуляторов по минимуму интегральных функционалов качества, рассмотренные в первой главе. В любой постановке проблемы синтеза с использованием перечисленных методов конечной целью является определение таких структур и параметров САУ, при которых процессы динамики систем протекают по предписанным законам или максимально приближаются к процессам, протекающим в некоторой эталонной модели, в наибольшей степени отвечающей требованиям технического задания на проектирование. Аналогичная цель преследуется решениями обратных задач динамики. Это позволяет сделать вывод о том, что методы синтеза САУ, применяемые в теории автоматического управления, прямо или косвенно связаны с концепциями обратных задач динамики. В каждом из них в явном виде или косвенно задана эталонная модель невозмущенного движения и требуется определить закон управления в функции переменных состояния управляемого объекта, обеспечивающий движение изображающей точки по заданным траекториям. Рассмотрим классическую задачу теории автоматического управления, содержанием которой является определение структуры и параметров закона управления. По известной передаточной функции объекта управления W(p) требуется найти передаточную функцию управляющего устройства Wy(p) такую, чтобы замкнутая система автоматического управления обладала желаемой передаточной функцией Ф*(р). В такой постановке задачи желаемая траектория движения или требуемые динамические свойства синтезируемой системы заданы видом передаточной функции Ф*(р). Искомым является закон управления, заданный в виде передаточной функции управляющего устройства Wy(p). Совокупность объекта управления и управляющего устройства образует замкнутую САУ. Определение закона управления и его параметров в виде передаточной функции Wy(p) при располагаемых исходных данных соответствует содержанию обратных задач динамики. Структурная схема синтезируемой системы приведена на следующем рисунке
Передаточная функция замкнутой системы
Подставив вместо Ф(р) заданную передаточную функцию замкнутой системы Ф*(р) и разрешив полученное уравнение относительно Wy(p), найдем искомый закон управления в виде передаточной функции
Выражение (7) формально решает задачу синтеза замкнутой системы из условия реализации заданной передаточной функции. Это свидетельствует о том, что традиционная задача теории автоматического управления формулируется и решается как обратная задача динамики в ее непосредственном понимании. Желаемая траектория движения синтезированной системы задается в виде передаточной функции Ф*(р) некоторой эталонной модели, а искомый закон управления определяется также в виде передаточной функции Wy(p) или уравнением U(p)=Wy(p)[y*(p) - у(р)]. Рассмотрим синтез системы управления, обеспечивающей движение изображающей точки по назначенной траектории, как решение обратной задачи динамики в иной постановке. Пусть движение управляемого объекта подчиняется дифференциальным уравнениям
Система n уравнений (8) может быть приведена к одному дифференциальному уравнению n-го порядка
Требуется определить управляющее воздействие u, которое обеспечит движение координат у1(t) по траектории у1*(t). В соответствии с основной идеей обратных задач динамики определим управляющее воздействие из уравнения (9)
Подставим в (10) вместо текущего значения переменной y1(t) ее желаемое значение y1*(t)
Из выражения (11) следует, что искомое управляющее воздействие может быть найдено как функция времени в результате выполнения конечного числа операций: дифференцирования, сложения, умножения и т.д. На основании соотношения (11) формулируются общие положения определения управляющих воздействий, обеспечивающих движение системы по назначенной траектории. Из сопоставления выражений (9) и (11) следует, что операции формирования искомого управления обратны соответствующим операциям, определяющим структуру математической модели управляемого объекта. Интегрированию в математической модели объекта соответствует дифференцирование в алгоритме управления, суммированию соответствует вычитание, умножению – деление. В конечном итоге выходная u* и входная y1* переменные структурной схемы алгоритма управления представляют собой соответствующие обращенные переменные u, y1 математической модели управляемого объекта. Таким образом, структурная схема управляющей части системы может быть получена на основании структурной схемы объекта управления в результате обращения операций и соответствующих переменных. На рис.1 приведена структурная схема системы управления, построенная в соответствии с уравнениями (9) и (10) при n=2.
Входной переменной схемы является траектория невозмущенного движения y1*, а выходной – фактическая переменная y1. Если выполнить обращение соответствующих операций и переменных, то изменится направленность схемы, т.е. выход системы станет ее входом и наоборот, а общая конфигурация структурной схемы не изменится. В результате такого обращения структурная схема примет вид, изображенный на рис. 2.
Рис. 2. Структурная схема обращенной системы
Таким образом, можно сформулировать следующее правило: алгоритм формирования управляющего воздействия строится по принципу симметрии структуры и обращения операций по отношению к структуре и группе операций, соответствующих математической модели управляемого процесса. Приведенные структурные схемы наглядно иллюстрируют свойства симметрии, присущие системам автоматического управления. Эти свойства однозначно определяют структуру и параметры управляющей части системы и составляют методологическую основу для отыскания алгоритмов управления движением динамических объектов по назначенной траектории. При этом задача конструирования алгоритмов управления полностью соответствует концепциям обратных задач динамики и сводится к отысканию управляющей функции u* , обеспечивающей движение объекта по предписанной траектории уi*. В рассмотренной постановке решение обратной задачи динамики дает возможность определения программных управлений, обеспечивающих системе наперед заданные динамические свойства, если предписанную траекторию движения задать уравнением py1*(t)= где xi(t) – известные функции времени; сi – постоянные, однозначно определяющие начальное состояние системы. Путем подстановки выражения (12) в (11) определим искомое программное управление u*(t)=m-1[c1 Весьма существенным является то, что управления вида (13) обеспечивают реализацию только таких траекторий движения, структура которых как функций времени отвечает структуре решения уравнения (9) при u=0. Отсюда следует вывод, что программные управления реализуются лишь при соблюдении условий воспроизводимости назначенных траекторий. Более предпочтительной является реализация назначенных траекторий движения в замкнутых системах на основании законов управления с обратными связями. Для отыскания таких законов необходимо выразить функции времени сi pkxi(t)= Если xi(t) в выражении предписанной траектории (12) соответствует условию (14), то программное управление (13) принимает вид u*(t)=m-1 где коэффициенты γi, определяются выражениями γi = Для построения закона управления с обратными связями на основе программного управления (15) необходимо выразить функции cixi(t) через переменные состояния системы (9). Такими переменными являются pkyi(t), (k=0,l,..., n-1). Тогда в соответствии с условием воспроизводимости назначенной траектории движения yi(t)=yi*(t) можно получить следующее выражение
Решив систему уравнений (16) относительно искомых переменных cixi(t), определим
где βik – постоянные коэффициенты. Подставив выражения (17) в (15), получим закон управления с обратной связью
Траектория невозмущенного движения y*(t), заданная уравнением (12), реализуется в замкнутой системе с алгоритмом управления (18), в котором коэффициенты обратных связей по переменным yi, pyi,…,pn-1yi определяются выражением
Таким образом, в результате решения обратной задачи динамики на основе принципа симметрии получен алгоритм управления замкнутой системы в аналитическом виде как функция переменных состояния и параметров объекта управления, а также известных функций времени, определяющих вид предписанной траектории движения с учетом начального состояния системы. Модальне керування Переміщення всіх коренів (полюсів) замкнутої системи в будь яке наперед задане положення становить предмет теорії модального керування. Походження терміна "модальне керування" пояснюється тим, що кожному кореню відповідає певна складова вільного руху системи, звана модою. При використанні методів модального керування насамперед виникає питання про розташування коренів системи, до якого слід прагнути. Це питання в кожному конкретному випадку може вирішуватися по різному, в залежності від властивостей об'єкта керування та інших обставин. Розглянемо тільки один метод, що дає рекомендації по розташуванню коренів системи і повністю справедливий у випадку, якщо передавальна функція замкнутої системи не має нулів. Необхідно відзначити, що і в разі наявності нулів виконання рекомендацій методу стандартних коефіцієнтів, що викладається нижче, дає рішення, близькі до оптимальних в розглянутому сенсі.
Поиск по сайту: |

 .
.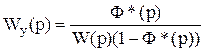 . (7)
. (7) , (i=1,…,n). (8)
, (i=1,…,n). (8) . (9)
. (9) . (10)
. (10) . (11)
. (11)
 Рис. 1. Структурная схема системы
Рис. 1. Структурная схема системы
 , (12)
, (12) +...+сn
+...+сn  ]. (13)
]. (13) (t) через переменные состояния управляемого объекта. Такая задача легко решается для функций xi(t), подчиненных соотношению
(t) через переменные состояния управляемого объекта. Такая задача легко решается для функций xi(t), подчиненных соотношению ,(k=0,l,...,n) . (14)
,(k=0,l,...,n) . (14) , (15)
, (15)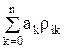 , (i=1,...,n) .
, (i=1,...,n) . (k=0,1,…n-1) (16)
(k=0,1,…n-1) (16)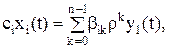 (i=1,…,n) , (17)
(i=1,…,n) , (17) (18)
(18) (k=0,1,…,n-1). (19)
(k=0,1,…,n-1). (19)