 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Концепция возмущенного - невозмущенного движения
Необходимость учета различной физической природы объектов, входящих в состав высокотехнологичных процессов и комплексов, значительно усложняет математическое описание системы управления. Избежать этого возможно, если вместо реальных физических переменных использовать их относительные единицы. Переход к системе относительных единиц путем направленного нормирования позволяет оперировать переменными в безразмерной форме. Такое представление помимо технических преимуществ имеет также важное методологическое значение. Различные по физическому составу объекты описываются однотипными математическими моделями, что значительно упрощает их исследование. К таким объектам могут быть применены общие методы и принципы автоматического управления. Законы и закономерности, положенные в основу вычислительных процедур, могут быть перенесены на широкий класс объектов. Каким образом осуществляется нормирование ЭМС, будет рассмотрено в дисциплинах следующего семестра. При изложении же основ синтеза оптимальных систем будем предполагать, что такая процедура уже выполнена, и под переменными объекта в дальнейшем будут подразумеваться их относительные значения. Концепция возмущенного - невозмущенного движения и учение А. М.Ляпунова об устойчивости легли в основу большинства методов синтеза систем оптимального управления, и их основные понятия и положения используются в дальнейшем при разработке новой методологии структурно-алгоритмического синтеза систем, устойчивых при неограниченном увеличении коэффициента усиления. Рассмотрим объект управления, движение которого описывается системой дифференциальных уравнений в форме Коши
В (8.1) Решение системы (8.1) представляет собой закон движения изображающей точки у в фазовом пространстве, а путь, описываемый этой точкой, траекторией движения. Такое движение называется управляемым. Если правые части (8.1) не содержат в явном виде u, то решение системы (8.1) будет являться свободным движением. На управления и переменные состояния накладываются ограничения, выражающие ограниченные ресурсы сигналов управления и допустимые пределы изменения переменных состояния:
Среди всех траекторий движения системы (8.1) всегда можно выделить искомое движение
которое сообщается ОУ желаемым (программным) управлением
Реальное движение всегда отличается от желаемого по ряду причин: – неточное знание начальных условий функционирования объекта; – неточная информация о возмущениях, действующих на систему; – неточная реализация желаемого управления; – нестабильность параметров ОУ и т.п. При синтезе систем оптимального управления следует рассматривать только такие желаемые траектории движения, которые физически могут быть реализованы. Движение изображающей точки по физически реализуемой траектории будет устойчивым, а физически невозможным движениям соответствуют неустойчивые решения. Концепция возмущенного-невозмущенного движения связывает устойчивость решения системы (8.1) с возможностью достижения желаемой траектории движения. Реальное движение ОУ отличается от желаемого на величину отклонения
Если в системе уравнений (8.1) переменные состояния ук и управляющие воздействия uе заменить их отклонениями (8.4) и (8.5), то в новом фазовом пространстве система (8.1) запишется как
где
По терминологии Ляпунова система (8.6) называется системой дифференциальных уравнений возмущенного движения, или системой дифференциальных уравнений в отклонениях, а решение (8.2) и (8.3) – невозмущенным движением. Если функции
где
символ Исключая в (8.7) нелинейные члены, это уравнение в первом приближении можно представить в виде
В самом общем случае коэффициенты bik и mie являются известными или случайными функциями времени. Они характеризуют переменные параметры ЭМС, к которым относятся постоянные времени, и коэффициенты усиления. Если изменение этих параметров не выходит за пределы диапазона, допускающего безаварийную работу ЭМС, то при синтезе систем управления коэффициенты bik и mie могут быть приняты постоянными и соответствующими номинальным параметрам ОУ, т.к. такие изменения не приводят к нарушению устойчивости управляемого движения. Управляющее воздействие uе при дальнейшем рассмотрении принимается скалярной функцией, скалярно входящей в систему, т.е. ЭМС рассматривается как односвязный объект с одним входом, на который подается один сигнал управления. Такие оговорки обусловлены лишь исследуемым классом объектов и не связаны с ограниченными возможностями излагаемой методологии синтеза. С учетом сказанного, уравнение (8.8) принимает вид
Следует отметить, что фазовые пространства реального движения y(t), желаемого движения y*(t) и возмущенного движения η(t) имеют одинаковую размерность. Выражение (8.4) определяет перенос начала координат в точку с координатами η1=0 ;...; ηn=0. Таким образом, в соответствии с концепцией возмущенного-невозмущенного движения задача устойчивости решения
переходит в задачу устойчивости нулевого решения η1=0 ;...; ηn=0. (8.10) Сходимость движений у и у* обеспечивается стабилизирующим управлением U. Таким образом, реальное управление
состоит из желаемого u*(t) и стабилизирующего U(t) управлений. Желаемое управление u*(t) обеспечивает основное (желаемое) движение системы у*, а стабилизирующее управление U(t) парирует отклонения реального движения у от желаемого у*. Однако, такое представление управляющего воздействия в виде (8.11) носит условный характер. Рассмотрим реализацию такого управления на примере обобщенной функциональной схемы СУ (рис. 8.1), движение которой описывается уравнениями вида (8.9).
Формирователь невозмущенного движения, представляющий собой модель объекта управления с базовыми параметрами, под действием задатчика программного управления формирует траекторию невозмущенного движения у*. Программное управление u*, поступая на объект управления совместно с параметрическими zп и координатными zк возмущениями, вызывает реальное движение у, координаты которого в общем случае отличаются от координат невозмущенного движения у* на значение координат возмущенного движения η. Координаты возмущенного движения поступают на регулятор, который вырабатывает стабилизирующее управление U, обеспечивающее в свою очередь сходимость нулевого решения (8.10) системы (8.9). Из принципа действия рассмотренной СУ следует, что математические задачи синтеза оптимальных систем делятся на два класса. 1. Задачи, связанные с определением и расчетом вида оптимального переходного процесса. В результате решения этих задач отыскивается программное управление u*(t), формирующее желаемые траектории невозмущенного движения у*, как известная функция времени. Системы, удовлетворяющие решению этой задачи, называются оптимальными по режиму управления. К ним относятся и системы, оптимальные по быстродействию. 2. Задачи, в результате решения которых определяется стабилизирующее управление, обеспечивающее сходимость истинного и невозмущенного движения. Системы, синтезированные в этом случае, называются оптимальными по переходному процессу. В обоих классах задачи трактуются как двухточечная граничная проблема, которая может быть решена одним из методов вариационного исчисления. Задача второго класса известна как задача АКР и суть её состоит в определении вариационными методами управляющего воздействия, которое минимизирует функционал, характеризующий отклонение траектории истинного движения системы от желаемой. Наряду с очевидной общностью между задачами указанных классов имеется существенное различие. В процессе АКР отыскивается закон управления в его аналитической форме как некоторая функция фазовых координат исходной системы. Иными словами, осуществляется конструирование дифференциального уравнения оптимального регулятора в отличие от задач первого класса, где решением является совокупность известных функций времени, на которых основывается расчет и построение программирующих устройств. Таким образом, синтез систем оптимального управления состоит из последовательного решения задач первого и второго классов. Сначала для заданного объекта управления при существующих ограничениях отыскивается оптимальная траектория движения системы, затем путем АКР определяется дифференциальное уравнение (алгоритм управления) регулятора, гарантирующее минимальное отклонение траекторий движения ОУ от найденной оптимальной траектории. Эффективность работы систем программного управления оценивается, как правило, интегральным функционалом качества, в котором подынтегральная функция (интегрант) определяется в первую очередь физической природой объекта управления. При синтезе систем стабилизации, в состав которых входит ОУ и регулятор, критерий (показатель) качества, как правило, не связан напрямую с физической природой объекта управления, но должен учитывать инженерные требования к процессу управления (время переходного процесса от истинного движения к программному, перерегулирование при этом движении, установившуюся ошибку в процессе воспроизведения программного движения). Однако в теории оптимального управления традиционно принимают критерий качества заданным, оставляя вопросы выбора его структуры и параметров за пределами этой теории. При синтезе стабилизирующих управлений обычно используют уравнения первого приближения (8.8) в связи с тем, что стабилизирующее управление предназначено для устранения отклонений (8.4), а при малых значениях этих отклонений уравнения (8.7) и (8.8) имеют близкие решения, т.к. функции Если же требуемая траектория движения известна заранее, необходимость в решении задачи первого класса отпадает. Тогда в управляющем воздействии u выделить в явном виде компоненты u* и U не представляется возможным, да в этом и нет необходимости. Если выполнено условие (8.10), следовательно, реальное управление обеспечивает движение системы по желаемой траектории у*. В начальный момент времени t=0 состояние системы характеризуется начальными отклонениями Учение Ляпунова об устойчивости позволяет судить о свойствах траекторий возмущенного движения, не прибегая к интегрированию уравнений (8.9), и дает рекомендации по рациональному выбору структуры и параметров регулятора. Если стабилизирующее управление синтезировано исходя из условия достижимости некоторым показателем качества, характеризующим цель управления, экстремального значения и решение (8.10) при этом будет устойчивым, то это означает, что система управления сама изберет тот режим движения к желаемой траектории, который этому решению соответствует. Если решение (8.10) неустойчиво, то такой режим движения окажется физически невозможным. Вопрос выбора показателя качества при синтезе алгоритмов стабилизирующего управления будет рассмотрен ниже. Физический смысл понятий возмущенного и невозмущенного движения может быть рассмотрен на примере структурной схемы обобщенной замкнутой системы автоматического управления (рис. 8.2.).
Рис. 8.2. Обобщенная структура замкнутой системы
Объект управления с передаточной функцией Woy характеризуется n-мерным вектором у состояния, компоненты которого Концепция возмущенного-невозмущенного движения Ляпунова значительно упрощает математическое описание ОУ, т.к при синтезе алгоритмов управления из рассмотрения исключаются векторы координат невозмущенного движения у*, истинного движения у и возмущающих воздействий z. Т.е. регулятор формирует управляющее воздействие в функции отклонений Основные положения концепции возмущенного-невозмущенного движения легли в основу изложенной во второй главе новой методологии структурно-алгоритмического синтеза систем оптимального управления, устойчивых при неограниченном увеличении коэффициента усиления.
Поиск по сайту: |
 (8.1)
(8.1) – переменные состояния ОУ, совокупность которых образует n-мерный вектор состояния
– переменные состояния ОУ, совокупность которых образует n-мерный вектор состояния  ;
; 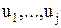 – управляющие воздействия, образующие j-мерный вектор управления
– управляющие воздействия, образующие j-мерный вектор управления  ; fk – известные функции, определенные для любых значений у и u, – непрерывные и непрерывно-дифференцируемые необходимое число раз по у, u и t. Вектор u может быть непрерывной, кусочно-непрерывной или кусочно-гладкой функцией.
; fk – известные функции, определенные для любых значений у и u, – непрерывные и непрерывно-дифференцируемые необходимое число раз по у, u и t. Вектор u может быть непрерывной, кусочно-непрерывной или кусочно-гладкой функцией.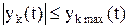 ;
; 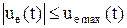 .
. , (8.2)
, (8.2) . (8.3)
. (8.3) ; (8.4)
; (8.4) (8.5)
(8.5) (8.6)
(8.6)
 разложить в ряд Тейлора в окрестности точки
разложить в ряд Тейлора в окрестности точки  ;
;  , то уравнения (8.6) примут вид
, то уравнения (8.6) примут вид (8.7)
(8.7)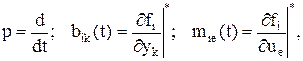
 означает, что частные производные функции f берутся в точке
означает, что частные производные функции f берутся в точке  ,
,  – функции, являющиеся членами ряда Тейлора второго и более высоких порядков малости.
– функции, являющиеся членами ряда Тейлора второго и более высоких порядков малости. . (8.8)
. (8.8) (8.9)
(8.9)
 (8.11)
(8.11)
 зависят от вторых и более высоких степеней этих отклонений. Линейный характер уравнений первого приближения позволяет существенно упростить процедуру синтеза стабилизирующих управлений.
зависят от вторых и более высоких степеней этих отклонений. Линейный характер уравнений первого приближения позволяет существенно упростить процедуру синтеза стабилизирующих управлений.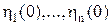 , которые могут принимать практически любые возможные для конкретного ОУ значения. Конечный момент времени
, которые могут принимать практически любые возможные для конкретного ОУ значения. Конечный момент времени  характеризуется равенством нулю всех отклонений
характеризуется равенством нулю всех отклонений 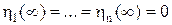 . Такому многообразию начальных условий соответствует такое же многообразие решений системы (8.9), а соответственно и семейство траекторий возмущенного движения, учесть которые полностью физически невозможно. Это значительно усложняет задачу синтеза системы управления.
. Такому многообразию начальных условий соответствует такое же многообразие решений системы (8.9), а соответственно и семейство траекторий возмущенного движения, учесть которые полностью физически невозможно. Это значительно усложняет задачу синтеза системы управления.
 однозначно определяют истинное движение объекта. Это движение происходит под воздействием векторов управляющих
однозначно определяют истинное движение объекта. Это движение происходит под воздействием векторов управляющих 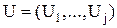 , возмущающих
, возмущающих  и задающих
и задающих 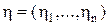 истинного движения системы
истинного движения системы