 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод стандартних коефіцієнтів.
Розглянемо замкнуту систему, що описується диференціальним рівнянням
Приймемо, що
а) біноміальні стандартні форми.
Ця пропозиція полягає в забезпеченні однаковості всіх коренів рівняння (21), причому n-кратний корінь повинен бути дійсним і негативним зі значенням модуля
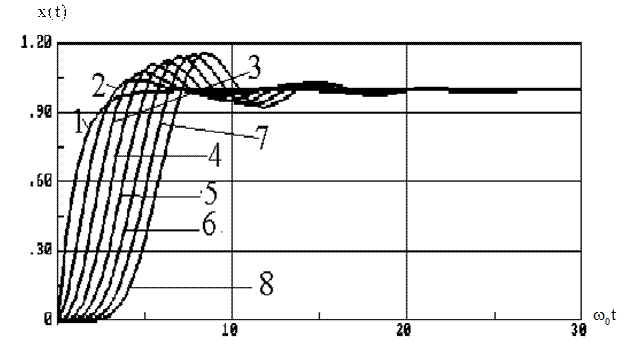
Реакції системи при біноміальному розподілі коренів є монотонними і досить повільно протікають, що в багатьох випадках не є оптимальним. На рисунку 3 наводяться реакції на одиничний ступінчастий вплив систем з біноміальним розподілом коренів від першого до восьмого порядку.
Рисунок 3. - Реакції систем з біноміальним розподілом коренів на одиничний ступінчастий вплив.
б) стандартні форми Баттерворта.
Розподіл за Баттервортом полягає в тому, що корені при дотриманні однакових кутових відстаней розподіляються по півколу радіуса
Реакції систем з розподілом коренів за Баттервортом в порівнянні з біноміальним розподілом більш коливальні, але забезпечують більшу швидкодію і в багатьох випадках відповідають інтуїтивній уяві про оптимальний перехідний процес. Реакції систем з розподілом коренів за Баттервортом з першого до восьмого порядку включно на одиничний ступінчастий вплив наведені на рисунку 4.
Рисунок 4 - Реакції систем з розподілом коренів за Баттервортом на одиничний ступінчастий вплив.
в) Стандартні форми, що забезпечують мінімум лінійної квадратичної інтегральної оцінки.
Стандартні форми в даному випадку забезпечують мінімум оцінки
і мають вигляд
Реакції системи на одиничний ступінчастий вплив в даному випадку мають більшу коливальність порівняно з розподілом за Баттервортом і наведені на рисунку 5.
Рисунок 5 - Реакції систем, оптимізованих за критерієм
г) Стандартні форми, що забезпечують мінімум інтегральної оцінки В даному випадку реакції системи на ступінчастий вплив в порівнянні з реакціями системи з біноміальним розподілом характеризуються значно більшою швидкодією, а в порівнянні з реакціями системи з розподілом за Баттервортом - істотно меншою коливальністю. Стандартні форми в цьому випадку мають вигляд:
Дані стандартні форми знаходять досить широке застосування на практиці, але будь-якого алгоритму їх визначення не існує, оскільки вони отримані експериментально. Реакції розглянутих систем на одиничний ступінчастий вплив наведені на рисунку 6.
на одиничний ступінчастий вплив
Існують рекомендації з розташування коренів на дійсній осі, що забезпечує задовільний характер перехідної функції при наявності нулів у передавальній функції. При передавальній функції з одним нулем корені рекомендується розташовувати на негативній дійсній півосі за арифметичною прогресією, а при передавальній функції з двома нулями - за геометричною. Розглянемо лінійний стаціонарний об'єкт
В сучасній теорії керування термін "об'єкт" слід розуміти більш широко, ніж зазвичай. До об'єкту будемо відносити також виконавчі органи і попередні їм підсилювачі (вхідні сигнали підсилювачів утворюють вектор U(t). До об'єкта слід відносити і чутливі елементи, приймаючи їх вихідні сигнали в якості складових вихідного вектора Будемо вважати, що всі змінні стану об'єкта підлягають безпосередньому вимірюванню і використовуються в якості вихідних сигналів. Тоді матриця С обертається в одиничну матрицю I, так що Передавальна функція об'єкта
Регулятор, що приєднується до об'єкта, отримує в даному випадку змінні стану і виробляє керування, що прикладаються до об’єкту. Будемо вважати, що регулятор лінійно перетворить сигнали, що надійшли, і видає в якості виходу їх лінійні комбінації. Вихідні сигнали регулятора можуть бути подані на об'єкт в тих же точках, що і вимірні зовнішні впливи. Позначимо ці впливи через
Знак "-" вказує на негативний зворотний зв'язок. Об'єднуючи рівняння (22) і (24), отримаємо
Перейшовши до зображень за Лапласом при нульових початкових умовах з (25) отримаємо матричну передавальну функцію замкненої системи
В практичних завданнях W матрицю R обирають так, щоб надати матриці замкнутої системи А-ВR необхідні властивості, наприклад, задане розташування власних значень. Це можливо тільки при повній керованості системи. Розглянемо випадок, коли об'єкт має тільки один вхідний сигнал. У рівнянні (22) замість вектора U(t) буде тепер скалярна величина u(t), а замість матриці В типу
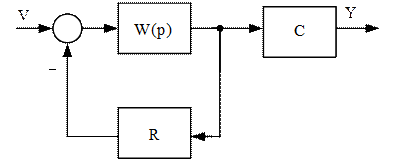
де F(p)=det(pI-A), g - матриця стовпець, отримана перемноженням приєднаної матриці і матриці b. Структурна схема замкненої системи прийме вигляд, показаний на рисунку 7.
Рисунок 7 - Структурна схема системи
Характеристичне рівняння системи
де порядок проходження матричних співмножників узятий таким, щоб добуток був скалярною величиною. Привівши ліву частину (28) до спільного знаменника і враховуючи, що чисельник дорівнює характеристичному поліному H(p) замкненої системи, отримаємо
У цьому виразі невідомою є тільки матриця-рядок r. Поліном Н(p) визначено бажаним розташуванням коренів замкненої системи і може бути обраний у вигляді однієї з стандартних форм. Прирівнюючи коефіцієнти лівої і правої частин виразу (29) при однакових ступенях оператора p, отримаємо систему алгебраїчних рівнянь, з якої можна знайти всі елементи матриці регулятора r, що забезпечують задане розташування коренів характеристичного рівняння замкненої системи.
Приклад. Розглянемо об'єкт, який описується рівняннями
Позначимо
В матричній формі можна записати
де
Чисельні значення коефіцієнтів рівнянь прийняті довільно. Матриця керованості має вигляд
Ранг цієї матриці дорівнює порядку об'єкта (n=3), об'єкт повністю керований і існує можливість побудови регулятора, що забезпечує будь-яке бажане розташування коренів замкненої системи. Поліном F(р) і матриця-стовпець g(р) визначаються з матричної передавальної функції (МПФ) об'єкта
Приймемо за бажаний характеристичний поліном біноміальну стандартну форму
Підставивши g(р), F (р), H (р) в рівняння (29), після перемноження отримаємо
Прирівнявши члени при однакових степенях р в лівій та правій частинах, отримаємо
Обираємо ω0=1 і отримаємо r1=2; r2=-1; r3=5. Враховуючи вираз (24) для системи стабілізації величини ψ, отримаємо закон керування
Розглянемо інший приклад. Синтезуємо модальний регулятор для об’єкта керування, структурна схема якого наведена на наступному рисунку
Рисунок 8. Структурна схема об’єкта керування
Система диференціальних рівнянь динаміки такого об’єкта має вигляд
Знайдемо коефіцієнти модального регулятора, рівняння якого має вигляд
Структурна схема модальної системи керування
Будемо вважати, наприклад,
звідки
8. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ВАРИАЦИОННЫХ МЕТОДОВ СИНТЕЗА СИСТЕМ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Поиск по сайту: |
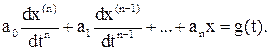 (20)
(20) , а початкові умови нульові. Щоб забезпечити в деякому сенсі "оптимальне" протікання реакції X(t), запропоновані різні розподіли коренів характеристичного рівняння
, а початкові умови нульові. Щоб забезпечити в деякому сенсі "оптимальне" протікання реакції X(t), запропоновані різні розподіли коренів характеристичного рівняння (21)
(21) , визначеним вимогами до швидкодії системи (чим більше
, визначеним вимогами до швидкодії системи (чим більше  , розгортаючи який, отримуємо стандартні (бажані) значення коефіцієнтів характеристичного рівняння. Наприклад, для систем до 8-го порядку включно характеристичний поліном має вигляд:
, розгортаючи який, отримуємо стандартні (бажані) значення коефіцієнтів характеристичного рівняння. Наприклад, для систем до 8-го порядку включно характеристичний поліном має вигляд:



 .
.
 , на одиничний ступінчастий вплив
, на одиничний ступінчастий вплив
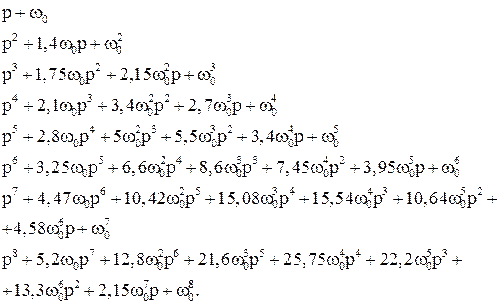
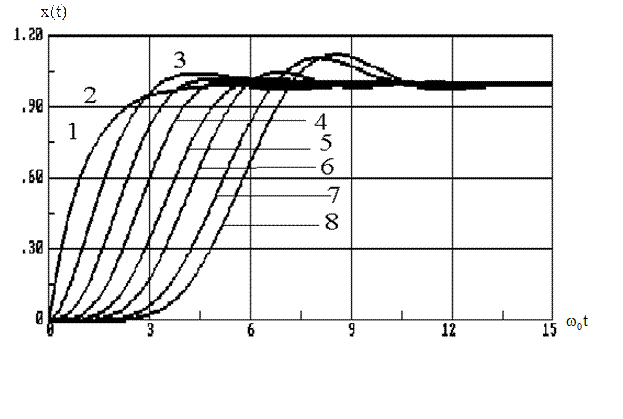 Рисунок 6 - Реакції систем,оптимізованих за критерієм
Рисунок 6 - Реакції систем,оптимізованих за критерієм  ,
, . (22)
. (22) .
.
 (23)
(23) , а
, а 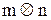 матрицю перетворення регулятора - через R. Тоді отримаємо
матрицю перетворення регулятора - через R. Тоді отримаємо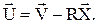 (24)
(24) . (25)
. (25) (26)
(26) буде матриця стовпець b. Прямокутна матриця R перетворюється в матрицю-рядок r. Така ж заміна відбудеться і в матричної передавальної функції замкнутої системи. Уявімо передавальну функцію об'єкта в наступному вигляді
буде матриця стовпець b. Прямокутна матриця R перетворюється в матрицю-рядок r. Така ж заміна відбудеться і в матричної передавальної функції замкнутої системи. Уявімо передавальну функцію об'єкта в наступному вигляді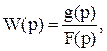 (27)
(27)
 (28)
(28) (29)
(29) (30)
(30) Після перетворень отримаємо систему рівнянь
Після перетворень отримаємо систему рівнянь (31)
(31)









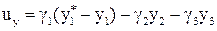 .
.
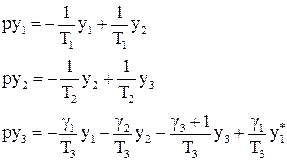




 і оберемо час керування
і оберемо час керування  . Згідно з рис. 3 для системи третього порядку перехідний процес закінчується в момент часу
. Згідно з рис. 3 для системи третього порядку перехідний процес закінчується в момент часу  . Тоді
. Тоді 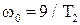 , а система алгебраїчних рівнянь для визначення коефіцієнтів зворотних зв’язків прийме вигляд
, а система алгебраїчних рівнянь для визначення коефіцієнтів зворотних зв’язків прийме вигляд
