 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Поняття про стійкість розв’язань диференційних рівнянь
Будь-яка система повинна бути перш за все працездатною. Це означає, що вона повинна нормально функціонувати при дії на неї різних зовнішніх збурень. Іншими словами, система повинна працювати стійко. Поняття стійкості системи керування пов'язане із здатністю повертатися в стан рівноваги після зникнення зовнішніх дій, які вивели її з цього стану. Дане визначення є фізичним поняттям стійкості. Наочно стійкість ілюструється наступним рисунком.
Ілюстрація поняття стійкості Тут положення кульки визначається координатою у. Виведемо кульку з положення рівноваги в точку y0 і відпустимо її. З аналізу зміни координати у(t) витікає: а) у(t)®0 при t®¥, стійке положення кульки; б) у(t)®¥ при t®¥, нестійке положення кульки; в) у(t)=y0=const при t³0, нейтральне або байдуже положення кульки. Таким чином, стійкість характеризується вільною поведінкою системи.
Стан системи можна зобразити точкою в просторі, координатами якого є змінні системи (x1, x2 ..., xn). Початок координат цього простору відповідає рівноважному стану системи. Тоді розв’язання рівняння динаміки системи можна розглядати як деяку траєкторію X(t) в просторі змінних (x1, x2, ... , xn).
Траєкторії руху, що відповідають стійкій і нестійкій системам
Щоб вирішити питання про стійкість системи, необхідно визначити траєкторію її руху в просторі станів, тобто знайти розв’язання диференціального рівняння, яке описує досліджувану систему. Лінійна система називається стійкою, якщо її вихідна координата залишається обмеженою при будь-яких обмежених по абсолютній величині вхідних діях. Стійка лінійна система повинна переходити від одного сталого стану до іншого при зміні задавальної дії. Стійкість лінійної системи визначається її характеристиками і не залежить від збурень, що діють на неї. Диференційне рівняння руху досліджуваної лінійної системи завжди можливо представити у вигляді
Розв’язання цього рівняння складається з суми двох розв’язань: частинного розв’язання неоднорідного рівняння з правою частиною і загального розв’язання однорідного рівняння без правої частини, тобто, рух системи складається з двох рухів – вимушеного, обумовленого правою частиною рівняння і вільного, обумовленого лівою частиною рівняння.
Система стійка, якщо при
Розв’язання цього рівняння має вигляд
де рі – корені характеристичного рівняння
сі - постійні інтегрування, що визначаються з початкових умов, які залежать від правої частини неоднорідного рівняння. Корені характеристичного рівняння залежать тільки від лівої частини рівняння. сі залежать як від лівої, так і від правої частини рівняння. Однак в поняття стійкості входить тільки факт наявності або відсутності загасання перехідного процесу і стійкість системи таким чином визначається тільки лівою частиною характеристичного рівняння. Для визначення стійкості необхідно розв’язати характеристичне рівняння і визначити корені. Корені характеристичного рівняння 1. Корінь дійсний негативний.
Розв’язання рівняння
Перехідний процес має вигляд
2. Корінь дійсний позитивний.
Розв’язання рівняння
Перехідний процес має вигляд
3. Корені комплексні з негативною дійсною частиною.
Розв’язання рівняння
Перехідний процес має вигляд
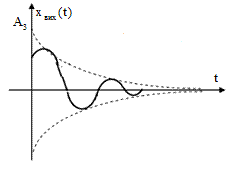
4. Корені комплексні з позитивною дійсною частиною.
Розв’язання рівняння
Перехідний процес має вигляд
5. Корені уявні.
Розв’язання рівняння
Перехідний процес має вигляд
Таким чином, для загасання вільного руху необхідно і достатньо, щоб дійсна частина усіх коренів була негативною, або ці корені на площині комплексного змінного були розташовані зліва від уявної вісі.
Комплексна площина коренів характеристичного рівняння Якщо корені характеристичного рівняння розташовані на уявній вісі, то система знаходиться на межі стійкості. При цьому можливі два випадки: корінь на початку координат і пара уявних коренів. Нульовий корінь з'являється, коли вільний член характеристичного рівняння рівний нулю. В цьому випадку межу стійкості називають аперіодичною. Якщо решту коренів цього рівняння мають негативні дійсні частини, то система стійка не щодо вихідного сигналу, а щодо його похідної, вихідний сигнал в сталому режимі має довільне значення. Такі системи називають нейтрально стійкими. У тому випадку, коли характеристичне рівняння має пару уявних коренів, межу стійкості називають коливальною. Якщо хоч би один з коренів лежить в правій напівплощині комплексної площини коренів характеристичного рівняння, то система нестійка. Обчислення коренів характеристичного рівняння високого порядку викликає певні труднощі. Тому для дослідження стійкості систем розроблені критерії (правила), що дозволяють судити про розташування коріння на комплексній площині без їх розрахунку. Перш ніж скористатися для оцінки стійкості тим або іншим критерієм, слід перевірити виконання необхідної умови стійкості. Необхідною, але недостатньою умовою стійкості системи є позитивність всіх коефіцієнтів характеристичного рівняння системи
тобто дотримання умови aі>0 для всіх i від 0 до n, де n - порядок системи.
3. Графічна інтерпретація математичного опису САК: Структурні схеми Систему автоматичного керування можна розглядати як комбінацію типових динамічних ланок. Зображення системи керування у вигляді сукупності типових і нетипових динамічних ланок з вказівкою зв'язків між ними носить назву структурної схеми системи. Ланка в цьому випадку виступає як елементарна структурна одиниця, перетворювач інформації. Структурні схеми складаються з окремих структурних елементів. Основними елементами структурних схем є наступні. 1. Ланка з одним входом і одним виходом: Y(p)=W(p)X(p).
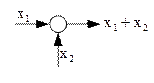
2. Ланка з двома входами і одним виходом (біля кожного входу записується своя передавальна функція):Y(p)=W1(p)X1(p)+W2(p)X2(p).
3. Лінія зв'язку і вузол (розгалуження), стрілка показує напрям передачі інформації.
4. Суматор.
5. Елемент порівняння.
В системах керування зустрічаються три види з'єднань ланок: послідовне, паралельне і з'єднання по схемі зі зворотнім зв’язком. Послідовне з'єднання ланок наведено на наступному рисунку, таке з'єднання характеризується тим, що вихід попередньої ланки подається на вхід наступної.
Послідовне з'єднання ланок
Вихідна величина послідовно з’єднаних ланок дорівнює
Звідки результуюча передавальна функція Wp(p) дорівнює
Отже, в загальному випадку можна записати
Таким чином, результуюча передавальна функція послідовно сполучених ланок рівна добутку передавальних функцій ланок. Паралельне з'єднанняланок зображене на наступному рисунку. Таке з'єднання характеризується тим, що на входи всіх ланок подається одна і та ж вхідна дія, а вихідна величина визначається сумою вихідних величин окремих ланок.
Паралельне з'єднання ланок
Вихідна величина паралельно з’єднаних ланок визначається y=y1+y2+y3, тобто
Тоді У загальному випадку
Таким чином, результуюча передавальна функція паралельно з’єднаних ланок дорівнює сумі передавальних функцій складових ланок. Зворотний зв'язок. Таке з'єднання ланок зображене на наступному рисунку. Воно характеризується тим, що вихідний сигнал ланки подається на його вхід.
З'єднання ланок за схемою із зворотним зв'язком
Зворотний зв'язок може бути позитивним (ПЗЗ), якщо сигнал y1, що знімається з виходу другої ланки, підсумовується з сигналом x на вході, і негативним (НЗЗ), якщо y1 віднімається. Крім того, зворотні зв'язки можуть бути жорсткими і гнучкими. Зв'язок називається гнучким, якщо передавальна функція W2(р) в сталому режимі дорівнює нулю. Для визначення результуючої передавальної функції такої комбінації ланок запишемо співвідношення:
де знак “+” відноситься до позитивного, а знак “-” - до негативного зворотного зв'язку. Звідки результуюча передавальна функція зворотного зв'язку має вигляд
У загальному випадку, складний ланцюг динамічних ланок, створюючих систему управління, включає комбінації всіх трьох розглянутих випадків, тобто є змішаним з'єднанням ланок. Користуючись виразами (4), (5) і (6), можна знайти загальну результуючу передавальну функцію змішаного з'єднання ланок. У тих випадках, коли структурна схема системи виявляється складною і містить перехресні зв'язки, її спрощують і зводять до простого еквівалентного вигляду, користуючись правилами перетворення структурних схем .
Поиск по сайту: |


 . (3)
. (3)
 вільний рух прагне до 0. Тобто необхідно дослідити однорідне рівняння
вільний рух прагне до 0. Тобто необхідно дослідити однорідне рівняння .
. ,
, .
. можуть бути дійсним
можуть бути дійсним 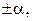 комплексними
комплексними 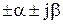 і чисто уявними
і чисто уявними  . Розглянемо поведінку системи з різними коренями характеристичного рівняння.
. Розглянемо поведінку системи з різними коренями характеристичного рівняння. .
.

 .
.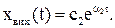

 .
.
 .
.

 .
.







 .
. .
. , (4) де n - число включених послідовно ланок.
, (4) де n - число включених послідовно ланок.
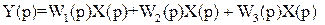 .
. .
. , (5) де n - число включених паралельно ланок.
, (5) де n - число включених паралельно ланок.
 ,
, , (6) де знак “+” відповідає НЗЗ, знак “-” - ПЗЗ.
, (6) де знак “+” відповідає НЗЗ, знак “-” - ПЗЗ.