 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Функционалы, вариации и их свойства
Динамические свойства синтезируемых оптимальных систем существенно зависят от вида оптимизирующего функционала, который является критерием качества управления. Общих правил выбора критериев качества для различных управляемых объектов не существует и назначение критерия оптимальности в каждом конкретном случае является самостоятельной задачей. Функционал качества должен выбираться таким образом, чтобы он, с одной стороны, наилучшим образом характеризовал цель управления, а с другой стороны, конкретная вариационная задача должна быть аналитически разрешимой. Задачей вариационного исчисления является отыскание функций, доставляющих экстремальное значение некоторым функционалам. Функционал можно рассматривать как функцию особого рода, в которой роль независимой переменной играет другая функция. В настоящее время в теории и практике оптимального управления широкое распространение получили интегральные функционалы
где
Для систем управления, динамика которых описывается дифференциальными уравнениями возмущенного движения (8.9), функционал (8.12) задает цель управления, которая характеризуется видом функции F. Остановимся подробнее на критериях оптимальности, наиболее приемлемых для систем управления электроприводами. Если в функционале (8.12) подынтегральное выражение F=l, то
Минимизация I1 соответствует наименьшему времени Т перехода системы (8.9) из начального положения η(0) в конечное η=0, при этом управление принадлежит некоторой замкнутой области, т.е. ограничено по модулю Оптимальное по быстродействию управление имеет смысл и может быть реализовано лишь в случае установившегося невозмущенного движения, когда начальная и конечная точки траектории зафиксированы. Такое управление применяется в электроприводах позиционных механизмов, осуществляющих перемещение рабочего органа из исходного положения в конечное. Для следящих электроприводов управление, оптимальное по быстродействию, лишено смысла в результате подвижности концов траекторий. Качество управления в этом режиме удобно задавать интегральными квадратичными функционалами. Если интегрант функционала (8.12)
Данный критерий характеризует площадь, ограниченную кривой квадрата отклонения координаты уi истинной траектории движения системы от координаты уi* заданной траектории. Наряду с критерием, где в качестве интегранта используют квадратичную ошибку, находят применение функционалы, характеризующие минимум абсолютного отклонения:
Функционалы (8.14) и (8.15) плохо учитывают колебательность переходного процесса, т.е. ничего определенного нельзя сказать о характере его протекания, является ли он колебательным или монотонным. С учетом недостатков критериев (8.14) и (8.15) был предложен обобщенный интегральный квадратичный критерий
В силу системы (8.9) функционал (8.16) может быть преобразован к виду
Интегралы (8.16) и (8.17) представляют собой взвешенную с помощью весовых коэффициентов wi (i=l,...,n) сумму площадей, ограниченных квадратами отклонений координат истинного движения от координат программного движения по каждой переменной состояния. Смысл этих критериев заключается в том, что они запрещают длительное существование не только отклонения основной регулируемой переменной ηi, но и ее производных. Поэтому минимизация функционалов (8.16) и (8.17) обеспечивает быстрое и плавное протекание переходных процессов. Интегральные критерии (8.14)-(8.17) не учитывают того, что в системе может иметь место ограничение мощности сигнала управления. Кроме того, система сама может иметь ограниченные энергетические ресурсы. Эти ограничения учитывают функционалы вида
Функционалы (8.14) и (8.15) при наличии ограничений (8.18) и (8.19) приводятся к одному из функционалов
Введение в функционал квадрата управляющего воздействия фактически приводит к обобщенной интегральной оценке и интеграл (8.20) может быть приведен к виду (8.16) или (8.17), что вполне естественно, т.к. ограничение управляющего воздействия соответствует ограничению всех координат управляемого объекта. Первое слагаемое подынтегральной квадратичной формы функционала (8.20) имеет тот же смысл, что и в функционале (8.17). Введение под интеграл слагаемого cU2, с одной стороны, означает достижение оптимальности гашения возмущенного движения при ограничении затрат энергии на управление, а с другой – обеспечивает поиск оптимального управления среди множества допустимых линейных функций. Таким образом, функционалы содержат в себе не только основные динамические свойства замкнутых систем, которыми те должны обладать, но и определяют класс функций, среди которых следует искать оптимальное управление. Минимизация квадратичных функционалов (8.14), (8.16)–(8.18), (8.20) осуществляется линейными управлениями, а для достижения экстремального значения функционалов вида (8.15), (8.19), (8.21), (8.22) с нелинейными интегрантами следует применять нелинейные законы управления. В некоторых литературных источниках указано, что функционал (8.14) минимизируется релейными управлениями, однако, такое утверждение представляется спорным. Многообразие приведенных функционалов еще раз показывает, что универсального критерия качества для различных систем не существует и синтезируемый закон управления является оптимальным в смысле минимизации вполне определенного функционала. Причем динамические свойства синтезируемой системы не всегда удовлетворяют желаемым, и процедуру синтеза по выбранному критерию целесообразно дополнять оценкой таких прямых показателей, как длительность переходного процесса, колебательность, максимальное перерегулирование, величина статической ошибки. Остановимся кратко на некоторых свойствах функций, функционалов и вариаций, без которых невозможно изложение последующего материала. Рассмотрим функцию f=x(t), каждому значению аргумента которой соответствует определенное значение х. Приращением аргумента функции называется разность Δt=t1–t2. Переменная величина Приращением, или вариацией δх аргумента x(t) функционала I называется разность между двумя функциями δх =xt(t) – x2(t). Функция x(t) непрерывна, если малому изменению t соответствует малое изменение x(t). Функционал непрерывен, если малому изменению x(t) соответствует малое изменение I. Если функционал содержит не только функцию, но и ее производные, понятие непрерывности функционала усложняется. В этом случае функционал непрерывен, если малому приращению функции и ее производных соответствует малое приращение функционала. Приращение функции x(t) определяется соотношением
Приращение функционала определяется аналогично
Линейная по отношению к Δt часть приращения функции называется дифференциалом функции и обозначается dx. Линейная по отношению к δх часть приращения функционала называется вариацией функционала и обозначается δI . Если дифференцируемая функция x(t) достигает экстремума в точке t0 области определения функции, то в этой точке dx=0. Если функционал I, имеющий вариацию, достигает экстремума внутри области определения на кривой x0(t), то в этом случае δI= 0. Функции, на которых достигается экстремум функционала, называются экстремалями. Вариационное исчисление можно рассматривать как обобщение дифференциального исчисления для многих переменных. Поэтому методы решения вариационных задач схожи с методами исследований функций на экстремум. Функционал I(x(t)) достигает минимума на x0(t), если его значение на любой близкой к x0(t) кривой x(t), не меньше, чем I(x0(t)) , т.е.
Аналогично определяются функции, на которых реализуется максимум. В этом случае Приведем понятие близости кривых. Кривые x0(t) и x(t) близки в смысле близости нулевого порядка, если модуль разности x0(t) – x(t) мал. Кривые x0(t) и x(t) близки в смысле близости первого порядка, если модули разностей x0(t) – x(t) и Если функционал I(x(t)) достигает на кривой x0(t) экстремума по отношению ко всем кривым, близким к x0(t) в смысле близости нулевого порядка, то такой экстремум называется сильным. Если функционал достигает экстремума лишь по отношению к кривым x(t), близким к x0(t) в смысле близости первого порядка, то такой экстремум называется слабым. Если достигается сильный экстремум, то достигается и слабый. В дальнейшем изложении предполагается слабый экстремум.
Поиск по сайту: |
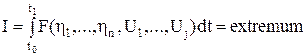 , (8.12)
, (8.12)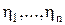 – компоненты вектора состояния объекта управления в прост-ранстве координат возмущенного движения;
– компоненты вектора состояния объекта управления в прост-ранстве координат возмущенного движения; – составляющие вектора управляющего воздействия.
– составляющие вектора управляющего воздействия.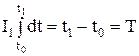 . (8.13)
. (8.13) .
. , то
, то . (8.14)
. (8.14) . (8.15)
. (8.15) . (8.16)
. (8.16) . (8.17)
. (8.17) . (8.18)
. (8.18)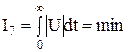 . (8.19)
. (8.19) . (8.20)
. (8.20) . (8.21)
. (8.21) . (8.22)
. (8.22) называется функционалом, зависящим от функции x(t), если каждой функции x(t) (из некоторого класса функций) соответствует определенное число I. Следовательно, каждому набору функций x1(t),...,xn(t), будут соответствовать числа I1,..., In.
называется функционалом, зависящим от функции x(t), если каждой функции x(t) (из некоторого класса функций) соответствует определенное число I. Следовательно, каждому набору функций x1(t),...,xn(t), будут соответствовать числа I1,..., In.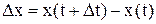 .
. .
. .
.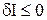 для всех кривых, близких к кривой x0(t).
для всех кривых, близких к кривой x0(t). малы. Кривые x0(t) и x(t) близки в смысле близости k-гo порядка, если
малы. Кривые x0(t) и x(t) близки в смысле близости k-гo порядка, если  (i=0,1,…,k), xi(t) – i-ая производная, ε – достаточно малое число.
(i=0,1,…,k), xi(t) – i-ая производная, ε – достаточно малое число.