|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Логическая сумма и логическое произведение событий⇐ ПредыдущаяСтр 19 из 19
Группы событий. Для анализа вероятности сложных событий полезно ввести понятие логической суммы (дизъюнкции) и логического произведения (конъюнкции) событий. Суммой событий А и В называют событие С = А U В , (П1.3) где U— знак логического суммирования (дизъюнкции). Событие С считается происшедшим, если произошло хотя бы одно из событий А и В или оба вместе. Произведением событий А и В является событие С = А ∩ В. (П1.4) Событие С считается свершившимся, если произошли каждое из событий Аи В. Иллюстрацией к понятию суммы и произведения событий может служить параллельное (рис. П1.1. а) и последовательное (рис. 54, б) соединение двух контактов.
а) б) Рис. П1.1. Замыкание цепи (событие С) при различном положении контактов (события А и В). Совокупность нескольких событий называется группой событий. Полная группа событий — совокупность событий, хотя бы одно из которых должно произойти. Например, событие А и противоположное событие Ẵ (отсутствие события А) составляют полную группу событий. Группа событий считается несовместной, если любые два события этой группы не могут произойти одновременно. Например, если признак (измеряемый параметр) разбит на три диагностических интервала, а события А1,А2, А3 означают появление признака в соответствующем интервале, то указанные события — несовместные. События А и Ẵ всегда образуют полную группу несовместных событий. Вероятность суммы событий. Разберем вопрос с помощью геометрической иллюстрации (рис. П1.2, а). Представим себе, что летящая частица с одинаковой вероятностью может попасть в любую точку прямоугольного поля, но не может миновать его (движение частицы в прямоугольной трубе).
а) б) в) Рис. П1.2. Схема мишеней для иллюстрации вероятности события А и вероятности суммы событий А и В.
Какова вероятность того, что частица попадает в мишень А (событие А)? Очевидно, эта вероятность
Р(А) = SA/S . (П1.5)
где SAиS — площади мишени и поля соответственно. Рассмотрим теперь вероятность суммы событий Р (А U В). Событие А U В осуществится, если частица попадет в мишень А, либо в мишень В, либо в обе мишени вместе. Иными словами, она должна оказаться в области, где имеется штриховка. Из простых соображений следует Р (А U В) = Р (А) + Р (В) - Р (А ∩В) , (П1.6)
где Р (А ∩ В)— вероятность совместного появления событий А и В (область пересечения кругов А и В, рис.П1.2 б). Если события А и В несовместные, то
Р(А U В)=Р(А)+Р(В) . (П1.7)
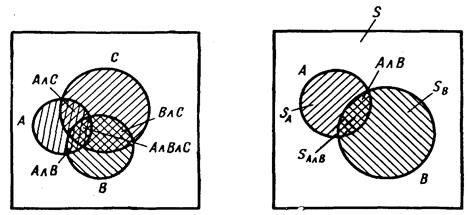
На рис. П1.2 несовместные события относятся к случаю, когда мишени А и В не пересекаются (случай в). Исходя из геометрических соображений (рис. П1.3), можно установить следующую формулу для трех событий:
Р(АUВUС) = Р (А)+Р(В) +Р (С) - Р(А∩В) - Р(В∩С) - Р(С∩А)+Р(А∩В∩С). (П1.8)
Рис.П1.3. Схема мишеней для суммы трех событий. Рис.П1.4. Схема мишеней для произведения событий.
Появление последнего слагаемого связано с тем, что в первых трех членах площадь А∩В∩С входит два лишних раза, но вычитается в каждом из трех следующих. Если события А, В и С несовместные (мишени не пересекаются), то Р (АUВUС) = Р(А) + Р(В) + Р(С) . (П1.9)
Отметим, что если события А, В и С образуют полную группу событий, т. е. хотя бы одно из них обязательно осуществится, то Р(AUBUC)=1. Для полной группы несовместных событий из условий (П1.8) и (П1.9) следует Р (А) + Р (В) + Р (С) = 1. В частности, для суммы вероятностей противоположных событий Р(A)+Р(Ẵ)=1. Вероятность совместного появления событий (вероятность произведения событий). В соответствии с геометрической иллюстрацией (рис.П1.4) вероятность совместного появления событий А и В (попадания частицы в мишени А и В одновременно)
Р (А∩В ) = S А∩ В /S , (П1.10) где S А∩В— площадь области перекрытия мишеней; S — общая площадь поля (вылетающая частица может с одинаковой вероятностью попасть в любую точку поля). Формула (П1.10) указывает прямой способ вычисления вероятности совместного появлений событий: число случаев, в которых проявились оба события, относится к общему числу возможных случаев. Очень важно найти связь вероятности сложного события с вероятностями составляющих его событий. Разделим и умножим правую часть равенства (П1.10) на величину S А — площадь мишени А. Тогда
Р (А∩В ) = (SA/ S)(S А∩ В /SА) . (П1.11)
Отношение SA/S = Р (А) представляет собой вероятность события А. Второе отношение обозначим
Р (В/А) = S А∩ В /SА . (П1.12)
В отличие от равенства (П1.10) площадь области А∩В, благоприятная для одновременного появления событий А и В, относится не ко всей площади S, а только к площади SA, где должно обязательно реализоваться событие А. Это означает, что прямоугольный канал, в котором лежит частица, заменяется каналом с сечением SAи событие А обязательно происходит, но событие В может происходить или не происходить. Вероятность события В при этом определяется отношением (П1.12). Величина Р (В/А) называется условной вероятностью события В (при условии, что событие А произошло). Из последних равенств получаем одну из наиболее часто применяемых формул теории вероятности Р (А ∩В) = Р (А) Р (В/А) . (П1.13)
Подобным образом (разделив и умножив правую часть равенства (П1.10) на SA) находим
Р (А∩В) = Р (В) Р (А/В) . (П1.14)
В теории вероятности более приняты сокращенные обозначения логического произведения событий в виде обычного алгебраического произведения, тогда равенства (П1.13) и (П1.14) запишут так:
Р (АВ) = Р (А) Р (В/А) = Р (В) Р (А/В). (П1.15)
Понятие условной вероятности приводит к весьма важному условию независимости событий. Событие В считается независящим от события А, если
Р (А/В) =Р(В) . (П1.16)
Рассмотрим геометрическую иллюстрацию условной вероятности по схеме мишеней. Если мишени А и В представляют собой два круга, то события А и В всегда являются зависимыми. Например, при расположении мишеней, показанных на рис.П1.5 а, условная вероятность Р (В/А) = 0,25. Если мишень В выходит из круга мишени А, то Р (В/А) =0, т. е. если известно, что частица попала в мишень А, то она не может одновременно пробить мишень В.
А) б) Рис. П1.5. Иллюстрация для зависимых и независимых событий. В каком случае попадания в мишени А и В будут независимыми событиями? Это будет в том случае, когда мишень В представляет собой совокупность равномерно распределенных кружков. На рис.П1.5 б части мишени В, попавшие в круг мишени А, отмечены черным цветом. Легко увидеть, что условие (П1.16) соблюдается. События А и В являются независимыми, совместными. Таким образом, несовместные события всегда зависимые, тогда как совместные события могут быть зависимыми или независимыми. Для независимых событий Р (АВ)=Р(А)Р(В) . (П1.17) Из соотношений (П1.14) и (П1.16) вытекает условие Р (А/В) = Р (А), т. е. независимость событий — понятие взаимное. Для группы из трех событий
Р(АВС)=Р(А)Р(В/А)Р(С/АВ)=Р(В)Р(А/В)Р(С/ВА)=Р(С)Р(А/С)Р(В/АС) (П1.18)
для независимых событий Р(АВС)=Р(А)Р(В)Р(С) . (П1.18)
Список литературы
1.Биргер И.А. “Техническая диагностика”. М: Машиностроение, 1998 - 240с. 2.Александров А.А. и др. “Вибрация и вибродиагностика судового электрооборудования”. - Л: Судостроение, 1996 - 276с. 3.Попков В.И., Мышинский Э.Л., Попков О.И. “Виброакустичекая диагностика в судостроении”. - Л.: Судостроение, 1989 - 256с. 4.Vibration Monitoring of Machines. Brüel & Kjær Technical review, 1996, № 11. 5. Proceedings of 30 the International Congress and Exhibition on Noise Control Engineering “Internoise - 2001”, Den Haag, Holland, 2001 August 27 -31. 6.Pulse system for vibration diagnostic of machines. Brüel & Kjær Technical review, 2001, № 1.
Поиск по сайту: |