 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Цифровые методы анализа вибросигналов
При вибродиагностике электромеханических систем обычно решаются задачи связанные с выделением сигналов с амплитудной и угловой модуляцией, суммы сигналов с совпадающими частотами от пространственно разнесенных источников и сигналов с большим числом кратных гармоник. Основным методом выделения модулирующих функций является метод основанный на преобразовании Гильберта описывающем комплексный сигнал x*(t) в виде
где x(t) - реальный сигнал;
Дискретное преобразование Гильберта (ДПГ) обычно строится на базе БПФ или ДПФ. Тогда некоторому аналоговому сигналу a(t) отвечает дискретный сигнал
где a(n) - дискретный ряд сигнала a(t) при 0 < n < N - 1; Тогда имеем комплексный спектр сигнала a(n) в виде [4] SA( r ) = F[W(n) * a(n)] , (3.32)
где F - матрица БПФ; W(n) - временная весовая функция (“окно”) выделяющая полосу анализа; 0 < r < N - 1 - шаг по частоте.
Спектральная плотность сигнала имеет вид
благодаря симметричности вещественных сигналов относительно точки N / 2. В вибродиагностике электромеханических систем важное место занимает анализ плотности спектральной мощности сигнала вибрации, имеющий вид
где Анализ сложных сигналов, представляющий собой сумму сигналов, от пространственно разнесенных источников вынуждающих сил осуществляется расчетом взаимных спектров сигналов sАВ измеряемых в разных точках бытовой машины
где sВ - спектральная плотность сигнала b(n). Рассчитав sАВ(r) можно получить взаимную корреляционную функцию Rab(n) [4]
где F-1 - матрица обратного БПФ; W( r ) - весовая функция в частной области. Взаимосвязь двух сигналов a(n) и b(n) легко установить по наличию у них общих спектральных составляющих в плотностях спектральной мощности. Это достигается расчетом функции когерентности
Функция когерентности измеряется изменяется от 0 до 1. Примеры характеристик сигналов a(t) и b(t) приведены на рис.3.12, 3.13. Выбор метода анализа вибросигналов при диагностике бытовых машин определяется сложностью объекта и значит вибрационных сигналов, характером конструкции, глубиной и целью диагностики.
а)
б)
в)
Рис. 3.12. Характеристики типовых синусоидальных сигналов разной частоты a(t) иb(t): a) - временные функции сигналов; б) - плотности спектральных мощностей сигналов
а)
б)
Рис. 3.13. Характеристики типовых синусоидальных сигналов разной частоты a(t) иb(t): a) - функция когерентности двух сигналов
Поиск по сайту: |
; (3.30)
- преобразование Гильберта от исходного сигнала x(t) в текущий момент времени t’.
; (3.31)
(n) - преобразование Гильберта от a(n).
(3.33)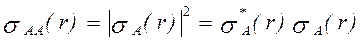
, (3.34)
- комплексносопряженная по Гильберту спектральная плотность.
, (3.35)
; (3.36)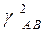
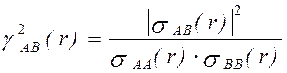; (3.37)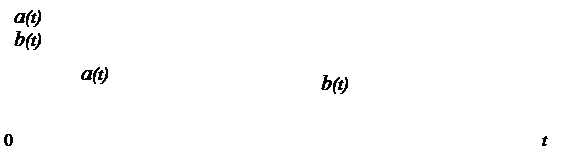
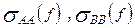; в) - плотность взаимной спектральной мощности сигналов 
.
;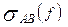