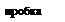Главная | Обратная связь

Археология Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика

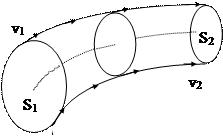
Уравнение неразрывности ⇐ ПредыдущаяСтр 10 из 10   Как уже отмечалось, при стационарном движении жидкости (или газа) скорость ее частиц не изменяется с течением времени. Для наглядности вводится понятие линии тока, которые представляют собой линии, касательные к которым в любой точке совпадают по направлению с вектором скорости в этой же точке. В случае стационарного движения линии тока неподвижны и совпадают с траекториями частиц жидкости. Кроме того, для облегчения изучения движения жидкости вводится понятие трубки тока. Эти трубки образуются так, что линия тока, проходящая через какую-либо точку, лежащую на поверхности трубки тока, целиком лежит на этой поверхности (см. рис.40). При стационарном течении жидкости       S     Рис.40. Трубка тока. стенки трубки тока неподвижны. Жидкость, вошедшая в трубку, в дальнейшем движется все время внутри ее. Поэтому выделенную трубку можно рассматривать независимо от остальной жидкости. Предположим, что выделенная трубка тока настолько тонка, что в каждой точке ее поперечного сечения величину скорости частиц жидкости можно бы- ло бы считать одинаковой. Пусть в сечении S1(рис.40) скорость частиц жидкости равна v1. За промежуток времени Dt через сечение пройдет объем жидкости V1= = v1Dt S1. Если плотность жидкости в этом сечении равна r1, то через сечение проходит масса m1 = r1V1 = r1v1Dt S1. Аналогично через сечение S2 за время Dt проходит масса m2 = r2v2Dt S2 . При стационарном движении количество вещества, проходящее через сечения S1 и S2 , должно быть одинаковым, т.е. m1= m2. Поэтому r1v1Dt S1 = r2v2Dt S2. При несжимаемости жидкости r1= r2 , откуда следует, что v1 S1 = v2 S2 , или в общем виде v S = const . ( 10-7 ) Выражение ( 10-7 ) носит название уравнения неразрывности. Примером проявления свойств жидкости, описываемых этим уравнением, может служить течение рек: в узких местах скорость течения возрастает и, наоборот, в широких местах скорость течения становится меньше. § 10-3. Уравнение Бернулли и его следствия. h2 h1 S2 S2 S1 S1 Рис.41. Выделенный эле- Мент трубки тока.

Выделим в трубке тока (см.рис.41) элемент, ограниченый плоскими сечениями S1 и S2. Пусть скорости движения жидкости в этих сечениях равны v1 и v2 , а давления р1 и р2 соответственно. За время Dt выделенный элемент перемещается в направлении, указанном стрелкой, так, что сечения S1 и S2 cмещаются на расстояния Dl1 = v1Dt и Dl2 = v2 Dt соответственно, занимая новые положения S1 и S2 (см. рис.). При перемещении изменяется кинетическая и потенциальная энергии выделенного элемента. По закону сохранения энергии величина этого изменения определяется работой сил давления f1 = p1S1 и f2 = p2S2,

которые действуют на плоскости S₁ и S₂. Как видно из рис., часть элемента между сечениями S₁ и S₂ остается неподвижной так, что изменение положения выделенного элемента сводится к перемещению отрезка, ограниченного сечениями S₁ и S₁ в новое положение между плоскостями S₂ и S₂. Пусть плотность жидкости в сечении S₁ равна r₁, а в сечении S₂ - r₂. Масса отрезка между сечениями S₁ и S₁ равна m₁ = r₁v₁S₁Dt, тогда как масса между S₂ и S₂ равна m₂ = r₂v₂S₂Dt; поэтому кинетическая и потенциальная энергии массы m₁ равны:

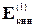= . ( 10-8 )

Аналогично для массы m₂:

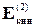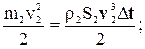
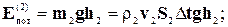= ( 10-9 )

где h₁ и h₂ - высоты центров тяжести первого и второго элементов относительно выбранного уровня отсчета потенциальной энергии.

На основании закона сохранения механической энергии можно записать:

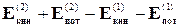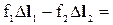
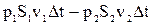= . ( 10-10 )

Работа силы f₂ взята со знаком минус потому, что направление силы и направление перемещения противоположны друг другу.

Подставляя в уравнение (10-10) значения кинетических и потенциальных энергий (10-8) и (10-9), получаем:

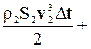
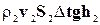
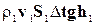= , ( 10-11 )

откуда после сокращения на величину Dt (с учетом того, что v₁S₁ =v₂ S₂) следует:

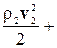
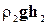
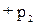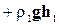
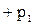= ,( 10-12 )

или в общем виде:

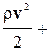
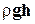+ р = const. ( 10-13 )

Выражения (10-12) и (10-13) представляют различные формы записи уравнения Бернулли, имеющего ряд важных следствий практического характера.Если дви-жение жидкости или газа происходит на постоянной высоте, то уравнение (10-13) упрощается: 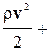р = const, или 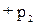= 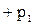.( 10-14 )

Из этого уравнения следует, что давление внутри трубки тока зависит от скорости: там, где скорость меньше, давление больше, при увеличении скорости потока

давление в нем уменьшается. Это утверждение называют принципом Бернулли.

Возникновение подъемной силы крыла.

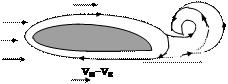
vп vп+vв   Рис.42. Обтекание крыла воздушным потоком.

Профиль крыла изображен на рис.42. Воздушный поток, обтекая крыло, образует в области позади его вихрь, направление вращения которого показано на рис. По закону сохранения момента импульса вокруг крыла должен образоваться круговой поток с обратным направлением вращения16 (см.рис.42). Ес-ли обозначить скорость частиц в вихре вокруг крыла vв, то, как видно из рис., на верхней части крыла

скорость вихря складывается со скоростью v_п воздушного потока, тогда как под крылом скорость вихря направлена против скорости потока, и они вычитаются. Таким образом получается, что общая скорость воздуха над крылом больше, чем под крылом, и из принципа Бернулли следует, что давление в потоке воздуха под крылом больше, чем в потоке над крылом, т.е. возникает результирующая сила, направленная вверх и известная как подъемная сила.

Нечто похожее наблюдается при обтекании неподвижной крыши потоками воздуха при ураганных ветрах: внутри дома воздух неподвижен, тогда как на наружной части крыши его скорость достигает 40 М/c. В этом случае давление воздуха изнутри, которое больше наружного, как бы поднимает крышу вверх. При больших скоростях потока прочности конструкции скрепляющих балок может оказаться недостаточно; в этом случае ветер снесет крышу с дома.

 

Рис.43. Пульверизатор.

Еще одним примером проявления принципа Бернулли служит пульверизатор, который схематически изображен на рис.43. Если пробка сосуда, содержащего жидкость, плотно прижата, то при сжимании резиновой груши образуется ток воздуха, давление в потоке уменьшается, и под давлением воздуха, находящегося внутри сосуда, жидкость устремляется вверх. Оконечность горизонтальной трубки сужена в виде сопла, что способствует еще большему увеличению скорости потока воздуха, который увлекает за собой капли поднимающейся жидкости.

Аналогом пульверизатора является пульт для разбрызгивания краски или побелки. В домашних условиях обычно используется упрощенный вариант этого устройства, где поток воздуха создается обыкновенным пылесосом. Для этого достаточно всасывающий шланг присоединить к выходному отверстию пылесоса.

 

9 Теория базируется на постулате постоянства скорости света как максимально возможной скорости передачи информации и преобразованиях Лоренца. В нашем курсе она изучаться не будет.

10 Существует правило, определяющее направление силы Кориолиса, которое гласит, что в северном полушарии силы инерции стремятся отклонить тело вправо, если смотреть по ходу движения, а в южном - влево. Следует по-мнить, однако, что это правило получено в некотором приближении. Более точное решение задачи на вычисление полного выражения силы Кориолиса показывает наличие вертикальной составляющей такой силы.

11 Непериодическая физическая величина может быть представлена в виде интеграла Фурье, содержащего бесконечно много спектральных составляющих.

12 Напомним, что потенциальная энергия определяется неоднозначно, и начало отсчета этой энергии может быть выбрано произвольно.

13 x=Asin(w₀t+j); dx = Aw₀cos( w₀t+ j)dt

14 Силы трения иногда называют диссипативными силами, поскольку работа против них в конечном счете превращается в тепло, т.е. рассеивается в пространство.

15 Предполагается, что силы вызывают деформации, которые не выходят за пределы упругости.

16 В реальных жидкостях существование такого потока доказывает эффект Магнуса: если поместить в движущуюся жидкость горизонтально расположенный цилиндр, способный свободно вращаться вокруг своей продольной оси, то цилиндр начинает вращаться так, что направление движения его верхних точек совпадает с направлением потока жидкости.

⇐ Предыдущая12345678910

 

Поиск по сайту: