 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Потенциальная энергия
Пусть имеются две материальные точки С и D (см. рис.23.), взаимодействие
Наконец, та же самая конфигурация может быть получена при обоюдном перемещении точек С и D. В этом случае работу совершают обе силы FCD и FDC , ноихобщаяработа останется той же самой, если сумма перемещений точек по-прежнему равна DD* или CC*. Полученный вывод можно распространить и на систему материальных точек: суммарная работа всех потенциальных сил взаимодействия зависит лишь от начальной и конечной конфигурации системы. Знак работы при этом может, вообще говоря, любым - работа может как положительной так и отрицательной. Когда работа отрицательна, т.е. угол между силой и перемещением равен 1800, то ее можно совершить лишь за счет внешнего воздействия, и, наоборот, работа положительная ( направление перемещения совпадает с направлением силы ) может совершаться системой без какого-либо внешнего воздействия. Например, для сжатия пружины нужно приложить некоторое усилие, а сжатая пружина, распрямляясь, сама способна совершить работу. В этом случае говорят, что положительная работа совершается за счет «запаса» этой работы в самой системе. Если в системе материальных точек действует несколько различных по своей природе потенциальных сил, которые в этом случае называются внутренними, то общий «запас» положительной работы складывается из « запасов» каждого из видов взаимодействия. Поскольку выбор начальной конфигурации весьма условен, то можно утверждать, что практически любой конфигурации DU = U2 - U1 = - A12 , ( 6-11 ) т.е. изменение потенциальной энергии при некотором изменении конфигурации определяется суммарной работой всех внутренних потенциальных сил , взятой с обратным знаком. Точка начала отсчета потенциальной энергии может быть выбрана произвольно, т.к. для решения практических задач важным оказывается не сама величина потенциальной энергии, а лишь ее изменения. Например, можно считать, что камень, лежащий на поверхности Земли, имеет нулевую потенциальную энергию, хотя если ему предоставить возможность падать к центру Земли, то
§ 6-3. Кинетическая энергия.
Если на тело массы m действует некоторая сила F, сообщая ему ускорение а, то эта сила совершает определенную работу, которая связана с изменением скорости тела. Величина элементарной работы определяется так же, как и ранее: dA = F cosadl = ma cosa d l, где направление силы совпадает с направлением ускорения. Тогда acosa =
Пусть dt - промежуток времени, за который тело проходит отрезок dl . Тогда
т.к. dA = m d ( где величина Т =
т.е. изменение кинетической энергии тела за некоторый промежуток времени равно суммарной работе, совершенной всеми силами, действующими на тело в этот же промежуток времени. § 6-4. Закон изменения и сохранения механической энергии.
Полная механическая энергия системы материальных точек Е складывается из его кинетической энергии Т и потенциальной энергии U, т.е. Е = Т + U. ( 6-16 ) При движении точек внутри системы изменяются как скорости точек, так и их взаимное расположение. Пусть скорость произвольной точки ( i - точки ) изменяется под действием сил со стороны других точек. Полное изменение кинетической энергии i - точки в соответствии с выражением ( 6-15 ) определяется работой всех сил, действующих на эту точку - как внутренних так и внешних: D T i = A i . ( 6-17 ) Cложив выражения ( 6-17 ) для всех точек системы, получим:
Левая часть этого уравнения является кинетической энергией всей системы, которую можно обозначить D Т, а правая часть есть общая работа всех сил, которую 1. работы всех внутренних потенциальных сил - А внутр. пот ; 2. работы всех внутренних непотенциальных сил - А внутр. непот ; 3. работы всех внешних сил - А внеш . При этом надо учесть, что суммарная работа всех внутренних потенциальных сил с обратным знаком равна изменению потенциальной энергии системы D U. Поэтому равенство ( 6-18 ) приобретает такой вид: DТ = - DU + А внутр. непотен + А внеш . Перенося DU в левую часть этого равенства и замечая, что D Т + DU = DЕ, получим: D Е = А внутр. непотен + А внеш . ( 6-19 ) Выражение ( 6-19 ) представляет собой закон изменения механической энергии: изменение полной механической энергии системы материальных точек за некоторый промежуток времени равно суммарной работе всех внутренних непотенциальных и всех внешних сил за этот промежуток времени. Если система замкнута, т.е. на нее не действуют никакие внешние силы или сумма всех внешних сил равна нулю, а все внутренние силы являются потенциальными, то D Е = 0, и выражение Е = Т + U = const ( 6-20 ) представляет собой закон сохранения полной механической энергии . В качестве примера применения этого закона рассмотрим вывод так называемой второй космической скорости, под которой подразумевается скорость, которую необходимо сообщить телу, чтобы оно оказалось способным преодолеть притяжение Земли. Для этого используем выражение ( 6-7 ) для работы силы тяжести при удалении тела на бесконечно большое расстояние от Земли:
( g - ускорение свободного падения на поверхности Земли ), откуда следует, что вторая космическая скорость VII равна:
Поиск по сайту: |

 C C * D* D
· · · ·
FDC FCD
Рис.23. Изменение кон-
фигурации рас по-
ложения точек.
C C * D* D
· · · ·
FDC FCD
Рис.23. Изменение кон-
фигурации рас по-
ложения точек.



 конфигурации расположения точек: та же самая конфигурация может быть достигнута, если точка С вообще остается на месте, а точка D перемещается в новое
конфигурации расположения точек: та же самая конфигурация может быть достигнута, если точка С вообще остается на месте, а точка D перемещается в новое 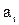 яв-
яв- . С учетом этого выражение для dA равно:
. С учетом этого выражение для dA равно: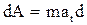 l =
l = 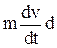 l. ( 6-12 )
l. ( 6-12 ) , ( 6-13 )
, ( 6-13 )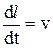 - скорость тела за промежуток времени dt. Принимая во внимание, что в механике Ньютона масса не зависит от скорости, выражение ( 6-13 ) можно
- скорость тела за промежуток времени dt. Принимая во внимание, что в механике Ньютона масса не зависит от скорости, выражение ( 6-13 ) можно ) = d (
) = d ( 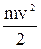 ) = d T, ( 6-14 )
) = d T, ( 6-14 ) = Т2 - Т1 = D Т, ( 6-15 )
= Т2 - Т1 = D Т, ( 6-15 )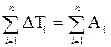 . ( 6-18 )
. ( 6-18 )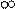 А = -
А = - 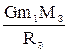 .
.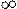 Т.к. гравитационные силы потенциальны, величина этой работы, взятая с обратным знаком, определяет значение потенциальной энергии притяжения тела к Земле - А = - U . Тогда из закона сохранения энергии следует что, тело может преодолеть притяжение Земли, если ему сообщить кинетическую энергию TII , которая равна потенциальной энергии притяжения:
Т.к. гравитационные силы потенциальны, величина этой работы, взятая с обратным знаком, определяет значение потенциальной энергии притяжения тела к Земле - А = - U . Тогда из закона сохранения энергии следует что, тело может преодолеть притяжение Земли, если ему сообщить кинетическую энергию TII , которая равна потенциальной энергии притяжения: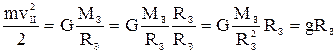 ,
,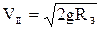 »11,2 кМ/С . ( 6-21 )
»11,2 кМ/С . ( 6-21 )