 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Колебания математического и физического маятников
Из школьного курса физики известно, что математический маятник представляет собой точечную массу, подвешенную на длинной невесомой и нерастяжимой нити. На первый взгляд раскачивание такой системы связано с изменением по меньшей мере двух координат сразу так, что для описания такого движения на- I где I - момент инерции точечной массы относительно точки подвеса, М - момент всех внешних сил,
Момент инерции точечной массы m, находящейся на расстоянии l от оси вращения, по определению равен I = m l2 , а единственной силой, момент которой относительно оси вращения отличен от нуля, является сила тяжести. Ее момент относительно оси, проходящей через точку подвеса, равен M = mgh = mg lsin j, и уравнение динамики вращательного движения принимает вид:
или после сокращения обеих частей на величину ml :
Знак минус в уравнениях ( 8-21) и ( 8-22 ) появился потому, что направление отсчета угла j взято против часовой стрелки, тогда как момент силы тяжести стремится повернуть маятник по часовой стрелке. Для малых углов отклонения j синус угла можно разложить в ряд Тэйлора по малому параметру j: f (x) = f (0) + Поскольку sin 0 = 0, то в разложении синуса исчезнут члены, содержащие f(0) и вторую производную sin j = j - Даже для углов отклонения около 300, т.е. 0,5 рад ( в математике угол обычно измеряется в радианах; один радиан » 570 ), вторая поправка в разложении синуса дает величину, чуть большую двух процентов, поэтому с достаточной степенью точности функцию синуса можно заменить его аргументом так, что уравнение ( 8-22 ) приобретает такой вид:
что полностью совпадает с уравнением движения груза на пружине. Поэтому нетрудно придти к заключению, что частота колебаний математического маятника определится также, как частота собственных колебаний груза на пружине:
производиться не будет. Частота собственных колебаний физического маятника равна: W =
Поиск по сайту: |
 , ( 8-20)
, ( 8-20)
 - угловое ускорение массы, которое, в свою очередь, определяется как вторая производная по времени от угла j отклонения от вертикали (см. рис. 33).
Рис.33. Колебания математического маятника.
- угловое ускорение массы, которое, в свою очередь, определяется как вторая производная по времени от угла j отклонения от вертикали (см. рис. 33).
Рис.33. Колебания математического маятника.
 , ( 8-21)
, ( 8-21) . ( 8-22 )
. ( 8-22 )
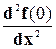 и синус угла j равен:
и синус угла j равен:
 , ( 8-23 )
, ( 8-23 )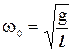 . ( 8-24)
. ( 8-24)







 О
l цм
j
mg
Рис.34. Физический
маятник.
О
l цм
j
mg
Рис.34. Физический
маятник.
 , ( 8-25)
где lцм обозначает расстояние, на котором расположен центр масс тела от оси вращения (см.рис.34). Однако те-
теперь момент инерции такого маятника требует специального вычисления, которого в рамках нашего курса
, ( 8-25)
где lцм обозначает расстояние, на котором расположен центр масс тела от оси вращения (см.рис.34). Однако те-
теперь момент инерции такого маятника требует специального вычисления, которого в рамках нашего курса
 . ( 8-26)
. ( 8-26)