 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лекция 8. Дифференциальное уравнение колебаний
Свободные колебания. Рассмотрим колебания груза массы m, висящего на пружине, жесткость которой k. Направим ось координат Х вертикально вниз, причем за начало отсчета
частотой.Пусть в некоторый момент времени смещение груза равно х. Тогда второй закон Ньютона в проекции на ось Х может быть записан в следующем виде: max = mg - k (x +x) или с учетом ( 8-1) max = - kx . ( 8-2 ) В свою очередь, уравнение ( 8-2 ) можно записать иначе, если представить ускорение тела через вторую производную смещения по времени ax = d2x/dt 2 и обозначить величину k/m =
Уравнение ( 8-3 ) является дифференциальным уравнением второго порядка, однако его решение можно просто угадать простым перебором всех элементарных функций, из которых только функции синуса и косинуса удовлетворяют решению этого уравнения. Действительно, если смещение x = A sin(w0t + j), ( 8-4 )
то скорость тела и ускорение тела Сравнение ( 8-4 ) и ( 8-6 ) показывает, что действительно ( 8-4 ) является решением уравнения ( 8-3 ). Величины А и j остаются произвольными, для их определения необходимо использовать начальные условия, т.е. значения смещения и скорости тела в начальный момент времени. Например, если при t = 0 x (0)= 0, а v(0) = v0, то из ( 8-4 ) следует, что sinj = 0 и j = 0, a из ( 8-5 ) величина А = v0/w0 . При этих условиях решением уравнения ( 8-3) служит функция х(t) = Задание тех или иных начальных условий обычно определяется конкретными условиями поставленной задачи.
Затухающие колебания.
В реальной жизни любой колебательный процесс постепенно затухает из-за наличия сил трения. Для колебаний груза на пружине существенную роль играет так называемое вязкое трение, сила которого при малых смещениях оказывается пропорциональной величине скорости тела: Fтрен = - bv = - b В этом случае второй закон Ньютона ( уравнение движения ) для груза, колеблющегося на пружине, приобретает такой вид:
Вводя обозначения
где по-прежнему
С учетом этого уравнение ( 8-9 ) может быть записано в таком виде:
После сокращения на величину
Сравнивая полученное уравнение с выражением (8-3), нетрудно заметить их почти полную идентичность; различие состоит лишь в том, что частота колебаний в
где как и ранее величины А и j определяются из начальных условий. В большинстве случаев b<<w0 и w3 » w0 . Решение ( 8-11) представляет уже негармоническое колебание, т.к. его амплитуда А
т.е. декремент затухания равен относительному уменьшению амплитуды за время, равное периоду колебания. Натуральный логарифм D называют логарифмическим декрементом затухания d, т.е. d = ln D =bТ .
Поиск по сайту: |
























 X
k kx x
m О
X
k kx x
m О
 mg х
Рис.32. Колебания
груза на
пружине.
mg х
Рис.32. Колебания
груза на
пружине.
 :
: = -
= -  , ( 8-5 )
, ( 8-5 )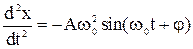 . ( 8-6 )
. ( 8-6 ) .
. . ( 8-7 )
. ( 8-7 )
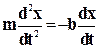 + mg - k (x +x). ( 8-8 )
+ mg - k (x +x). ( 8-8 ) , это уравнение можно преобразовать так:
, это уравнение можно преобразовать так: , ( 8-9 )
, ( 8-9 ) . Решение этого дифференциального уравнения может быть получено обычным способом, но можно показать, что уравнение ( 8-9 ) можно свести к уравнению типа ( 8-3 ). Для этого достаточно ввести замену переменных x(t) = z (t)e - bt. Проводя операцию дифференцирования, имеем:
. Решение этого дифференциального уравнения может быть получено обычным способом, но можно показать, что уравнение ( 8-9 ) можно свести к уравнению типа ( 8-3 ). Для этого достаточно ввести замену переменных x(t) = z (t)e - bt. Проводя операцию дифференцирования, имеем: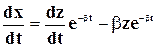 ; 2b
; 2b  ;
; ,
,  .
. +
+ 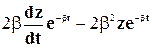 +
+  = 0
= 0 и приведения подобных членов получаем:
и приведения подобных членов получаем: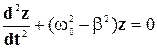 . ( 8-10)
. ( 8-10) . Таким образом решение уравнения
. Таким образом решение уравнения , ( 8-11)
, ( 8-11) , ( 8-12 )
, ( 8-12 )