 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приборы и принадлежности
Вискозиметр, исследуемые жидкости, секундомер. Описание вискозиметра.
Порядок выполнения работы Вискозиметр промывают испытуемой жидкостью. Укрепляют его в штативе и наливают испытуемую жидкость в колено 9 до метки 8. Осторожно с помощью резиновой груши всасывают жидкость выше метки 7 в резервуар 5. Определяют время истечения жидкости Таблица 1
Определение коэффициента внутреннего трения глицерина по методу Стокса. Обоснование метода
Обозначим скорость шарика относительно жидкости через L=k×r. (16) Величина коэффициента пропорциональности несколько различна для передней и задней частей тела, поэтому под градиентом скорости следует понимать среднее значение градиента скорости на поверхности шара
Полная сила трения, испытываемая движущимся шариком
где Согласно Стоксу, величина
т. е. сила трения прямо пропорциональна вязкости жидкости, радиусу шара и скорости его движения. Выражение (19) носит название закона Стокса:
В случае падения шарика в жидкости, все три силы будут направлены по вертикали. Если шарик движется равномерно, то такое движение шарика называется установившимся. Физически это означает, что сила трения и сила Архимеда уравновешиваются силой тяжести, т. е. движение происходит по инерции с постоянной скоростью. Тогда уравнение (18) можно переписать:
Последнее выражение позволяет определить коэффициент внутреннего трения в жидкости, в которой движется шарик. Так как жидкость всегда находится в каком-то сосуде, имеющем стенки, то учет наличия стенок несколько изменит выражение для коэффициента вязкости. Для жидкости, находящейся в цилиндре с радиусом
Поиск по сайту: |
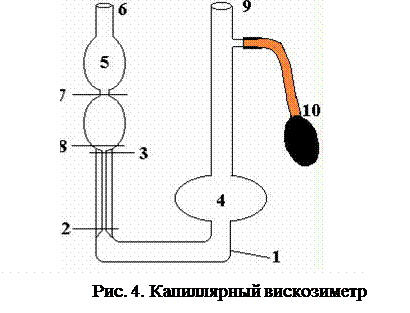 Капиллярный вискозиметр (рис. 4) представляет собой U- образную трубку, укрепленную вертикально. Участок трубы 2-3 выполнен в виде узкого канала; правое колено содержит шарообразное расширение 4; левое колено содержит двойное расширение 5, переходящее в верхней части в трубку 6. Метки 7-8 около верхнего расширения ограничивают определенный объем жидкости. Жидкость наливается в колено до заполнения почти всего шарообразного расширения 4. На трубку надета груша 10, при помощи которой жидкость засасывается в резервуар 5 выше метки 7.
Капиллярный вискозиметр (рис. 4) представляет собой U- образную трубку, укрепленную вертикально. Участок трубы 2-3 выполнен в виде узкого канала; правое колено содержит шарообразное расширение 4; левое колено содержит двойное расширение 5, переходящее в верхней части в трубку 6. Метки 7-8 около верхнего расширения ограничивают определенный объем жидкости. Жидкость наливается в колено до заполнения почти всего шарообразного расширения 4. На трубку надета груша 10, при помощи которой жидкость засасывается в резервуар 5 выше метки 7. (в момент, когда мениск проходит через метку 7, включают секундомер, а при прохождении мениска через метку 8 секундомер выключают). Время истечения жидкости измеряется 5 раз. Аналогичные опыты проделывают с водой. Время истечения воды
(в момент, когда мениск проходит через метку 7, включают секундомер, а при прохождении мениска через метку 8 секундомер выключают). Время истечения жидкости измеряется 5 раз. Аналогичные опыты проделывают с водой. Время истечения воды  . Значения
. Значения  берутся из справочников. Результаты расчетов по формуле (15) и экспериментальные измерения заносят в таблицу 1
берутся из справочников. Результаты расчетов по формуле (15) и экспериментальные измерения заносят в таблицу 1
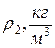
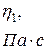
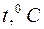
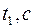
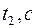
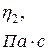
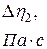
 На твердый шарик, падающий в жидкости, действуют три силы: сила тяжести, сила Архимеда и сила трения шарика о жидкость. Эти силы равны соответственно
На твердый шарик, падающий в жидкости, действуют три силы: сила тяжести, сила Архимеда и сила трения шарика о жидкость. Эти силы равны соответственно 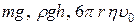 .
. . Молекулы жидкости в слое, прилегающем к шарику, движутся со скоростью
. Молекулы жидкости в слое, прилегающем к шарику, движутся со скоростью 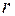 :
: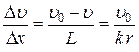 . (17)
. (17)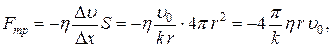 (18)
(18)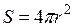 .
. для шара равна
для шара равна 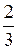 . Следовательно,
. Следовательно,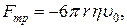 (19)
(19)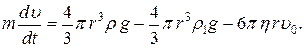 (20)
(20) . (21)
. (21) , коэффициент вязкости равен:
, коэффициент вязкости равен: (22)
(22)