 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Потенциал межмолекулярного взаимодействия
Взаимодействие молекул удобно характеризовать зависимостями силы f(r) и потенциальной энергией взаимодействия U(r), как функциями расстояния r между центрами сблизившихся молекул, приведенными на рис. 1 и 2. При построении этих кривых сила взаимодействия и потенциальная энергия молекул, находящихся на бесконечно большом расстоянии друг от друга, положены равными нулю. На расстояниях r>r0 (рис. 1) между молекулами действуют силы взаимного притяжения (отрицательный знак силы), а при r<r0 силы отталкивания (положительный знак силы). Из рис. 1 видно, что по абсолютному значению сила притяжения растет с увеличением r вплоть до некоторого значения r1. Затем сила уменьшается и при расстоянии r0 между атомами становится равной нулю. При дальнейшем уменьшении r сила вновь появляется, но уже сила отталкивания, быстро растущая с уменьшением расстояния между молекулами, стремясь к бесконечности при Кривой f(r) соответствует похожая на нее кривая U(r) (рис. 2). Сходство кривых не должно удивлять, так как f и U связаны, как известно, соотношением При расстоянии между атомами r0, когда сила взаимодействия равна нулю, потенциальная энергия проходит через минимум. О молекуле в таком положении принято говорить, что он находится на дне “потенциальной ямы”. Это положение равновесия, т. е. силы притяжения уравновешиваются силами отталкивания. Какой–либо универсальной формулы U(r), пригодной для всех молекул, не существует. Более точно характеристика U(r) может быть дана лишь конкретно для данных молекул. Во многих вопросах теории к хорошим результатам приводит следующая аппроксимация функции U(r):
в которой постоянные В теории уравнения состояния Ван–дер–Ваальса применяется более грубая аппроксимация. Крутой участок кривой U(r) заменяется вертикальной прямой, как это изображено на рис. 2 пунктиром. Если d – расстояние этой прямой от начала координат, то центры взаимодействующих частиц не могут сблизиться на расстояние, меньше d. Расстояние d играет роль диаметра молекулы, который относится к числу не вполне четко определяемых величин. Рассматриваемая аппроксимация соответствует модели твердых упругих шаров, между которыми действуют силы притяжения; силы отталкивания учитываются тем, что размеры шаров считаются конечными.
Поиск по сайту: |
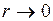 .
. .
. , (1)
, (1)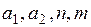 подбираются из требований наилучшей аппроксимации реального потенциала. Как показало исследование потенциалов, в большинстве случаев хорошим приближением являются n=12, m=6 при
подбираются из требований наилучшей аппроксимации реального потенциала. Как показало исследование потенциалов, в большинстве случаев хорошим приближением являются n=12, m=6 при  , уточняемых для конкретных атомов. Функция U(r), описываемая уравнением (1), называется потенциалом Леннарда–Джонса, широко используется в теории жидкостей и газов. Первый член (1) соответствует силам отталкивания, второй – силам притяжения, которые называются силами Ван–дер–Ваальса.
, уточняемых для конкретных атомов. Функция U(r), описываемая уравнением (1), называется потенциалом Леннарда–Джонса, широко используется в теории жидкостей и газов. Первый член (1) соответствует силам отталкивания, второй – силам притяжения, которые называются силами Ван–дер–Ваальса.