 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Порядок выполнения работы. Закрыть кран и накачать воздух в баллон (процесс1-2) так
Закрыть кран и накачать воздух в баллон (процесс1-2) так, чтобы величина Обработка результатов Используя полученные данные, необходимо построить график зависимости
Контрольные вопросы
1. Что называется теплоемкостью газа? 2. Какова размерность этой физической величины? 3. Что понимается под удельной и малярной теплоемкостями газа? 4. Как они связаны между собой? Какова связь между 5. Получите уравнение Роберт Майера. Сколько степеней свободы имеют молекулы газов Нe, Н2, СО2? 6. Какие это степени свободы? В каком газе показатель адиабаты 7. Почему в данном эксперименте целесообразно использовать сосуд возможно большего диаметра? 8. Получите уравнение адиабаты в перемененных PT и TV. Какие явления нарушают адиабатичность расширения газа? Вывод формулы для оценки значения
Ранее были введены обозначения
Воспользовавшись формулой бинома Ньютона и ограничиваясь двумя членами, получим:
Учитывая, что 4 и 5 лежат на одной изохоре, т.е.
Откуда
Поиск по сайту: |
 , показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины
, показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины 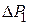 . Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t= 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7) снова записать показание манометра
. Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t= 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7) снова записать показание манометра  . Аналогично провести измерения для времени выдержки t=50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.
. Аналогично провести измерения для времени выдержки t=50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза. от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину
от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину  по формуле (11).
по формуле (11). В данной работе зависимость
В данной работе зависимость  статистически обрабатывается с помощью метода наименьших квадратов, который описан в приложении (возможно выполнение этой части программы в дисплейном классе на готовой программе).
статистически обрабатывается с помощью метода наименьших квадратов, который описан в приложении (возможно выполнение этой части программы в дисплейном классе на готовой программе). и
и  и числом степеней свободы молекул газа?
и числом степеней свободы молекул газа?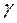 имеет наибольшее значение – N2, Нe, СН4?
имеет наибольшее значение – N2, Нe, СН4?
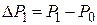 и
и 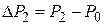 причем
причем  (см. рис.2). Запишем уравнение для адиабатического расширения газа (кривая 3-4):
(см. рис.2). Запишем уравнение для адиабатического расширения газа (кривая 3-4): или
или  .
. ;
;  .
. , можно записать:
, можно записать: .
.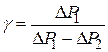 .
.