 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление относительной скорости
Обозначим m1 и m2 массы молекул первого и второго сорта газа, Тогда в выбранной системе координат
Дифференцируя эти равенства, получим
Здесь
С учетом теоремы умножения вероятности независимых событий, функция распределения молекул по скоростям есть произведение функций Максвелла
Соответственно в новых координатах (2) показатель степени запишется:
Таким образом, вероятность того, что система двух частиц имеет скорость в «объеме» пространства скоростей
Очевидно, что
Тогда искомая средняя относительная скорость равна
В случае молекул с одинаковыми массами m1 = m2 и
Лабораторная работа № 2-4 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ Цель работы: Изучить явление внутреннего трения в жидкостях. Задача работы: Определить коэффициенты внутреннего трения жидкостей методами вискозиметрии и Стокса. Теория Для наиболее общей характеристики свойств тел пользуются понятием агрегатных состояний – газообразного, жидкого и твердого. Благодаря большой разреженности вещества в газообразном состоянии его молекулы находятся сравнительно далеко друг от друга: на расстояниях, больших по сравнению с их собственными размерами. В газах молекулы не связаны между собой стационарными, устойчивыми связями. Молекулы постоянно изменяют относительные взаимные положения. Поэтому взаимодействие между молекулами газа играет второстепенную роль; большую часть времени молекулы движутся как свободные, лишь сравнительно редко испытывая столкновения друг с другом. В жидкостях же молекулы сближены на расстояния, сравнимые с их собственными размерами, они плотно заполняют занимаемое жидкостью пространство и сравнительно медленно меняют взаимное положение. В течение сравнительно продолжительных промежутков времени группы молекул могут образовывать агрегаты молекул. Эти агрегаты молекул по своим свойствам напоминают твердое тело, т.е. молекулы жидкостей находятся в сильном постоянном взаимодействии. В обычных условиях жидкости и газы настолько отличаются друг от друга по своей плотности, что различить их не представляет никакой трудности. Тем не менее, различие между этими двумя состояниями вещества в действительности не принципиальное, а лишь количественное – в количественной величине плотности и связанной с этим разнице в интенсивности взаимодействия молекул. Отсутствие принципиального отличия между ними в особенности ясно проявляется в том, что переход между состояниями, которые мы называем жидким и газообразным, может быть, в принципе, произведен вполне непрерывным образом, так что мы ни в какой момент не смогли бы указать, где кончилось одно состояние и началось другое. Количественный характер имеет также и различие между жидкостями и так называемыми аморфными (не кристаллическими) твердыми телами; к последним относятся стекло, различные смолы (например, канифоль) и т.п. и здесь отсутствие принципиальной разницы ясно проявляется в возможности непрерывного перехода из одного состояния в другое. В этом случае такой переход осуществляется путем простого нагревания. Так, твердое стекло при нагревании постепенно размягчается, становясь, в конце концов, вполне жидким; этот процесс совершенно непрерывен и в нем не существует никакого определенного «момента перехода». По своей плотности аморфное тело отличается от получающейся из него жидкости лишь незначительно. Основным количественным различием между ними является разница по величине их вязкости, т. е. в их «текучести». Общим свойством газов, жидкостей и аморфных твердых тел является беспорядочность распределения молекул в них. Эта беспорядочность обусловливает собой изотропию этих тел – одинаковость этих свойств по всем направлениям. Свойство изотропии принципиально отличает эти тела от анизотропных кристаллических твердых тел, в которых атомы расположены строго упорядоченным образом. Таким образом, из трех обычных состояний вещества (твердое, жидкое, газообразное) жидкости по своей структуре и межмолекулярным силам имеют как свойства газа, так и свойства твердых тел. Они занимают промежуточное положение. В жидкостях, как и в газах, наблюдаются явления диффузии, теплопроводности и вязкости. Однако механизм этих процессов в жидкостях иной, чем в газах. Явления переноса в газах определяются длиной свободного пробега молекул. Поэтому выражения для всех коэффициентов переноса содержат в качестве множителя длину свободного пробега молекул. В жидкостях, как и в очень плотных газах, понятие длины свободного пробега теряет смысл, так как среднее расстояние между молекулами сравнимо с размерами самих молекул. Молекулы жидкости могут лишь совершать малые колебания в пределах, ограниченных молекулярными расстояниями. Однако время от времени колеблющаяся молекула может получить от соседних молекул избыточную энергию, достаточную для того, чтобы совершить скачок на некоторое расстояние. Такие колебания, сменяющиеся скачками, представляют тепловое движение молекул жидкости. Ежесекундно молекула жидкости успевает переменить место около 108 раз, совершив между двумя последовательными переходами 103¸105 колебаний. Рассматривая протекающие в газах процессы, мы использовали понятие идеального газа. Идеальная жидкость, т.е. жидкость без трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается. Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости Наблюдается два вида течения жидкости (или газа). Если жидкость как бы разделена на слои, которые скользят друг относительно друга, не перемешиваясь, то течение называется ламинарным. Если в такой поток ввести подкрашенную струйку, то она сохранится, не размываясь по всей длине потока, так как в ламинарном потоке частицы жидкости не переходят из одного слоя в другой. Ламинарное течение стационарно. При увеличении скорости потока может наблюдаться перемешивание слоев жидкости. Такое движение называется турбулентным. При турбулентном течении скорость частиц в каждом данном месте все время изменяется беспорядочным образом – течение нестационарное. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места ее введения окрашенная жидкость равномерно распределится по всему сечению потока. Для выяснения закономерностей, которым подчиняются силы внутреннего трения, рассмотрим следующий опыт. Погрузим в жидкость две параллельные друг другу пластины (рис. 1). Пусть линейные размеры пластин значительно превосходят расстояние между пластинами ( Варьируя скорость пластины
где Нижняя пластина при движении верхней также оказывается подверженной действию силы Таким образом, при движении двух погруженных в жидкость пластин друг относительно друга между ними возникает взаимодействие, характеризуемое силой (1). Воздействие пластин друг на друга осуществляется, очевидно, через жидкость, заключенную между пластинами, передаваясь от одного слоя жидкости к другому. Если в любом месте зазора провести мысленно плоскость, параллельную пластинам (см. пунктирную линию на рис. 1), то можно утверждать, что часть жидкости, лежащая над этой плоскостью, действует на часть жидкости, лежащую под плоскостью, с силой
Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорость, как и сами пластины. Согласно формуле (2)
Используя равенство (3), формуле (1) для силы внутреннего трения можно придать вид
Величина Формула (4) была нами получена для случая, когда скорость изменяется по линейному закону (в этом случае градиент скорости является постоянным). Оказывается, что эта формула остается справедливой и для любого другого закона изменения скорости при переходе от слоя к слою. В этом случае для определения силы трения между двумя граничащими друг с другом слоями нужно брать значение градиента
где
т.е. возрастает пропорционально расстоянию поверхности раздела от оси трубы.
Из формулы (4) следует, что Единицей вязкости СИ является такая вязкость, при которой градиент скорости, равный 1м/с на 1 м, приводит к возникновению силы внутреннего трения в 1н на 1м2 поверхности касания слоев. Эта единица обозначается Динамическая вязкость жидкостей существенно зависит от температуры: с понижением температуры она увеличивается. Однако П.Л. Капицей было открыто, что жидкий гелий при температуре, близкой к абсолютному нулю (около –273 0С), переходит в особое состояние сверхтекучести, при котором вязкость резко падает, и становится меньше 10-13 Динамическая вязкость обычно не очень вязких жидкостей имеет порядок 10-3 Если ввести понятие касательного напряжения (
то выражение (4) примет вид
Преобразуем уравнение (8):
Из рис. 1 видно, что
Таким образом, скорость сдвига пропорциональна касательному напряжению и обратно пропорциональна коэффициенту вязкости жидкости. Для многих жидкостей коэффициент вязкости Для ньютоновских жидкостей реологическая кривая имеет вид прямой, проходящей через начало координат. Тангенс угла наклона ее равен коэффициенту вязкости жидкости (рис. 3, кривая 1). Жидкости, для которых реологическая кривая не является прямой линией, проходящей через начало координат (рис. 3, кривые 2, 3), не являются ньютоновскими.
Кроме динамической вязкости каждая жидкость может быть охарактеризована величиной кинематической вязкости. Отношение динамической вязкости Внутреннее трение является причиной того, что при протекании жидкости или газа через трубу требуется некоторая разность давлений. Эта разность давлений должна быть тем больше, чем больше коэффициент внутреннего трения. Зависимость между объемом
где Рассмотрим некоторые экспериментальные методы определения коэффициента внутреннего трения жидкостей. Метод вискозиметрии Как уже отмечалось, коэффициент вязкости жидкости можно определить, если измерить течение газа через трубу известных геометрических размеров, пользуясь формулой Пуазейля (10). Для такого опыта необходима труба, в которой течение жидкости будет ламинарным. При определенном значении скорости в жидкости начинают появляться вихри, что вызвано появлением составляющих скорости, перпендикулярных к оси трубы (для вихревого или турбулентного течения формула Пуазейля не справедлива). Одним из методов определения измерения коэффициента вязкости, основанным на использовании формулы Пуазейля, является метод капиллярного вискозиметра. Обоснование метода Формулой (9) удобно пользоваться для относительного определения коэффициента вязкости. Пусть через один и тот же капилляр протекают одинаковые объемы двух различных жидкостей (
Поделив уравнение (11) на (12), получим
Если жидкость вытекает под действием силы тяжести, то разность давлений равна гидростатическому давлению, т. е.
где
Поиск по сайту: |
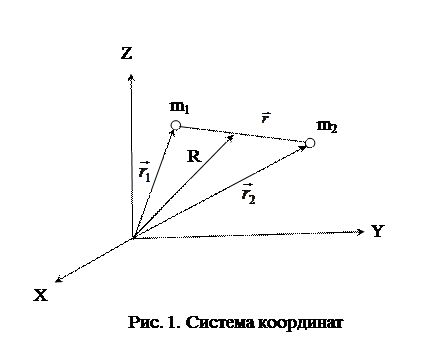 Фактически в газе все молекулы движутся с различными скоростями, причем скорости молекул подчиняются распределению Максвелла. Для того, чтобы учесть этот факт, оценим величину
Фактически в газе все молекулы движутся с различными скоростями, причем скорости молекул подчиняются распределению Максвелла. Для того, чтобы учесть этот факт, оценим величину  относительной скорости двух молекул, движущихся со скоростями
относительной скорости двух молекул, движущихся со скоростями  и
и  . Эту задачу удобнее решать в системе центра масс.
. Эту задачу удобнее решать в системе центра масс. и
и  – радиусы-векторы первой и второй молекул.
– радиусы-векторы первой и второй молекул.  – расстояние между молекулами, R – радиус-вектор центра масс (рис. 1).
– расстояние между молекулами, R – радиус-вектор центра масс (рис. 1). .
.

 -скорость центра масс системы двух частиц,
-скорость центра масс системы двух частиц,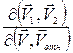 =1 (доказать), следовательно
=1 (доказать), следовательно .
.
 .
.

 где
где  – масса системы;
– масса системы;  –приведенная масса.
–приведенная масса.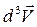 и
и  равна
равна .
. - вероятность для скорости всей системы, а
- вероятность для скорости всей системы, а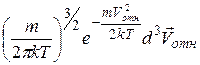 - вероятность для относительной скорости молекул.
- вероятность для относительной скорости молекул. .
.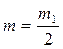 , поэтому
, поэтому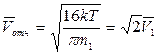 .
. как функцию времени. Величина и направление вектора
как функцию времени. Величина и направление вектора  ). Нижнюю пластину закрепим на месте. Верхнюю пластину приведем в движение с некоторой скоростью
). Нижнюю пластину закрепим на месте. Верхнюю пластину приведем в движение с некоторой скоростью  относительно нижней. Для перемещения верхней пластины с постоянной скоростью
относительно нижней. Для перемещения верхней пластины с постоянной скоростью  . Поскольку верхняя пластина движется равномерно со скоростью
. Поскольку верхняя пластина движется равномерно со скоростью 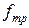 .
. и расстояние между ними
и расстояние между ними  , (1)
, (1) - коэффициент пропорциональности, зависящий от природы и состояния (например, температуры) жидкости и называемый коэффициентом внутреннего трения или коэффициентом вязкости, или просто вязкостью жидкости (газа).
- коэффициент пропорциональности, зависящий от природы и состояния (например, температуры) жидкости и называемый коэффициентом внутреннего трения или коэффициентом вязкости, или просто вязкостью жидкости (газа). , равной по величине
, равной по величине  .
. Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении
Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении 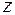 , перпендикулярном к пластинам (рис. 1), по линейному закону
, перпендикулярном к пластинам (рис. 1), по линейному закону . (2)
. (2) . (3)
. (3) . (4)
. (4) показывает, как быстро изменяется скорость в направлении оси
показывает, как быстро изменяется скорость в направлении оси 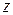 , и называется градиентом скорости (точнее, это – модуль градиента скорости; сам градиент – вектор).
, и называется градиентом скорости (точнее, это – модуль градиента скорости; сам градиент – вектор). , (5)
, (5) - радиус трубы,
- радиус трубы,  - скорость на расстоянии
- скорость на расстоянии  от оси трубы (рис. 2). Проведем в жидкости мысленно цилиндрическую поверхность радиуса
от оси трубы (рис. 2). Проведем в жидкости мысленно цилиндрическую поверхность радиуса  . Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга, с силой, величина которой в расчете на единицу поверхности равна
. Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга, с силой, величина которой в расчете на единицу поверхности равна , (6)
, (6) Коэффициент пропорциональности
Коэффициент пропорциональности  (эта) характеризует вязкость жидкости и называется коэффициентом динамической вязкости или просто вязкостью жидкости.
(эта) характеризует вязкость жидкости и называется коэффициентом динамической вязкости или просто вязкостью жидкости.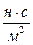 или Па×с. (в системе СГС коэффициент вязкости измеряется в Пуазах по имени французского ученого Пуазейля, 1Пз = 0,1 Н с/м2).
или Па×с. (в системе СГС коэффициент вязкости измеряется в Пуазах по имени французского ученого Пуазейля, 1Пз = 0,1 Н с/м2). , т. е. практически равна нулю. Это значит, что жидкий гелий может свободно протекать через самые тонкие капилляры, щели и отверстия, непроницаемые даже для газа.
, т. е. практически равна нулю. Это значит, что жидкий гелий может свободно протекать через самые тонкие капилляры, щели и отверстия, непроницаемые даже для газа. )
)
 , (7)
, (7) . (8)
. (8) .
. , откуда
, откуда . (9)
. (9) Вязкость ньютоновских жидкостей при постоянной температуре и давлении не остается постоянной, а зависит от скорости сдвига, от времени действия напряжения.
Вязкость ньютоновских жидкостей при постоянной температуре и давлении не остается постоянной, а зависит от скорости сдвига, от времени действия напряжения. называется коэффициентом кинематической вязкости
называется коэффициентом кинематической вязкости 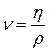 . Коэффициент кинематической вязкости измеряется в
. Коэффициент кинематической вязкости измеряется в  или в Стоксах – 1 Ст = 10-4 м/с.
или в Стоксах – 1 Ст = 10-4 м/с. жидкости (или газа), протекающей в единицу времени через сечение трубы, и разностью давлений
жидкости (или газа), протекающей в единицу времени через сечение трубы, и разностью давлений  на концах трубы устанавливается известной формулой Пуазейля:
на концах трубы устанавливается известной формулой Пуазейля: (10)
(10) - длина трубы,
- длина трубы, 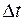 и разность давлений на ее концах, определить коэффициент вязкости жидкости.
и разность давлений на ее концах, определить коэффициент вязкости жидкости. ). Тогда объемы первой и второй жидкостей, как следует из формулы Пуазейля, будут равны:
). Тогда объемы первой и второй жидкостей, как следует из формулы Пуазейля, будут равны: (11)
(11) (12)
(12) . (13)
. (13)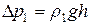 ,
, 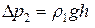 , (14)
, (14) и
и 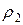 – плотность жидкости при температуре опыта. Подставляя (14) в (13), получим
– плотность жидкости при температуре опыта. Подставляя (14) в (13), получим
 ;
;  . (15)
. (15)