 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Среднее квадратичное отклонение, дисперсия и их свойства
В качестве показателя размера вариации вариант в статистике принято среднее квадратичное отклонение S. Для его вычисления все отклонения возводятся в квадрат, потом вычисляется среднее из полученных квадратов - средний квадрат отклонений, а затем из этого среднего извлекают корень. В экспериментальных распределениях при определении среднего квадрата квадраты отклонений делятся на (N - 1)
Дисперсия распределения D:
Формулу дисперсии (8) легко представить в другом виде, более удобном для вычисления Свойства дисперсии и среднего квадратичного отклонения: 1. Если все значения вариант увеличить на одну и ту же величину а, то на ту же величину а увеличивается их среднее арифметическое. Отклонения же останутся без изменения. Значит, останутся без изменения дисперсия и среднее квадратичное отклонение. 2. Если все значения вариант умножить на одно и то же число К, то в К раз увеличится их среднее арифметическое 3. Средняя величина квадратов отклонений вариант от любой величины а, больше дисперсии D. на квадрат отклонения этой величины а от среднего арифметического вариант. 4. Если совокупность разбита на несколько частей, то общая дисперсия является суммой средней величины дисперсии внутри отдельных частей совокупности Di и среднего квадрата отклонения частных средних от общей средней
 .
Мода Важным показателем характеристики распределения является мода. Мода - это наиболее часто встречающееся значение варианты. Мода - это значение варианты, которой соответствует наибольшая относительная частота. Асимметрия и эксцесс
Гистограммы распределений изучаемых статистических совокупностей довольно часто бывают асимметричными (рис.3, 4), Если среднее арифметическое лежит правее моды, то асимметрия положительная, если левее моды - отрицательная. Для статистической оценки распределения необходимо вычислять меру асимметрии, называемую коэффициентом асимметрии  вычисления. В основу коэффициента асимметрии положено среднеквадратичное отклонение, которое даёт возможность более полно учесть крайние значения вариант. При наличии асимметрии одна сторона кривой дает большее кубическое отклонение, чем другая, и так как знак при кубическом отклонении сохраняется, то разница между суммами кубических отклонений показывает положительную либо отрицательную асимметрии.
ЕслиЕ > 1 , то эксцесс положительный и вершина кривой будет выше нормальной, и наоборот, если Е < 1 , то эксцесс отрицательный, вершина кривой ниже нормальной (рис.5).
Поиск по сайту: |
.
.
.
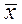, отклонения от среднего арифметического 
- 
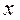2
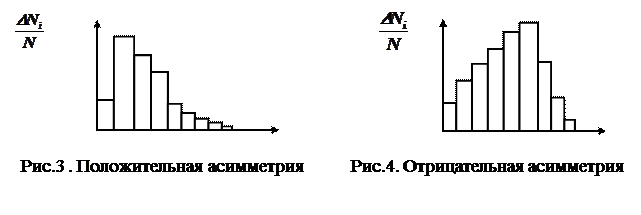
Наряду с асимметрией при статистическом анализе рядов распределения, важное значение имеет мера эксцесса. Мера эксцесса - это показатель отличия данного распределения от нормального по концентрации вариант около центра распределения. Вычисление этого показателя делается для того, чтобы определить, насколько кривая, полученная из опыта, оказывается более плоской и растянутой, или, наоборот, более сжатой и выпуклой в центре по сравнению с кривой нормального распределения. Показатель эксцесса выражается следующей формулой:
.