 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоретическое распределение дискретной и непрерывной случайной величины
Дискретное распределение считается теоретически заданным, если известны все возможные значения
При дискретном распределении общая масса вероятности, равная единице, сосредоточена в счетной или конечной системе точек хi . Другими словами, точечное распределение массы вероятности, подобно, например, точечному распределению электрических зарядов. К теоретическим распределениям дискретных величин относятся биномиальное, гипергеометрическое, распределение Пуассона. Каждое из этих распределений описывается аналитической функцией, выражающей зависимость вероятности от дискретной переменной величины и параметров распределения. Функция биноминального распределения:
где q = 1 – p, n, p - параметры распределения. Функция распределения Пуассона
где l - параметр распределения. Для теоретического изучения распределения непрерывных величин вводится понятие плотности вероятности
где Dx длина малого интервала, начинающегося в точке x Для бесконечно малого интервала Dx вероятность
для конечного интервала
Интеграл от плотности вероятности распределения по любому промежутку оси дает вероятность попадания величины X в этот промежуток Dx. Плотностью распределения может служить любая интегрируемая функция
Вероятность
называется интегральной функцией распределения в отличие от плотности вероятности Графическое представление дифференциальной функции распределения
1. P(x)- непрерывная возрастающая функция: её приращение в промежутке
т.е. и следовательно
3. Производная от интегральной функции распределенная P(x) равна плотности
Параметры теоретического распределения
Поиск по сайту: |
 , принимаемые величиной, и вероятности
, принимаемые величиной, и вероятности  для каждого события в поле испытаний. Так как эти события должны образовывать полную группу, то полная вероятность
для каждого события в поле испытаний. Так как эти события должны образовывать полную группу, то полная вероятность .
.
 ,
,
 ,
,

 ,
,
 , (13)
, (13) , где
, где  ,
,
 , удовлетворяющая двум условиям:
, удовлетворяющая двум условиям: ,
,
 .
.

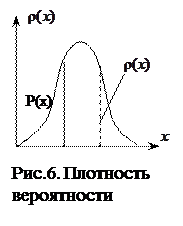 На графике (рис.6) плотность вероятности
На графике (рис.6) плотность вероятности 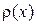 является ординатой кривой распределения, а вероятность Р(х) равна площади под этой кривой oт -¥ до x. По определению Р(x) обладает следующими свойствами:
является ординатой кривой распределения, а вероятность Р(х) равна площади под этой кривой oт -¥ до x. По определению Р(x) обладает следующими свойствами: равно вероятности для величины X попасть в этот промежуток. В самом деле, по правилу сложения вероятностей:
равно вероятности для величины X попасть в этот промежуток. В самом деле, по правилу сложения вероятностей: ,
,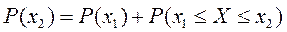 ,
,
 .
. ,
,
 .
.
 .
.