Параметрические критерии различия

Параметрические критерии позволяют установить совпадение или различие между параметрами двух распределений - их средними значениями, дисперсиями, коэффициентами асимметрии, эксцесса и т.д. При пользовании параметрическими критериями обычно предполагается, что сравниваемые распределения в общем однотипны и могут отличаться лишь значениями своих параметров.

Из-за случайности в образовании выборки распределения вариант в выборке всегда отличаются от их распределения в генеральной совокупности; поэтому если в генеральной совокупности варианты распределены по определенному теоретическому закону, то распределение в выборке будет заведомо отклоняться от этого закона. Отсюда следует, что сам факт отклонения выборочного распределения от того или иного теоретического распределения еще не дает основания утверждать, что и в генеральной совокупности распределение не подчиняется данному теоретическому закону. Таким образом, вопрос сводится к тому, можно ли расхождение между выборочным и предположенным теоретическим распределением отнести за счет расхождения между выборкой и генеральной совокупностью, или же оно является результатом того, что сама генеральная совокупность отклоняется от данного теоретического распределения

В любом случае задача может быть сведена к проверке гипотезы об отсутствии реального различия. Эту гипотезу называют нулевой гипотезой. Предельно допустимое значение вероятности, начиная с которого вероятность можно считать малой, называют уровнем значимости. 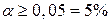Если вероятность нулевой гипотезы a<1% , то она отвергается, если вероятность лежит в пределах от 1% до 5%, то возможность отвергнуть нулевую гипотезу сомнительна, если же , то нулевая гипотеза принимается. Выбор уровня значимости определяется в различных случаях конкретными задачами исследования.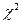

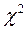2. Критерий соответствия

К.Пирсон предложил критерий (хи-квадрат) для оценки степени различия двух сравниваемых рядов частостей (можно сравнивать эмпирический и теоретический или два эмпирических распределения). Этот критерий представляет собой сумму отношений квадратов разностей между частостями эмпирического и теоретического распределений к частостям (вероятностям) теоретического распределения:

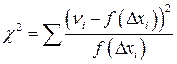, (29)

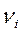где - частость эмпирического распределения, 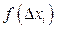- вероятность теоретического распределения.

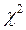Чтобы дать правило проверки, следует выбрать уровень значимости для критерия. Определив значение по данным выборки, нужно его сопоставить с критическим значением , соответствующим выбранному уровню значимости. Если 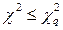, то расхождение между экспериментальным и теоретическим распределением несущественно, и экспериментальное распределение можно аппроксимировать теоретическим.

Поиск по сайту: