 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Опыт Боте. Фотоны. Давление света
Для объяснения распределения энергии в спектре равновесного теплового излучения достаточно, как показал Планк, допустить, что свет только испускается порциями hv. Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями. Однако Эйнштейн пошел значительно дальше. Он выдвинул гипотезу, что свет и распространяется в виде дискретных частиц, названных первоначально световыми квантами. Впоследствии эти частицы получили название фотонов. Гипотеза Эйнштейна была подтверждена рядом опытов. Наиболее непосредственное подтверждение дал опыт Боте. Тонкая металлическая фольга Ф (рис. 7) помещалась между двумя газоразрядными счетчиками Сч.
равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были бы срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении. Итак, было экспериментально доказано существование особых световых частиц – фотонов. Фотон обладает энергией
e =
определяемой только его частотой v или длиной волны l. Подстановка значений и и с приводит к формуле (9): lмин = 12390/U где U выражена в электрон-вольтах, а l в ангстремах. Длине волны l = 0,555 мкм = 5550 А соответствует энергия фотона e = 2,23 эв. Для рентгеновских лучей (l = 10-4…103 А) энергия фотона лежит в пределах от 15 эвдо 100 Мэв. Согласно теории относительности частица с энергией e обладает массой m = e/c2. Подставив значение e, получим для массы фотона выражение:
m =
Фотон есть частица, движущаяся со скоростью с. Подстановка в формулу
p = e/c =
Учтя, что 2p/l равно волновому числу k,т. е. модулю волнового вектора k, импульс фотона можно записать в векторном виде:
p =
Из наличия у фотона импульса вытекает, что свет, падающий на какое-либо тело, должен оказывать на это тело давление, равное импульсу, сообщаемому фотонами единице поверхности в единицу времени. Пусть плотность потока фотонов (число фотонов, падающих на единицу поверхности в единицу времени) равна N. Если все фотоны поглощаются телом, давление равно Р = рN = eN/c. При условии, что все фотоны отражаются телом в обратном направлении, давление будет в два раза больше: Р = 2рN = 2eN/c. Наконец, если отражается доля фотонов, равная r (r – коэффициент отражения), и поглощается доля, равная (1 – r), для давления получится выражение:
P = 2erN/c + e(1 – r)N/c = (1 + r)eN/c. (15) Плотность потока фотонов N можно представить как произведение плотности фотонов n (т. е. количества фотонов в единице объема) на их скорость с,т. е. N = nc. Далее, замечая, что произведение ne дает энергию фотонов, заключенных в единице объема, w(плотность энергии), можно написать: P = (1 + r)w, что совпадает с выражением, полученным в рамках электромагнитной теории.
Эффект Комптона
Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны l,содержатся также лучи большей длины волны l¢. Разность Dl = (l¢ – l) оказалась независящей от l, и от природы рассеивающего вещества. Экспериментально была установлена следующая закономерность:
Dl = (l¢ – l) = l0(1 – cosq), (16)
где q угол, образуемый направлением рассеянного излучения с направлением первичного пучка, l0 – постоянная, равная 0,0242 А.
Кривая ахарактеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния q, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс – величина, пропорциональная длине волны. Рис. 10 характеризует зависимость соотношения интенсивностей смещенной М и несмещенной Р компонент от атомного номера рассеивающего вещества. Верхняя кривая в левом столбце характеризует первичное излучение (линия Касеребра). При рассеянии веществами с малым атомным номером (Li, Be, В) практически все рассеянное излучение имеет смешенную длину волны. По мере увеличения атомного номера все большая часть излучения рассеивается без изменения длины волны.
Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать наиболее слабо связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении. Пусть на первоначально покоящийся свободный электрон падает фотон с энергией
Рис. 11
изображен на рис. 11. Из законов сохранения энергии и импульса можно вывести соотношение Dl = (l¢ – l) = 2p Величина
L = 2p
носит название комптоновской длины волны. Подстановка численных значений для электрона дает значение 3, 86 10-11 см или после умножения на 2p значение l0 = 0,0242 А, что хорошо согласуется со значением в эмпирической формуле (16). При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Так как масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно мало. По мере роста атомного номера увеличивается относительное число электронов с сильной связью, чем и обусловливается ослабление смещенной линии (рис, 10).
Фотолюминисценсия
Некоторые тела при освещении не только отражают часть падающего на них света, но и начинают светиться. Такое свечение, или люминесценция, отличается важной особенностью: свет люминесценции имеет иной спектральныйсостав, чем свет, вызвавший свечение. Примером легко наблюдаемой люминесценции может служить синевато-молочное свечение керосина, рассматриваемого на дневном свету. Очень большое число растворов красок и других веществ обнаруживают люминесценцию, особенно под действием источников, испускающих ультрафиолетовый свет (например, электрической дуги или ртутной лампы). Свечение такого рода называют фотолюминесценцией, желая подчеркнуть, что оно возникает под действием света. Изменение цвета свечения по сравнению с цветом возбуждающего света нередко заметно на глаз. Еще лучше наблюдается указанная особенность, если сравнить спектр света люминесценции со спектром возбуждающего света. Все эти наблюдения показывают, что: свет люминесценции характеризуется большей длиной волны, чем свет возбуждающий, что называется правилом Стокса. Ключ к пониманию правила Стокса дают квантовые представления. Вообразим, что свечение вызывается монохроматическим светом частоты ν. Таким образом, молекула люминесцирующего вещества поглощает энергию в виде кванта hν. Процессы, вызываемые поглощенной энергией в молекуле, довольно сложны. Часть энергии кванта расходуется на эти процессы, а часть вновь испускается в виде света люминесценции. Испускаемый квант должен, следовательно, иметь меньшую энергию, т.е. соответствовать меньшей частоте ν'. Это уменьшение частоты (увеличение длины волны) и составляет содержание правила Стокса. Применяя источники света, содержащие значительное количество коротких (ультрафиолетовых) лучей, можно обнаружить, что почти все тела обладают способностью в большей или меньшей степени люминесцировать. Нередко удаётся значительно усилить люминесценцию, сильно охладив тело, например, погрузив его в жидкий воздух. Некоторые тела сохраняют способность светиться некоторое время после того, как освещение их прекратилось. Такое послесвечение может иметь различную длительность. В некоторых объектах оно продолжается очень малое время (десятитысячные доли секунды и меньше). В других оно тянется много секунд и даже минут (часов), так что наблюдение его не представляет никаких трудностей. Принято называть свечение, прекращающееся вместе с освещением, флюоресценцией, а свечение, имеющее заметную длительность – фосфоресценцией. Явление длительной фосфоресценции обнаруживают многие специально приготовленные кристаллические порошки. Ими пользуются для изготовления, так называемых фосфоресцирующих экранов. Лист картона, покрытый, например, порошком сернистого цинка, представляет хороший фосфоресцирующий экран, сохраняющий свое свечение две-три минуты после освещения. Такие экраны светятся и под действием рентгеновских лучей. Следует отметить, впрочем, что явление люминесценции под действием рентгеновских лучей более сложно, чем под действием обычного света, ибо при этом играют роль быстрые электроны, вырываемые рентгеновскими лучами. Очень важное применение нашли в последнее время фосфоресцирующие порошки при изготовлении ламп дневного света. В газосветных лампах свечение, возникающее при электрическом токе в газе, например в парах ртути, обычно содержит много ультрафиолетового света, не только не пригодного для освещения, но и вредного для глаза. Покрывая внутренность таких ламп специально изготовленным фосфоресцирующим составом, удалось превратить этот ультрафиолетовый свет в видимый (в согласии с правилом Стокса). Это приводит к большой экономии электроэнергии, ибо в таких лампах в энергию видимого света превращается примерно в три раза большая доля электрической энергии, чем в лампочках накаливания. Подбирая состав фосфоресцирующего вещества, можно добиться также и улучшения спектрального состава излучаемого света, приближая его к спектральному составу дневного света. Так устроены современные лампы дневного света. Кроме упомянутого уже применения люминесценции для фосфоресцирующих экранов и различных светящихся красок для декоративных и театральных целей необходимо отметить еще одну важную область применения ее. Явления люминесценции характеризуются крайне высокой чувствительностью: достаточно иногда располагать 10-10 гсветящегося вещества, например, в виде раствора, чтобы иметь возможность обнаружить его по характерному свечению. Возможно наблюдение при помощи люминесценции ничтожных следов вещества, составляющего миллионную долю процента в какой-нибудь смеси. Эта высокая чувствительность делает люминесценцию важным средством обнаружения некоторых ничтожно малых примесей, позволяющим судить о каких-либо загрязнениях или процессах, приводящих к изменению исходного вещества. При помощи люминесценции можно обнаружить самые начальные стадии загнивания продуктов. Известны применения люминесцентного анализа при разведке нефти. Если почва, извлекаемая при бурении, содержит ничтожные следы нефти, то их можно легко обнаружить по флюоресценции. Таким образом, удается судить о близости нефтеносных слоев. Существует и много других областей технического применения люминесцентного анализа.
Выше был рассмотрен ряд явлений, в которых свет ведет себя как поток частиц (фотонов). Однако такие явления, как интерференция и дифракция света, могут быть объяснены только на основе волновых представлений. Таким образом, свет обнаруживает корпускулярно-волновой дуализм (двойственность): в одних явлениях проявляется его волновая природа и он ведет себя как электромагнитная волна, в других явлениях проявляется корпускулярная природа света и он ведет себя как поток фотонов.
Лекция 7
Поиск по сайту: |
 Рис. 7.
Рис. 7.
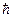 w = 2p
w = 2p  значения v= с обращает знаменатель формулы в нуль. Вместе с тем, как мы видели, масса фотонаконечна. Это возможно только в том случае, если масса покоя фотона m0 = 0. Таким образом, фотон это особая частица, отличающаяся от других, имеющих не нулевую массу покоя. Не имея массы покоя, фотон может существовать только двигаясь со скоростью света. Положив в формуле
значения v= с обращает знаменатель формулы в нуль. Вместе с тем, как мы видели, масса фотонаконечна. Это возможно только в том случае, если масса покоя фотона m0 = 0. Таким образом, фотон это особая частица, отличающаяся от других, имеющих не нулевую массу покоя. Не имея массы покоя, фотон может существовать только двигаясь со скоростью света. Положив в формуле  m0 = 0, получим Е = ср, откуда следует, что фотон обладает импульсом –
m0 = 0, получим Е = ср, откуда следует, что фотон обладает импульсом – Рис. 8.
Рис. 8.

 Рис. 9.
Рис. 9.
 Рис. 10.
Рис. 10.
