|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифракция Фраунгофера от щели
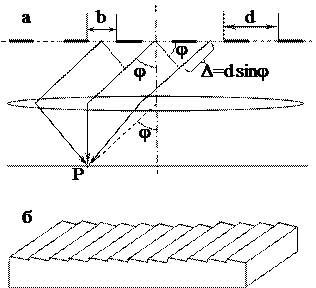
Рассмотрим плоскую световую волну, падающую на длинную щель за которой расположены цилиндрическая собирающая линза и экран в ее фокальной плоскости, как это изображено на рис. 9, а (направление щели и ось линзы перпендикулярны плоскости рисунка). Вторичные волны, посылаемые отдельными точками в направлении, определяемом углом j, соберутся в некоторой точке экрана Р. Амплитуды отдельных колебаний равны, а разность фаз D для двух указанных на рис. 9 а точек О и А будет определяться отрезком АВ, так как оптические пути ОР и ВР одинаковы.
а б
Рис. 9. направлении собравшись на экране дадут темную полосу. Условие для углов при которых амплитуда на экране обращается в 0 запишется:
b sinj = ±kl (k = 1, 2, 3…). (11)
Общий вид распределения интенсивности в зависимости от синуса угла наблюдения приведен на рис. 10.
Дифракционная решетка
Дифракционная решетка представляет собой совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей (рис. 11, а). Расстояние dмежду серединами соседних щелей называется периодом решетки. Число щелей на 1 мм решетки может достигать 1000, а общее число – 100000. Широкое применение находят отражательные решетки, которые получают нанося на отполированную поверхность металла параллельные штрихи тонким алмазным резцом (рис.11, б).
Рис. 11. Рис. 12 Расположим параллельно решетке собирательную линзу, в фокальной плоскости которой поставим экран. Выясним характер дифракционной картины, получающейся на экране при падении нормально на решетку плоской световой волны. Каждая из щелей даст на экране картину, описываемую кривой, изображенной на рис. 10, при этом для направлений, определяемых условием:
d sinj = ±ml, (m= 0, 1, 2, ...) (12)
колебания от отдельных щелей будут взаимно усиливать друг друга, вследствие чего амплитуда колебаний в соответствующих точках экрана будет иметь максимумы. Формула (12) называется формулой дифракционной решетки и определяет направления на главные максимумы интенсивности для соответствующих длин волн. Положение главного максима нулевого порядка (m = 0) для всех длин волн совпадает. Примерный вид дифракционной картины приведен на рис. 12. В соответствии с (12) при уменьшении периода решетки d синусы углов на соседние максимумы будет увеличиваться, а направления для максимумов более длинных волн при данном периоде решетки (красных) будут дальше от направления падения света.
Дисперсия света
Из теории Максвелла следует, что в вакууме все электромагнитные волны независимо от их частоты (длины волны) распространяются с одной и той же скоростью с, что подтверждает опыт. Однако оказывается, что показатель преломления (n = с/ссред) вещества зависит от частоты колебаний световой волны и тем самым от длины волны. Но если показатель преломления зависит от частоты, то и скорость распространения света в веществе также зависит от частоты. Зависимость скорости волны от ее частоты (или длины волны) называют дисперсией. Результатом дисперсии является спектральное разложение белого света при его преломлении в призме (рис. 13). Рассмотрим белый свет, падающий из вакуума (воздуха) на одну из граней призмы, изготовленной из стекла флинт под углом iпад = 60°. Показатели преломления для разных длин волн и разных стекол даны в таблице. Таблица
Углы преломления в соответствии с законом Снеллиуса (формула 2 лекции 1) составляют для этих цветов rкр = 31°48', rзел = 31°28' и rф = 30°55'. После преломления на второй грани лучи выйдут из призмы под соответствующими углами r¢ : r¢кр = 50°28', r¢зел = 52°18', r¢ф = 55° (рис. 13).
Рис. 13. Рис. 14.
Данное явление разложение белого света в спектр за счет дисперсии используют в призматических спектроскопах. Зависимость показателя преломления n от частоты колебаний электромагнитной волны (дисперсионная кривая),показана на рис. 14 сплошной линией. Наиболее резкие изменения показателя преломления происходят вблизи резонансных частот, т. е. в тех случаях, когда частота электромагнитной волны совпадает с одной из собственных частот колебаний электронного облака атома. Вдали от резонансных частот показатель преломления возрастает с ростом частоты электромагнитной волны, вблизи же резонансной частоты наблюдается резкий спад показателя преломления с ростом частоты. Для объяснения явления дисперсии пользуются электронными представлениями строения вещества. Под действием электромагнитной волны электронное облако атома (или молекулы) совершает вынужденные колебания, следовательно, атом превращается в миниатюрный электрический диполь. Электрический момент этого атомарного диполя совершает вынужденные колебания с частотой, равной частоте колебаний напряженности поля, и с амплитудой, зависящей от соотношения между частотой колебаний электромагнитного поля и собственной частотой электронного облака. Но при разных амплитудах электрический момент атомарного диполя различен. В результате разным частотам колебаний напряженности поля соответствуют разные значения показателя преломления, что и приводит к дисперсии.
Поглощение света
Как уже отмечалось, электромагнитные волны (в том числе и свет), проходя через вещество, вызывают вынужденные колебания электронного облака атомов или молекул. Тем самым вещество поглощает часть энергии волны и интенсивность последней по мере проникновения в глубь вещества уменьшается. Поглощениесвета – это затухание колебаний световой волны, обусловленное ее взаимодействием с веществом. Очевидно, что степень поглощения света зависит от толщины d слоя вещества. Если обозначить I0 интенсивность световой волны до попадания в вещество, а I – ее интенсивность после прохождения слоя вещества толщиной d,то справедлива следующая закономерность:
I = I0 exp(–md), (13)
где m – коэффициент поглощения, называемая законом Бугера. Коэффициент поглощения m зависит от частоты волны; иными словами, наряду с дисперсией коэффициента преломления имеется дисперсия коэффициента поглощения. На рис. 14 пунктирной кривой показана зависимость коэффициента поглощения m от частоты со. Как видно, максимально вещество поглощает свет вблизи собственной частоты. Данное явление есть следствие общего свойства вынужденных колебаний: система поглощает наибольшую мощность при резонансе. У атомов и молекул имеется не одна собственная частота, а набор собственных частот вблизи каждой из который коэффициент поглощения резко возрастает. В твердых телах или растворах из-за сильного взаимодействия между атомами или молекулами области поглощения уширяются и превращаются в полосы поглощения, между ними лежит область частот, которые поглощаются слабо. На этом основано действие светофильтров, которые представляют собой пластины из стекла с присадками тех или иных солей, пленки из пластмасс, содержащие некоторые органические красители или растворы красителей в воде, спирте и других растворителях. В зависимости от химического состава светофильтр пропускает только определенную область частот, поглощая остальные. Избирательным поглощением света объясняется цвет тела. Если тело почти полностью отражает в одинаковой мере все падающие на него лучи, то при освещении его белым светом оно видно как белое. Освещенное светом одного цвета (монохроматическим светом), такое тело отражает его и кажется окрашенным в тот же цвет. Точно так же ведет себя сероетело, оно лишь поглощает часть света на всех участках спектра одинаково. Черным называют тело, которое практически полностью поглощает все световые волны видимого участка спектра. Если тело избирательно поглощает некоторые участки спектра, то в отраженном свете оно кажется цветным. Пусть, например, тело сильно поглощает сине-зеленый участок спектра, тогда, если осветить его белым светом, оно отразит красно-оранжевый участок спектра, и мы увидим тело красным. Нетрудно сообразить, что если это тело осветить синим светом (или зеленым), то оно будет выглядеть как черное. Опыт подтверждает этот результат. Лекция 5 Поляризованный свет
На первой лекции говорилось, что в естественном свете колебания вектора Епроисходит хаотично в произвольных направлениях. Если каким либо способом упорядочить эти колебания, то получится свет поляризованный. В зависимости от того как упорядочены эти колебания, можно выделить свет поляризованный линейно (плоско), поляризованный по кругу и по эллипсу. В первом случае, который мы будем рассматривать более подробно, колебания вектора Е происходят в одной плоскости. Во втором и третьем случаях конец вектора Е движется по кругу и эллипсу соответственно. Для плоско поляризованного света плоскость, в которой происходят колебания вектора Е, называется плоскостью колебаний, а перпендикулярная ей плоскость – плоскостью поляризации. Устройства, с помощью которых можно получить плоско поляризованный свет, называются поляризаторами. Эти устройства пропускают свет с колебаниями в одной плоскости, которую называют плоскостью поляризатора. Поляризатор может быть не идеальным, тогда свет, прошедший через него будет поляризован частично. Для частично поляризованного света можно ввести понятие степени поляризации Р:
Р = (Iмакс – Iмин)/(Iмакс + Iмин), (1)
где Iмакс – максимальное значение интенсивности света пропущенного через идеальный поляризатор, а Iмин – соответственно его минимальное значение при перпендикулярном положении плоскости поляризатора. Для поляризованного света Iмин = 0 и Р = 1. Рассмотрим плоско поляризованный свет, прошедший через поляризатор П1 и падающий на поляризатор П2, плоскость пропускания которого расположена под углом j к плоскости колебаний, рис. 1, а.
Рис. 1.
Если амплитуду колебаний Е разложить на две составляющие: параллельную (Е÷÷) и перпендикулярную (Е^) плоскости поляризатора, то вероятно через поляризатор пройдет компонента Е÷÷., рис. 1, б. Поскольку Е÷÷.= Еcosj, для интенсивности прошедшего света будем иметь (I ~ Е2):
I = I0 cos2j. (2)
Соотношение (2) носит название закона Малюса. Если на поляризатор падает естественный свет, плоскости колебания в котором имеют хаотическое распределение, то интенсивность поляризованного света, прошедшего через поляризатор будет равна ½ Iест, поскольку среднее значение cos2j за период равно ½. Если на пути этого света поставить второй поляризатор, то в соответствии с (2) интенсивность света будет меняться от ½ Iест до 0. В последнем случае говорят, что поляризаторы скрещены, то есть плоскости их пропускания перпендикулярны.
Поиск по сайту: |
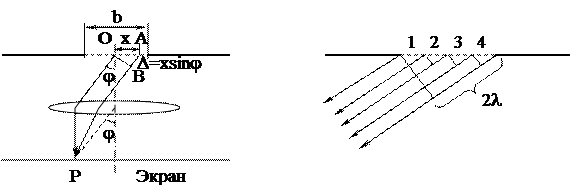 Рассмотрим направление, для которого, например, разность хода крайних лучей будет кратна длине волны D = kl. На рис. 9, б приведен случай, когда k = 2. В этом случае действие соседних зон будет компенсировать друг друга и следовательно лучи, идущие в этом
Рассмотрим направление, для которого, например, разность хода крайних лучей будет кратна длине волны D = kl. На рис. 9, б приведен случай, когда k = 2. В этом случае действие соседних зон будет компенсировать друг друга и следовательно лучи, идущие в этом Рис. 10.
Рис. 10.