 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Явление вращения плоскости поляризации
3.1. Естественное вращение.Оптически активные среды
Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них плоско-поляризованного света. К числу таких веществ принадлежат кристаллические тела (например, кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, винной кислоты и др.). Кристаллические вещества сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптической оси кристалла. Угол поворота j пропорционален пути l, пройденному лучом в кристалле:
j = al. (4)
Коэффициент a называют постоянной вращения. Эта постоянная зависит от длины волны (дисперсия вращательной способности). В растворах угол поворота плоскости поляризации пропорционален пути света в растворе l и концентрации активного вещества С:
j = [а] Сl. (5)
Здесь [а] – величина, называемая удельной постоянной вращения. В зависимости от направления вращения плоскости поляризации оптически активные вещества подразделяются на право- и левовращающие. Направление вращения (относительно луча) не зависит от направления луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл еще раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации. Все оптически активные вещества существуют в двух разновидностях: правовращающей и левовращающей. Существуют право- и левовращающий кварц, право- и левовращающий сахар и т. д. Молекулы или кристаллы одной разновидности являются зеркальным отражением молекул или кристаллов другой разновидности (рис. 5).
Если между двумя скрещенными поляризаторами поместить оптически активное вещество (кристалл кварца, прозрачную кювету с раствором сахара и т п.), то поле зрения просветляется. Чтобы снова получить темноту, нужно повернуть один из поляризаторов на угол j, определяемый выражением (4) или (5). В случае раствора, зная удельную постоянную вращения [а] данного вещества и длину l, можно, измерив угол поворота j, определить по формуле (5) концентрацию раствора С. Такой способ определения концентрации применяется в производстве различных веществ, в частности в сахароварении, соответствующий прибор называется сахариметром (рис. 6) . 3.2. Магнитное вращение плоскости поляризации (эффект фарадея). Оптически неактивные вещества приобретают способность вращать плоскость поляризации под действием магнитного поля. Это явление было обнаружено Фарадеем и поэтому называется иногда эффектом Фарадея. Оно наблюдается только при распространении света вдоль направления намагниченности. Поэтому для наблюдения эффекта Фарадея в полюсных наконечниках электромагнита просверливают отверстия, через которые пропускается световой луч. Исследуемое вещество помещается между полюсами электромагнита или кювету с исследуемым веществом помещают в соленоид. Угол поворота плоскости поляризации ф пропорционален пути l, проходимому светом в веществе и намагниченности вещества. Намагниченность в свою очередь пропорциональна напряженности магнитного поля Н. Поэтому можно написать:
j = VlH. (6)
Коэффициент V называется постоянной Верде или удельным магнитным вращением. Постоянная V, каки постоянная вращения a, зависит от длины волны. Направление вращения определяется направлением магнитного поля. От направления луча знак вращения не зависит. Поэтому если, отразив луч зеркалом, заставить его пройти через намагниченное вещество еще раз в обратном направлении, поворот плоскости поляризации удвоится. Магнитное вращение плоскости поляризации обусловлено возникающей под действием магнитного поля прецессией электронных орбит. Оптически активные вещества под действием магнитного поля приобретают дополнительную способность вращать плоскость поляризации, которая складывается с их естественной способностью. Лекция 6
КВАНТОВАЯ ОПТИКА Тепловое излучение
Как уже отмечалось, излучение телами электромагнитных волн (в частности света) может осуществляться за счет различных видов энергии. Наиболее универсальным является тепловое излучение, которое происходит при любой температуре за счет внутренней энергии тел. Тепловое излучение является равновесным, т. е. если тело при некоторой температуре поместить в идеально отражающую оболочку (рис. 1), количество излученной им энергии будет равно количеству энергии поглощенной.
Интенсивность теплового излучения принято характеризовать энергетической светимостью R – величиной потока энергии (в ваттах), испускаемой единицей поверхности во всех направлениях. Эта величина является функцией температуры и, кроме того, зависит от частоты w. Для интенсивности теплового излучения в диапазоне частот dw можно записать
dRw = rw dw. (1)
Величина rw в (1) называется испускательной способностью тела и также является функцией частоты и температуры. Зная испускательную способность rw, можно вычислить энергетическую светимость:
µ R = òdRwT = òrwTdw. (2)
Излучение можно характеризовать вместо частоты w длиной волны l. Участку спектра dwбудет соответствовать интервал длин волн dl.Определяющие один и тот не участок величины dwи dl связаны простым соотношением, вытекающим из формулы: l = с/v = 2pc/w (частота v и угловая частота w связаны соотношением w = 2pv). Дифференцирование этой формулы дает:
Знак минус в этом выражении указывает на то, что с возрастанием одной из величин, поэтому в дальнейшем мы его не будем писать. Доля энергетической светимости, приходящаяся на интервал dl, может быть по аналогии с (1) представлена в виде:
dRl = rl dl. (4)
Если интервалы dw и dl,входящие в выражения (1) и (4), связаны соотношением (3), т. е. относятся к одному и тому же участку спектра, то величины dRwи dRlбудут совпадать: rwdw = rl dl. Заменив в правой части dl с соответствии с (3), получим:
откуда
При попадании на элементарную площадку тела определенного потока энергии dФw, обусловленного электромагнитными волнами в интервале частот dw, часть его dФ¢w будет поглощена. Величина
aТ,w = dФ¢w/dФw (6)
называется поглощательной способностью тела, aТ,w = a(Т,w). Очевидно, что a (Т, w) не может быть больше 1. Для тела, полностью поглощающего падающее на него излучение, aч = 1 и такое тело называют абсолютно черным или черным. Тела с aТ,w = a(Т) = const < 1 называют серыми. Очевидно, что между испускательной rlТ и поглощательной alT способностями любого типа имеется определённая связь. Действительно, пусть имеется замкнутая оболочка при температуре Т и внутри нее тела обмениваются энергией между собой и оболочкой путём излучения и поглощения. Через некоторое время наступит тепловое равновесие. В таком состоянии, тело с большей rl теряет в единицу времени с единицы поверхности больше энергии, чем тело, обладающее меньшей rl. Т.к. Т = const, то и поглощательная способность его должна быть больше, т.е. должно выполняться условие: (rw,Т/аw,Т)1 = (rw,Т/аw,Т)1 = (rw,Т/аw,Т)1 = … , где индексы соответствуют разным телам.
Кирхгоф установил, что для любых тел справедливо соотношение:
rw,Т/aw,Т = f(w,Т) = rч. (7)
Или отношение испускательной и поглощательной способностей не зависит от природы тел и является универсальной функцией частоты (длины волны) и температуры. Но поскольку для абсолютно черного тела aч = 1, то эта функция равна его испускательной способности rч и характеризует полную плотность излученной энергии при тепловом равновесии. Абсолютно черных тел в природе не существует. Хорошей моделью черного тела является замкнутая полость, имеющая маленькое Результаты экспериментов, полученные с такой моделью, приведены на рис. 3. Разные кривые относятся к различным значениям температуры Табсолютно черного тела. Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре. Кривые спектрального распределения излучения абсолютно черного тела для более низких температур целиком лежат внутри кривых, соответствующих более высоким температурам. Из рисунка видно, что энергетическая светимость сильно возрастает с температурой, а максимум испускательной способности сдвигается в сторону более коротких волн. На рис. 3 приведена не кривая f(w,Т), а кривая j(l,Т), поскольку в экспериментальных работах удобнее измерять (изменять) длину волны, а не частоту. Обе функции связаны друг с другом формулой, аналогичной (5, 5¢):
Согласно (8), для того, чтобы по известной функции f(w,Т) найти функцию j(l,Т) нужно заменить в функции f(w,Т) частоту w на (2pс/l) и полученное выражение умножить на (2pс/l2):
Формулы Рэлея-Джинса и Планка
Рэлей и Джинс сделали попытку определить функцию f(w,Т), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половникам kT – одна половинка на электрическую, вторая – на магнитную энергию волны Рассмотрим излучение, находящееся в равновесии с веществом. Для этого представим себе эвакуированную полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью u = u(Т). Спектральное распределение этой энергии можно охарактеризовать функцией u(w, Т), определяемой условием: duw = u(w, Т)dw, где duw, – доля плотности энергии, приходящаяся на интервал частот dw. Полная плотность энергии может быть представлена в виде:
µ u(T) = òu(w,T)dw. (10)
Равновесная плотность энергии излучения u(Т) зависит только от температуры и не зависит от свойств стенок полости. Это следует из термодинамических соображений. Равновесная плотность излучения u связана с энергетической светимостью абсолютно черного тела R соотношением
R = cu/4 или f(w,T) = cu(w,T)/4. (11)
График, построенный в соответствии с формулой
полученной Рэлеем и Джинсом приведен на рис. 4 (пунктирная линия).
Вывод формулы Рэлея – Джинса с классической точки зрения является безупречным. Поэтому расхождение этой формулы с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической статистической физики и электродинамики. Формулу, соответствующую опытным данным
получил Планк, но для этого он отказался от классических представлений, и предположил, что электромагнитное излучение происходит в виде отдельных порций (квантов), величина которых пропорциональна частоте излучения:
e =
Коэффициент пропорциональности в формуле (14) Формула Планка (13) успешно объяснила полученный ранее из термодинамических соображений закон Стефана-Больцмана, который установил связь между энергетической светимостью абсолютно черного тела Rч и его температурой:
Rч = sТ4, (6)
где s – постоянная Стефана-Больцмана, равная 5,7 10-8 Вт/(м2 К4). Преобразования в соответствии с (9) для j(l,Т) дают:
Из формулы Планка для j(l,Т), после приравнивания к нулю ее производной по температуре, следует установленный ранее экспериментально закон смещения Вина.
Тlм = b, (8)
где lм – длина волны, соответствующая максимуму на кривой (рис. 3, 4), а b – постоянная, равная 2, 9 10-3 м К. Кривые равновесной плотности излучения для разных температур были приведены ранее на рис. 3. Как видно из рисунка площадь под кривой с ростом температуры увеличивается в соответствии с законом (6), а максимум смещается в область более коротких волн в соответствии с законом (7).
Лекция 6 Фотоэффект
Основные особенности явления фотоэффекта были исследованы А.Г.Столетовым. На рис. 1 схематически изображена установка для изучения фотоэффекта. Два металлических электрода, к которым может подаваться напряжение различной полярности, разделены вакуумным промежутком. Величину напряжения можно менять потенциометром. Поверхность одного из электродов облучается монохроматическим излучением. В результате фотоэффекта с поверхности в вакуумном промежутке появляются свободные электроны, и возникает электрический ток, измеряемый чувствительным амперметром. С точки зрения классической теории сам факт образования фотоэлектронов выглядит совершенно естественным. Электрическое поле волны раскачивает электроны, находящиеся внутри твердого тела. В результате их кинетическая энергия возрастает. Если кинетическая энергия превысит работу выхода, электрон с некоторой вероятностью может вылететь с поверхности твердого тела.
Рис. 1. Рис. 2.
Остановимся на результатах опытов, и обсудим, что из них можно, а что нельзя понять в рамках классических представлений. На рис. 2 приведена полученная в эксперименте зависимость фототока от интенсивности излучения. Эта зависимость оказалась прямо пропорциональной, что естественно с классической точки зрения: с увеличением интенсивности излучения растет энергия, поглощаемая электронами в приповерхностном слое металла, а, следовательно, увеличивается вероятность их вылета, т.е. величина фототока. Обсудим теперь зависимость фототока (при некоторой постоянной интенсивности) от величины приложенного между электродами напряжения (рис. 3). Это напряжение может как ускорять электроны, попавшие в вакуумный промежуток, так и тормозить их, возвращая обратно на электрод, препятствуя их вылету. Если напряжение ускоряет электроны, они приобретают дополнительную скорость, направленную к противоположному электроду. В результате величина фототока в цепи растет, пока не достигнет некоторого максимального значения Iнас, соответствующего тому, что все электроны, вылетевшие с поверхности, достигли противоположного электрода. Дальнейшее увеличение напряжения уже не приводит к увеличению фототока. В системе наблюдается насыщение. Величина тока насыщения, однако, линейно зависит от интенсивности излучения. Чем больше интенсивность, тем больше электронов покидает поверхность металла, тем больше ток насыщения.
Рис. 3. Рис. 4.
Другая ситуация возникает, когда полярность поданного напряжения изменена и электроны попадают в тормозящее поле, препятствующее их вылету. В этом случае фототок уменьшается и при некотором напряжении обращается в нуль, что соответствует случаю, когда ни один из электронов не смог достичь поверхности противоположного электрода. Это понятно: существует некоторое значение максимальной кинетической энергии фотоэлектронов. Поэтому фототок должен прекратиться, когда запирающее напряжение Uудовлетворяет условию: eU ≥ E, где E– максимальная кинетическая энергия фотоэлектронов. Непонятно другое: казалось бы, чем больше интенсивность излучения, тем большую кинетическую энергию могут набирать электроны. Действительно, с увеличением интенсивности воздействующего излучения энергия вылетающих с поверхности электронов должна возрастать, следовательно, величина запирающего напряжения увеличиваться. Эксперимент показывает обратное: запирающее напряжение UЗ, а, значит, и максимальная кинетическая энергия фотоэлектронов не зависят от интенсивности излучения. Рассмотрим еще зависимость величины запирающего напряжения от частоты излучения (полученную при постоянной интенсивности излучения). Соответствующая зависимость приведена на рис. 4. Как видно, с увеличением частоты излучения величина запирающего напряжения линейно растет, что свидетельствует о возрастании с частотой энергии фотоэлектронов. Самое интересное, что существует некоторое минимальное значение частоты излучения ωмин (т.н. красная граница фотоэффекта) при которой может наблюдаться фотоэффект. Для значений частот ω < ωмин фотоэффект невозможен. С точки зрения классической физики существование красной границы объяснить нельзя. Выход из создавшейся ситуации был предложен А.Эйнштейном. Развивая идеи Планка, Эйнштейн высказал предположение, что свет представляет собой поток частиц – квантов света, фотонов, несущих энергию e = Действительно, уравнение Эйнштейна для кинетической энергии электронов, вырываемых из атомов (с поверхности твердого тела) полем электромагнитной волны имеет вид:
где A– работа выхода (потенциал ионизации атома для атомного фотоэффекта). В случае hω < Aэнергии кванта недостаточно для удаления электрона с поверхности и фотоэффект невозможен. Из (1) можно определить запирающее напряжение: UЗ = Однако оказалось, что очень высоких интенсивностях излучения (например, сфокусированное лазерное излучение) наряду с процессами поглощения одного кванта света (однофотонный процесс) существенными оказываются также процессы многофотонного поглощения, т.е. процессы в которых происходит одновременное поглощение сразу нескольких фотонов. Применительно к процессу ионизации это означает исчезновение красной границы фотоэффекта: если энергия кванта недостаточна для вырывания электрона из атома, в сильном поле излучения ионизация может произойти в результате поглощения сразу двух фотонов (двухквантовый фотоэффект), а в общем случае – Nфотонов (N-квантовый фотоэффект). Потенциалы ионизации большинства атомов составляют 10-15 эВ, энергия квантов излучения видимого диапазона частот ~2 эВ. Поэтому ионизация атомов оптическим излучением возможна лишь в результате многофотонного поглощения. С учетом сказанного уравнение Эйнштейна можно обобщить на случай многоквантового фотоэффекта
(mV2)/2 = N
где N – число поглощенных фотонов. Экспериментально многоквантовый атомный фотоэффект был обнаружен в 1964 году.
Поиск по сайту: |


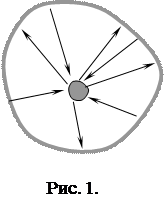
 Рис. 3.
Рис. 3.
 (3)
(3)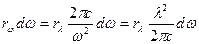 , (5)
, (5) (5¢)
(5¢) . (8)
. (8) и обратно:
и обратно: 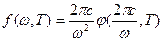 . (9)
. (9) или
или 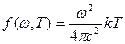 (12)
(12) Однако данная формула – Рэлея-Джинса – удовлетворительно согласу-ется с экспериментом (сплошная кривая на рис. 3) только при больших длинах волн и резко расходится с экспериментом для малых длин волн. Интегрирование (12) по всем динам волн дает для равновесной плотности излучения бесконечно большое значение. Этот результат, получивший название ультрафиолетовой ката-строфы, противоречит опыту.
Однако данная формула – Рэлея-Джинса – удовлетворительно согласу-ется с экспериментом (сплошная кривая на рис. 3) только при больших длинах волн и резко расходится с экспериментом для малых длин волн. Интегрирование (12) по всем динам волн дает для равновесной плотности излучения бесконечно большое значение. Этот результат, получивший название ультрафиолетовой ката-строфы, противоречит опыту.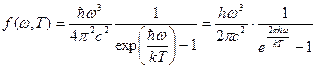 (13)
(13)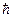 w. (14)
w. (14) . (7)
. (7)

