 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Основной задачей механики является определение положения тела в пространстве и во
Основной задачей механики является определение положения тела в пространстве и во времени. Решению этой задачи способствует ряд физических законов, одним из которых является основной закон динамики вращательного движения абсолютно твердого тела. Абсолютно твердым телом называется тело, деформациями (изменением формы и размеров) которого в условиях данной задачи можно пренебречь. В большинстве случаев реальные тела можно с достаточной для практики точностью считать абсолютно твердыми. В дальнейшем мы их будем называть просто твердыми телами. Основной закон динамики (II закон Ньютона) для вращательного движения твердого тела: в инерциальной системе отсчета угловое ускорение
где Моментом силы относительно неподвижной оси называется физическая величина, равная векторному произведению радиуса-вектора
где
где
Единица измерения момента силы в СИ:
Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведения масс
В случае непрерывного распределения масс эта сумма сводится к интегралу:
где
Единица измерения момента инерции в СИ:
Момент инерции легко рассчитать только в случае тела однородного по плотности и симметричного относительно оси, проходящей через центр масс (воображаемая точка, в которой можно считать сосредоточенной всю массу системы, называемая также центром инерции). Момент инерции тела относительно произвольной оси можно вычислить, используя теорему Штейнера: момент инерции тела
Момент инерции тел неправильной геометрической формы проще определить экспериментально, чем рассчитать. Обоснование метода Получим рабочие формулы для проверки основного закона динамики вращательного движения твердого тела. Модуль углового ускорения маятника связан с модулем линейного ускорения точек на ободе шкива радиуса
Найдём суммарный момент сил, действующих на маятник. К нему приложены сила тяжести и сила натяжения нити. Чтобы упростить задачу, маятник устанавливают в безразличное равновесие, тогда центр тяжести будет лежать на оси маятника и момент силы тяжести будет равен нулю.
Считая нить и блок невесомыми и пренебрегая силами трения в блоке, силу натяжения можно считать одинаковой по всей длине нити. Найдем эту силу. На платформу массы
Проецируя это уравнение на ось Так как Таким образом, момент силы натяжения, то есть суммарный момент сил, действующих на маятник:
Получим выражение для момента инерции маятника. Пусть
Исследование зависимости Описание установки Маятник Обербека, применяемый в данной работе, схематически изображен на рисунке 3.
Все части прибора укреплены на вертикальной колонне 1, установленной на основании 2 с регулируемыми ножками 3 для горизонтальной установки прибора. Основной частью прибора является втулка 4 с четырьмя взаимно перпендикулярными стержнями 5. Ось втулки находится в подшипнике. На ее задний, выступающий из подшипника конец, насажены два легких шкива 6 радиусами На один из шкивов 6 наматывается тонкая нить, переброшенная через легкий блок 8. К свободному концу нити прикреплена платформа 9 массой Автоматический запуск установки, измерение времени падения платформы с гирьками и торможение маятника осуществляются электронной схемой прибора. Она состоит из двух фотоэлектрических датчиков 12, электросекундомера 13 и электромагнита торможения 14 с фрикционным диском 15 (расположен соосно со шкивами 6). При нажатии кнопки «пуск» отключается электромагнит торможения, а при прерывании светового потока в верхнем датчике падающей платформой, включается секундомер. Как только нижний край платформы прервет световой поток в нижнем датчике, одновременно выключается секундомер, и включается электромагнит торможения. Уравнение (1) связывает три физические величины. Опыт же позволяет установить функциональную зависимость каких-либо двух величин – либо Погрешности проведенных измерений можно рассчитать по формулам:
Поиск по сайту: |
 , приобретаемое телом, вращающимся относительно неподвижной оси, прямо пропорционально суммарному моменту
, приобретаемое телом, вращающимся относительно неподвижной оси, прямо пропорционально суммарному моменту  внешних сил, действующих на тело, и обратно пропорционально моменту инерции
внешних сил, действующих на тело, и обратно пропорционально моменту инерции  относительно данной оси:
относительно данной оси: , (1)
, (1) – сумма моментов всех приложенных к телу внешних сил относительно оси вращения.
– сумма моментов всех приложенных к телу внешних сил относительно оси вращения. , проведенного от оси в точку приложения силы, на силу
, проведенного от оси в точку приложения силы, на силу 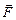 :
: ,
, Модуль момента силы:
Модуль момента силы: ,
, – угол между
– угол между 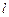 – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
– плечо силы (кратчайшее расстояние между линией действия силы и осью вращения). (ньютон-метр).
(ньютон-метр). материальных точек системы на квадраты их расстояний до рассматриваемой оси:
материальных точек системы на квадраты их расстояний до рассматриваемой оси: .
.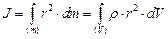 ,
, – плотность тела;
– плотность тела; – объем тела;
– объем тела; – масса тела;
– масса тела;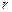 – расстояние от оси вращения.
– расстояние от оси вращения. (килограмм-квадратный метр).
(килограмм-квадратный метр). относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела 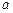 :
: .
. соотношением
соотношением  . Так как нить нерастяжима, то ускорение
. Так как нить нерастяжима, то ускорение  , где
, где 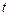 – время движения, получаем:
– время движения, получаем: . (2)
. (2) Таким образом, суммарный момент сил, действующих на маятник, будет определяться только моментом силы натяжения нити.
Таким образом, суммарный момент сил, действующих на маятник, будет определяться только моментом силы натяжения нити. и сила тяжести
и сила тяжести  (рис. 2). Согласно второму закону Ньютона векторная сумма этих сил равна произведению массы платформы на её линейное ускорение:
(рис. 2). Согласно второму закону Ньютона векторная сумма этих сил равна произведению массы платформы на её линейное ускорение: .
. , получаем
, получаем  , т. е.
, т. е.  .
. , получаем
, получаем  .
. . (3)
. (3) – момент инерции одного груза массы
– момент инерции одного груза массы  относительно оси, проходящей через его центр масс. Согласно теореме Штейнера момент инерции этого груза относительно оси вращения маятника будет
относительно оси, проходящей через его центр масс. Согласно теореме Штейнера момент инерции этого груза относительно оси вращения маятника будет 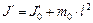 , где
, где  . (4)
. (4) при
при  и
и  , при
, при  позволяет сделать вывод о справедливости основного закона динамики вращательного движения.
позволяет сделать вывод о справедливости основного закона динамики вращательного движения.
 и
и  . По стержням могут перемещаться и закрепляться одинаковые грузы 7 массой
. По стержням могут перемещаться и закрепляться одинаковые грузы 7 массой 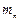 , на которой размещаются гирьки 10 массой
, на которой размещаются гирьки 10 массой  . С целью отсчета пути, проходимого платформой, на колонне 1 нанесена миллиметровая шкала 11. Момент силы, вызывающий вращение маятника, можно менять, помещая на платформе различное число гирек, либо изменяя плечо силы, навивая нить на шкивы разного радиуса.
. С целью отсчета пути, проходимого платформой, на колонне 1 нанесена миллиметровая шкала 11. Момент силы, вызывающий вращение маятника, можно менять, помещая на платформе различное число гирек, либо изменяя плечо силы, навивая нить на шкивы разного радиуса.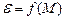 при
при  при
при  , (5)
, (5) , (6)
, (6) . (7)
. (7)