 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Энергией называется скалярная физическая величина, являющаяся единой мерой
Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например, механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и другие. Механическая энергия Кинетическая энергия определяется массами и скоростями движущихся тел (энергия движения). При поступательном движении она определяется следующим выражением:
где
При вращательном движении кинетическую энергию определяют по формуле:
где
Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведения элементарных масс на квадраты их расстояний до рассматриваемой оси:
В случае непрерывного распределения масс эта сумма сводится к интегралу:
где
Для некоторых однородных тел правильной геометрической формы эти интегралы посчитаны и приведены в таблице (прил. 5). Единица измерения момента инерции в СИ:
Если тело участвует в нескольких видах движения, то кинетическая энергия суммируется. Потенциальная энергия зависит от взаимного расположения взаимодействующих друг с другом тел (энергия положения). Вид выражения, по которому рассчитывается потенциальная энергия, зависит от вида рассматриваемого взаимодействия. Для тел, находящихся в однородном гравитационном поле Земли, потенциальная энергия определяется выражением:
где
Вследствие произвольности выбора нулевого уровня потенциальная энергия может принимать отрицательные значения. Как и для любых других видов энергии единицей измерения для вышеназванных в СИ является Энергия подчиняется закону сохранения, который является одним из важнейших законов природы. Закон сохранения энергии: полная механическая энергия тел, движущихся в поле консервативных сил, остается неизменной с течением времени. Математически это можно записать в виде:
Консервативными называются силы, работа которых не зависит от формы траектории движения. При наличии неконсервативных (диссипативных) сил, например, сил трения, полная механическая энергия тела не остается постоянной (часть механической энергии переходит во внутреннюю). Обоснование метода
Проверить закон сохранения полной механической энергии можно при помощи маятника Максвелла. Он представляет собой диск, закреплённый на оси и подвешенный бифилярно на нити, способный совершать колебания в вертикальной плоскости. Рассмотрим движение маятника подробнее. На движущийся маятник действуют консервативные силы тяжести и упругости, а также неконсервативная сила трения о воздух, которой можно пренебречь в силу её малости. В соответствии с законом сохранения, полная механиче
ская энергия маятника во всех точках траектории должна быть одинаковой. Для решения данной задачи удобнее всего рассматривать верхнее и нижнее положения центра тяжести маятника при его движении. Нижнее положение примем за нулевой уровень. В верхней точке маятник будет обладать потенциальной энергией, определяемой выражением
где
В нижней точке потенциальная энергия маятника равна нулю ( Таким образом, полная механическая энергия в этом положении:
где
Непосредственно измерить линейную и угловую скорости не представляется возможным в данном случае, поэтому определим их через другие величины. Центр масс маятника движется равноускоренно, поэтому его линейная скорость определяется по формуле:
где
Ускорение центра масс можно найти, воспользовавшись формулой для определения пути при равноускоренном движении:
Так как маятник в верхнем положении обладает нулевой начальной скоростью, а при своём движении до нижней точки он проходит путь равный
Угловая скорость связана с линейной скоростью следующим выражением:
где С учетом выражений (2) и (3) полная механическая энергия маятника в нижнем положении будет определяться формулой:
Момент инерции маятника можно найти по формуле:
Значения составляющих момента инерции определяются выражениями:
где
Масса маятника складывается из массы оси, ролика и кольца. Таким образом, сравнение значений, полученных из выражений (1) и (4), позволяет сделать вывод о справедливости закона сохранения энергии.
Описание установки Схема установки представлена на рисунке 2.
В основании (1) с регулируемыми ножками (2) для выравнивания прибора закреплена колонка (3), к которой прикреплен неподвижный верхний кронштейн (4) и подвижный нижний кронштейн (5). На верхнем кронштейне находится электромагнит (6), фотоэлектрический датчик № 1 (7) и вороток (8) для регулирования длины бифилярной подвески маятника. Нижний кронштейн с прикрепленным к нему фотоэлектрическим датчиком № 2 (9), можно перемещать вдоль колонки и фиксировать в произвольном положении. Маятник (10) прибора – это бифилярно подвешенный ролик, закрепленный на оси. Для изменения момента инерции маятника на него накладываются сменные кольца (11). Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется с помощью указателя (12) по миллиметровой шкале (13) на колонке прибора. Управление прибором осуществляется с помощью блока (14).
Поиск по сайту: |
 характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Полная механическая энергия равна сумме кинетической
характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Полная механическая энергия равна сумме кинетической  и потенциальной
и потенциальной  энергий.
энергий. ,
, – масса тела;
– масса тела; – скорость движения тела;
– скорость движения тела; ,
, – момент инерции тела;
– момент инерции тела; – угловая скорость.
– угловая скорость. .
.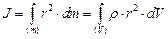 ,
, – плотность тела;
– плотность тела; – объем тела;
– объем тела;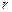 – расстояние от оси вращения.
– расстояние от оси вращения. (килограмм-квадратный метр).
(килограмм-квадратный метр). ,
, – ускорение свободного падения;
– ускорение свободного падения;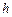 – расстояние от нулевого уровня до центра масс тела (нулевой уровень – начало отсчета – выбирается произвольно).
– расстояние от нулевого уровня до центра масс тела (нулевой уровень – начало отсчета – выбирается произвольно). (джоуль).
(джоуль). .
.
 , и нулевой кинетической энергией, так как его скорость в начальный момент времени равна нулю. Таким образом, полная механическая энергия маятника в этом положении будет определяться только потенциальной энергией:
, и нулевой кинетической энергией, так как его скорость в начальный момент времени равна нулю. Таким образом, полная механическая энергия маятника в этом положении будет определяться только потенциальной энергией: , (1)
, (1) – масса маятника;
– масса маятника;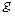 – ускорение свободного падения;
– ускорение свободного падения; ), а кинетическая складывается из энергии поступательного движения центра масс (точка А) и вращательного движения относительно оси вращения, проходящей через центр масс (рис. 1).
), а кинетическая складывается из энергии поступательного движения центра масс (точка А) и вращательного движения относительно оси вращения, проходящей через центр масс (рис. 1). ,
, – момент инерции маятника;
– момент инерции маятника; ,
,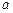 – ускорение, приобретаемое центром масс при движении маятника;
– ускорение, приобретаемое центром масс при движении маятника;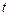 – время его движения;
– время его движения;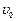 – начальная скорость.
– начальная скорость. .
. . (2)
. (2) , (3)
, (3) – диаметр оси.
– диаметр оси. . (4)
. (4) . (5)
. (5)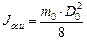 , (6)
, (6) , (7)
, (7)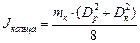 , (8)
, (8) – диаметр ролика;
– диаметр ролика; – внешний диаметр кольца;
– внешний диаметр кольца;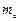 ,
,  ,
,  – массы оси, ролика и кольца соответственно.
– массы оси, ролика и кольца соответственно.