 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Момент инерции – это скалярная физическая величина, являющаяся мерой инертности при
Момент инерции – это скалярная физическая величина, являющаяся мерой инертности при вращательном движении. Инертностью называется способность тел сохранять состояние покоя или равномерного движения. При поступательном движении мерой инертности является масса тела. Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведения масс
В случае непрерывного распределения масс эта сумма сводится к интегралу:
где
Для некоторых однородных тел правильной геометрической формы эти интегралы посчитаны и приведены в таблицах (прил. 5). Единица измерения момента инерции в СИ:
Момент инерции легко рассчитать только в случае тела однородного по плотности и симметричного относительно оси, проходящей через центр инерции (воображаемая точка, в которой можно считать сосредоточенной всю массу системы). Момент инерции тела относительно произвольной оси можно вычислить, используя теорему Штейнера: момент инерции тела
Момент инерции тел неправильной геометрической формы проще определить экспериментально, чем рассчитать.
Обоснование метода Во вращательном движении момент инерции играет такую же роль, какую в поступательном движении играет масса, поэтому знание момента инерции тела имеет большое практическое значение. Определить момент инерции проще всего при помощи крутильного маятника. Если тело с известным моментом инерции
где Если подвесить другое тело с неизвестным моментом инерции
Возведя оба уравнения в квадрат и разделив их друг на друга, будем иметь:
отсюда, выразив
Таким образом, определив периоды колебаний
Описание установки
В основании (1) с регулировочными ножками для выравнивания установки закреплена колонка (2) с кронштейнами (3), (4) и (5). На кронштейнах (3) и (5) установлены зажимы, служащие для закрепления стальной проволоки, на которой подвешена рамка (6). К кронштейну (4) крепится стальная плита (7), служащая основанием фотоэлектрическому датчику (8), электромагниту (9) и шкале (10). Положение электромагнита относительно фотодатчика, которое можно менять, отмечают по шкале, с помощью прикрепленной к нему стрелки. Конструкция рамки позволяет закреплять грузики (11), значительно отличающиеся друг от друга по внешним размерам. Грузики крепятся при помощи подвижной балки, которая перемещается по направляющим и закрепляется путем затягивания гаек на зажимных втулках. Управление установкой осуществляется с помощью блока (12), укрепленного на основании.
Поиск по сайту: |
 материальных точек системы на квадраты их расстояний до рассматриваемой оси:
материальных точек системы на квадраты их расстояний до рассматриваемой оси: .
.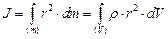 ,
, – плотность тела;
– плотность тела; – объем тела;
– объем тела;  – масса тела;
– масса тела;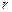 – расстояние от оси вращения.
– расстояние от оси вращения. (килограмм-квадратный метр).
(килограмм-квадратный метр). относительно любой произвольной оси равен сумме момента инерции
относительно любой произвольной оси равен сумме момента инерции  относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела 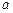 :
: .
. при малых углах закручивания определяется по формуле:
при малых углах закручивания определяется по формуле: , (1)
, (1) – модуль кручения, то есть крутящий момент, возникающий при повороте маятника на угол, равный одной угловой единице (радиану).
– модуль кручения, то есть крутящий момент, возникающий при повороте маятника на угол, равный одной угловой единице (радиану). ), однако модуль кручения при этом останется неизменным, как и вид уравнения, описывающего колебания:
), однако модуль кручения при этом останется неизменным, как и вид уравнения, описывающего колебания: . (2)
. (2) , (3)
, (3) . (4)
. (4) , а также зная
, а также зная 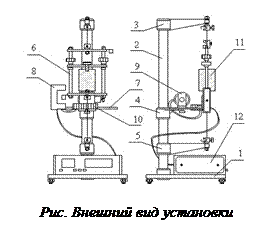 Общий вид установки для определения момента инерции тела представлен на рисунке.
Общий вид установки для определения момента инерции тела представлен на рисунке.