 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Вязкость (внутреннее трение) – это свойство реальных жидкостей оказывать
Вязкость (внутреннее трение) – это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила. Как показал И. Ньютон, сила трения между двумя слоями жидкости площадью
где
Градиент функции – это векторная величина, представляющая собой изменение значения функции на единицу длины в направлении ее наибольшего возрастания). Следовательно, градиент скорости направлен перпендикулярно скорости течения в сторону ее возрастания (рис. 1). Физический смысл: коэффициент вязкости показывает, чему равна сила внутреннего трения, действующая на единицу площади поверхности соприкасающихся слоев при единичном градиенте скорости. Единица измерения вязкости в СИ: Существуют два различных вида течения вязких жидкостей – ламинарное и турбулентное. Течение жидкости, при котором ее соприкасающиеся слои движутся без перемешивания, называется ламинарным. При перемешивании слоев жидкости течение называется турбулентным (скорость частиц в каждой точке потока меняется как по величине, так и по направлению). Английский ученый О. Рейнольдс установил, что характер течения зависит от безразмерной величины, называемой числом Рейнольдса:
где
При малых значениях числа Рейнольдса ( Вязкость является физико-химической константой жидкости только в условиях ламинарного течения. Прибор для измерения вязкости называется вискозиметром. Обоснование метода
В данной работе определение динамической вязкости (коэффициента внутреннего трения) жидкости производится по методу Стокса.
Пусть некоторое тело шарообразной формы и малых размеров движется в вязкой жидкости вертикально вниз (рис. 2). При этом на него будут действовать три силы: сила тяжести
Зная направление действия сил, мы можем переписать уравнение (1) в скалярном виде. В проекциях на ось Ох получим:
В наших опытах тело небольших размеров имеет форму шара. Поэтому, зная выражение для силы Стокса, действующей на шар
где
Таким образом:
В уравнении (4) удобно ввести диаметр шарика
Описание установки
Внешний вид установки представлен на рисунке 3.
На подставке 1 установлен стеклянный цилиндр 2 с касторовым маслом 3. В качестве меток используются два металлических кольца 4, которые могут перемещаться по цилиндру. Для измерения времени используется электронный секундомер ССЭШ 63, включаемый копкой 5 «сеть». При нажатии и удержании кнопки 6 «пуск» происходит измерение времени, которое высвечивается на индикаторах 7, причем первый индикатор показывает секунды, а второй и третий – их десятые и сотые доли соответственно. Обнуление показателей осуществляется кнопкой 8 «сброс».
Поиск по сайту: |

 , отстоящими друг от друга на расстоянии
, отстоящими друг от друга на расстоянии  и отличающимися по скорости течения на величину
и отличающимися по скорости течения на величину 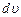 , может быть вычислена из соотношения:
, может быть вычислена из соотношения: ,
, – коэффициент пропорциональности, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью);
– коэффициент пропорциональности, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью); – модуль градиента скорости.
– модуль градиента скорости.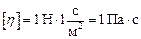 (паскаль-секунда).
(паскаль-секунда). ,
, – кинематическая вязкость;
– кинематическая вязкость; – плотность жидкости;
– плотность жидкости;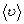 – средняя по сечению трубы скорость жидкости;
– средняя по сечению трубы скорость жидкости; – характерный линейный размер, например, диаметр трубы.
– характерный линейный размер, например, диаметр трубы. ) наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области
) наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области  , а при
, а при  (для гладких труб) течение – турбулентное.
(для гладких труб) течение – турбулентное.
 , сила Архимеда
, сила Архимеда  и сила внутреннего трения жидкости
и сила внутреннего трения жидкости  (сила Стокса), направленная в сторону, противоположную скорости движения тела. При торможении тела о жидкость сила Стокса будет уменьшаться. При этом наступает такой момент, когда движение станет равномерным. Тогда уравнение движения примет следующий вид:
(сила Стокса), направленная в сторону, противоположную скорости движения тела. При торможении тела о жидкость сила Стокса будет уменьшаться. При этом наступает такой момент, когда движение станет равномерным. Тогда уравнение движения примет следующий вид: . (1)
. (1) . (2)
. (2)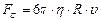 , запишем уравнение движения в следующей форме:
, запишем уравнение движения в следующей форме: , (3)
, (3) – радиус шарика;
– радиус шарика; и
и  – плотности шарика и жидкости;
– плотности шарика и жидкости; – скорость движения шарика.
– скорость движения шарика. . (4)
. (4) и одновременно выразить его скорость через пройденный путь
и одновременно выразить его скорость через пройденный путь 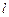 и время
и время 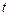 , за которое этот путь пройден. Таким образом, получаем расчетную формулу для определения коэффициента вязкости жидкости методом Стокса:
, за которое этот путь пройден. Таким образом, получаем расчетную формулу для определения коэффициента вязкости жидкости методом Стокса: . (5)
. (5)