 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Основной закон гравитационных взаимодействий установлен в 1687г
Основной закон гравитационных взаимодействий установлен в 1687г. Исааком Ньютоном путем обобщения опытных данных и называется законом всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению масс точек, обратно пропорциональной квадрату расстояния между ними и направленной вдоль прямой, соединяющей эти точки (рис. 1).
где
Закон всемирного тяготения справедлив и для двух однородных шаров, при этом Во всех остальных случаях тела необходимо разбивать на элементарные массы, находить силу тяготения по формуле (1), а затем геометрически складывать (интегрировать), что является часто непростой задачей. В СИ: Гравитационное взаимодействие осуществляется посредством гравитационного поля (поля тяготения). Это поле порождается телами и так же, как вещество и другие физические поля (например, электромагнитное, ядерное) является одной из форм материи. Основное свойство поля тяготения, отличающее его от других физических полей, состоит в том, что на всякое тело массой
Отсюда следует:
Вектор
где
Таким образом, напряженность гравитационного поля – это векторная физическая величина, равная отношению силы тяготения, действующей на тело в данной точке поля, к его массе и имеющая направление силы. Физический смысл напряженности заключается в том, что она показывает, чему равна гравитационная сила, действующая на тело массой Единицей напряженности гравитационного поля в СИ является:
Напряженность
где Потенциал поля тяготения – это скалярная физическая величина, равная отношению потенциальной энергии тела в данной точке поля к его массе. Единицей потенциала гравитационного поля в СИ является:
Физический смысл потенциала поля тяготения заключается в том, что он показывает, чему равна потенциальная энергия тела единичной массы, помещенного в данную точку поля. Напряженность и потенциал связаны между собой соотношением:
где Знак минус в выражении (5) указывает, что вектор напряженности Обоснование метода
Знание напряженности гравитационного поля Земли Наиболее удивительным свойством гравитационных сил, отличающим их от всех других сил в природе, является их способность сообщать всем телам независимо от массы одинаковые ускорения. Поэтому, если пренебречь сопротивлением воздуха и вращением Земли, силу тяготения при свободном падении можно определить по второму закону Ньютона
Таким образом, для нахождения напряженности гравитационного поля Земли достаточно определить ускорение свободного падения. Величина g может быть найдена путем взвешивания или из опытов по свободному падению тел. Более точно ее можно найти, измеряя период колебаний математического или физического маятника.
При малых колебаниях физический маятник совершает гармонические колебания с периодом (временем одного полного колебания), определяемым по формуле:
где
Точка Математический маятник – это идеализированная система, состоящая из материальной точки массой Момент инерции математического маятника определяется выражением:
где Математический маятник можно представить как частный случай физического маятника, предположив, что вся масса сосредоточена в одной точке – центре масс, тогда, подставив выражение (7) в формулу (6), получим выражение для периода малых колебаний математического маятника:
Из сопоставления формул (8) и (6) видно, что приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Однако измерить эту величину на опыте невозможно, поэтому применим способ, исключающий необходимость ее точного измерения. Из рисунка 3 видно, что
Вычитая из первого выражения второе, получим:
Отсюда
Описание установки Схема установки представлена на рисунке 4. Основание (1) оснащено регулируемыми ножками (2), которые позволяют производить выравнивание прибора. В основании закреплена колонка (3), на которой зафиксирован верхний кронштейн (4) и нижний кронштейн (5) с фотоэлектрическим датчиком (6).
Длина маятника регулируется при помощи воротка (8), а её величина определяется с помощью шкалы (9) на колонке (3). Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении. Фотоэлектрический датчик соединен разъемом с привинченным к основанию универсальным миллисекундомером (10).
Поиск по сайту: |
 Величину силы тяготения можно определить по формуле:
Величину силы тяготения можно определить по формуле: , (1)
, (1) – сила притяжения, действующая со стороны массы
– сила притяжения, действующая со стороны массы  на массу
на массу  ;
; – сила притяжения, действующая со стороны массы
– сила притяжения, действующая со стороны массы  – коэффициент пропорциональности, называемый гравитационной постоянной или постоянной тяготения;
– коэффициент пропорциональности, называемый гравитационной постоянной или постоянной тяготения;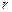 – расстояние между взаимодействующими материальными точками.
– расстояние между взаимодействующими материальными точками. (ньютон-квадратный метр на килограмм в квадрате). Таким образом, два точечных тела массой по
(ньютон-квадратный метр на килограмм в квадрате). Таким образом, два точечных тела массой по 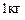 каждое, находящиеся на расстоянии
каждое, находящиеся на расстоянии  друг от друга, притягиваются с силой
друг от друга, притягиваются с силой  . Очень малая величина
. Очень малая величина  .
. , внесенное в это поле, действует сила тяготения
, внесенное в это поле, действует сила тяготения  , пропорциональная массе
, пропорциональная массе  . (2)
. (2) (3)
(3) не зависит от массы тела
не зависит от массы тела  , (4)
, (4) - масса тела, создающего гравитационное поле;
- масса тела, создающего гравитационное поле; (ньютон на килограмм).
(ньютон на килограмм). :
: ,
, – потенциальная энергия тела,
– потенциальная энергия тела,  (джоуль на килограмм).
(джоуль на килограмм). , (5)
, (5) – градиент скаляра
– градиент скаляра  - единичные векторы).
- единичные векторы).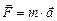 . В то же время, согласно выражению (2),
. В то же время, согласно выражению (2),  . Из равенства величин следует равенство их единиц измерения:
. Из равенства величин следует равенство их единиц измерения:
 Физическим маятником называют любое твердое тело, совершающее колебания под действием сил тяготения относительно неподвижной горизонтальной оси
Физическим маятником называют любое твердое тело, совершающее колебания под действием сил тяготения относительно неподвижной горизонтальной оси  подвеса не проходящей через центр масс
подвеса не проходящей через центр масс 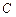 тела (рис.2).
тела (рис.2). (6)
(6) – приведенная длина физического маятника;
– приведенная длина физического маятника; – момент инерции маятника относительно оси, проходящей через точку
– момент инерции маятника относительно оси, проходящей через точку 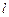 – расстояние от точки подвеса до центра масс маятника.
– расстояние от точки подвеса до центра масс маятника.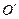 , лежащая на прямой
, лежащая на прямой  на расстоянии
на расстоянии  от точки подвеса маятника
от точки подвеса маятника  , (7)
, (7) . (8)
. (8) Воспользуемся физическим маятником в виде массивного шарика, подвешенного на нити. Приведенной длиной
Воспользуемся физическим маятником в виде массивного шарика, подвешенного на нити. Приведенной длиной  от точки подвеса
от точки подвеса  , где
, где  – некоторое расстояние от центра качания до центра масс. Если измерить периоды колебаний этого маятника при двух значениях приведенной длины и взять их разность, то тем самым исключаются неизвестные значения
– некоторое расстояние от центра качания до центра масс. Если измерить периоды колебаний этого маятника при двух значениях приведенной длины и взять их разность, то тем самым исключаются неизвестные значения 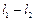 . Для
. Для  и
и 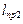 из формулы (6) имеем:
из формулы (6) имеем: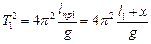 и
и 

 . (9)
. (9) На кронштейне (4) с помощью двух нитей (бифилярно) для создания колебаний в одной плоскости подвешен массивный металлический шарик (7), выполняющий роль физического маятника.
На кронштейне (4) с помощью двух нитей (бифилярно) для создания колебаний в одной плоскости подвешен массивный металлический шарик (7), выполняющий роль физического маятника.