 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Одним из основных законов физики является закон сохранения энергии
Одним из основных законов физики является закон сохранения энергии. В молекулярной физике он формулируется в виде первого начала термодинамики: количество теплоты (Q), сообщенное системе, расходуется на увеличение ее внутренней энергии DU и на совершение системой механической работы (A) против внешних сил:
Внутренней энергией ( Единицей измерения внутренней энергии в СИ является 1 Дж (джоуль). Количество теплоты (Q)–это физическая величина, характеризующая энергию переданную или отданную телу в результате теплообмена. Единица измерения количества теплоты в СИ: 1 Дж (джоуль) Теплообменом называется процесс передачи энергии от одного тела к другому без совершения механической работы. Различают три вида теплообмена: 1. теплопроводность (энергия передаётся от одного тела к другому при непосредственном контакте); 2. конвекция(энергия передаётся от одного тела к другому движущимися потоками жидкости или газа); 3. излучение(энергия передаётся от одного тела к другому в виде электромагнитных волн). Теплоемкостью (С) называется количество теплоты, поглощаемое или отданное телом при изменении его температуры на 1 градус (1°С или 1К):
Единицей измерения теплоемкости в СИ является 1 Дж/К (джоуль на кельвин). Количество теплоты, поглощаемое или отданное телом единичной массы при изменении его температуры на 1 градус (1°Сили 1К) называется удельной теплоемкостью(c) (теплоемкость единицы массы вещества). Удельная теплоемкость определяется соотношением:
Количество теплоты, поглощаемое или отданное одним молем вещества при изменении его температуры на 1 градус (1°С или 1К) называется молярной (мольной) теплоемкостью (Cμ). Молярная теплоемкость связана с удельной соотношением
где m - молярная масса вещества. Количество теплоты, поглощаемое или отданное телом единичного объёма при изменении его температуры на 1 градус (1°С или 1К) называется объёмной теплоемкостью(cоб) (теплоемкость единицы объёма вещества). Объёмная теплоемкость определяется соотношением:
Единицей измерения удельной теплоемкости в СИ является 1 Дж/(кг∙К) (джоуль на килограмм-кельвин), объёмной 1 Дж/(м3∙К) (джоуль на кубический метр-кельвин), молярной 1 Дж/(моль∙К) (джоуль на моль-кельвин). Количество теплоты, поглощенное или отданное телом при изменении его состояния, зависит не только от начальной и конечной температур, но и от способа перехода из одного состояния в другое. Обычно выделяют теплоемкость при постоянном давлении (Ср), если в процессе изменения температуры тела поддерживалось постоянным давление и теплоемкость при постоянном объеме (СV) (не путать с объёмной теплоёмкостью!), если в процессе изменения температуры тела поддерживался постоянный объем. Молярные теплоемкости при постоянном давлении и постоянном объёме определяются следующими соотношениями:
где Связь между этими величинами выражается уравнением Майера: Cpμ = CVμ + R. (7) Оно показывает, что Значение теплоёмкости при постоянном давлении (Cp) сравнительно просто может быть определено из опыта, а теплоёмкость при постоянном объёме (CV) экспериментальному измерению поддается с трудом. Поэтому чаще всего сначала опытным путем находят отношение Cp/CV, а из него рассчитывают значения теплоемкостей при постоянном давлении и объеме (Cp и CV). Отношение теплоемкостей представляет собой характерную для каждого газа величину и входит в уравнение Пуассонадляадиабатического процесса,поэтому получило названиепостоянной адиабаты (γ): g = Cp/CV. (8) Эту постоянную также часто называют показателем адиабаты или коэффициентом Пуассона. Адиабатическим процессом (адиабатным) называется процесс, протекающий без теплообмена с окружающей средой (Q = 0). Уравнение, связывающее термодинамические параметры газа при адиабатическом процессе, называется уравнением адиабаты, или уравнением Пуассона, в честь ученого, который впервые произвел его вывод. Это уравнение можно записать в трех видах: pVg = const; (9) TVg-1 = const; (10) p1-gTg = const. (11) Из формулы (8) с учетом (5) и (6) следует:
Эта формула показывает, что показатель адиабаты, как и теплоемкости, определяется числом степеней свободы молекул идеального газа. Описание установки
Установка (рис.) состоит из стеклянного баллона B, закрытого
пробкой, в которую вмонтированы две трубки. Одна трубка снабжена краном K, с помощью которого баллон может быть соединен либо с насосом N, либо с атмосферой. Вторая трубка соединена с манометром M. Водяной U-образный манометр измеряет разность между давлением в баллоне и атмосферным давлением в миллиметрах водяного столба. Разность между давлением в баллоне и атмосферным измеряется по разности уровней в коленах манометра. Для определения отношения теплоемкостей Cp/CV для воздуха, находящегося в баллоне, с ним проводят последовательность термодинамических процессов, рассматриваемых ниже. Обоснование метода
Обозначим через p0, V0, T0 начальные параметры газа в баллоне. Сначала в баллон накачивается воздух. При этом газ в баллоне сжимается и нагревается. После изохорического остывания до комнатной температуры газ имеет некоторое давление p1 = p0 + h1 и температуру T0. Затем краном соединяют баллон с атмосферой, и газ адиабатически расширяется. При этом происходит охлаждение газа, и его давление падает до величины p0, а температура − до величины T1 < T0. В момент достижения давления p0 кран K перекрывается, и газ изохорически нагревается до комнатной температуры. В конечном состоянии давление газа p2 = p0 + h2, а температура равна T0. В течение всех рассмотренных процессов масса газа в баллоне больше или равна начальной массе газа m0, которую назовем рабочей массой. Накачиваемый и выпускаемый газ служат лишь для сжатия и расширения рабочей массы газа. Уравнение адиабаты (11) для рассматриваемых процессов запишется в виде
Температура T1 после изохорического нагревания становится равной T0, значит, можно записать: p0/T1 = p2/T0. (14) Отсюда T1 = p0T0/p2. (15)
Поиск по сайту: |
 (1)
(1)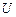 ) тела называется суммарная энергия движения и взаимодействия молекул тела. Для идеального газа полагают, что молекулы между собой не взаимодействуют, следовательно, его внутренняя энергия определяется только кинетической энергией движущихся молекул.
) тела называется суммарная энергия движения и взаимодействия молекул тела. Для идеального газа полагают, что молекулы между собой не взаимодействуют, следовательно, его внутренняя энергия определяется только кинетической энергией движущихся молекул.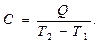 (1)
(1) (2)
(2)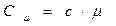 , (3)
, (3) (4)
(4) ; (5)
; (5)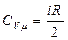 , (6)
, (6)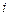 – число степеней свободы (число независимых координат, полностью определяющих положение молекулы в пространстве).
– число степеней свободы (число независимых координат, полностью определяющих положение молекулы в пространстве). всегда больше
всегда больше 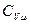 на величину молярной (универсальной) газовой постоянной R (прил. 1).
на величину молярной (универсальной) газовой постоянной R (прил. 1).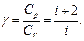 (12)
(12)
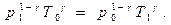 (13)
(13)