ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ В НАУЧНЫХ ПУБЛИКАЦИЯХ

Обоснование объема выборки. Описание участников проведенного исследования должно сопровождаться обоснованием численности выборки, которое является обязательным этапом разработки дизайна проекта. Дело в том, что недостаточный объем выборки увеличивает ошибку выборочных характеристик и может не позволить выявить эффекты там, где они действительно есть, и соответственно, привести к неправильным выводам. С другой стороны слишком большие численности участников приводят к неоправданным финансовым и другим затратам на исследование. Мы уже указывали, что объем выборки зависит от минимального «клинического» эффекта, дисперсии изучаемой величины, мощности используемого критерия и уровня значимости α. Примерная формулировка может звучать таким образом: «Потребовалось 54 пациента в каждой группе, чтобы иметь 85% шанс обнаружить разницу в средних значениях пульса в 10 уд/мин (s=18 уд/мин) при 5% уровне значимости, применяя непараметрический критерий МанаУитни».

Если анализируется несколько признаков (пульс, давление, гемоглобин…) и для каждого из них определяется свой объем выборки, то исследователь может в качестве окончательного выбрать наибольшую из всех рассчитанных численностей, или же задать объем выборки, рассчитанный для главного признака исходя из основной гипотезы.

Оценка закона распределения. Далее желательно указать закон распределения величин, поскольку от этого зависит обоснованность критериев, применяемых для проверки гипотез. Если объем выборки более 30, то можно проверить гипотезу о нормальности распределения одним из известных вам способов, причем проверку необходимо осуществить в каждой группе. Например, «нормальность распределения проверялась по критическим значениям коэффициентов ассиметрии и эксцесса, результаты, приведенные в таблице 89, позволяют принять нулевую гипотезу о нормальном распределении».

Таблица 89. Табличное представление результатов статобработки

п =50

125,04

As=0,424

Ex=0,655

α=0,05

As крит=0,533

Exкрит=0,848

P>0,05

Или: «Нормальность распределения проверялась по критерию хиквадрат, по результатам нулевая гипотеза о нормальности была отвергнута (p=0,03)».

Проверку на нормальность должна пройти каждая из анализируемых признаков.

Если объем выборки мал и не позволяет провести такую проверку, то нужно помнить, что в дальнейшем для сравнительного анализа можно использовать только непараметрические критерии.

Описательная статистика. Как правило, для описания количественных данных используются такие статистические характеристики как средняя, мода, медиана, дисперсия и т.д. При нормальном распределении совокупности применяются среднее значение и среднеквадратичное отклонение (стандартное отклонение) s. Стандартное отклонение дает нам представление, в каких пределах лежат данные генеральной совокупности, так 95,44% всех значений лежит в интервале . Необходимо также указать доверительный интервал для среднего по нему можно оценить, насколько точно оно определено. Для этого предварительно рассчитывается стандартная ошибка среднего m. Если доверительный интервал широкий, то средняя оценена неточно и это может быть связано с недостаточным объемом выборки, или же с большим разбросом данных (дисперсией). Полезно рассчитать коэффициент вариации при V%>33% совокупность считается неоднородной, тогда необходимо проверить, насколько репрезентативна выборка и нет ли аномальных выбросов. Результаты расчетов наглядно могут быть представлены в следующей таблице 90.

Таблица 90. Табличное представление результатов статобработки

	n	(мкмоль/л)	s (мкмоль/л)	95%ДИ (мкмоль/л)	+95%ДИ (мкмоль/л)
1 группа		21,3		21,0	21,6
2 группа		28,5		26,9	30,1

Если распределение случайной величины не соответствует нормальному закону, то в качестве характеристики положения используется медиана, в качестве характеристики разброса – межквартильный размах, а также указываются минимальное и максимальное значения, чтобы определить наличие выбросов. Из приведенной ниже таблицы 91 видно, что в первой группе в середине ранжированного ряда находится величина 4,0 ммоль/л, 50% данных лежит в пределе от 3,3 до 6,0 ммоль/л, максимальное значение 10,5 ммоль/л является явно аномальной. Во второй группе в целом разброс данных больше (∆Q=5,3)и величину 10,5 уже нельзя считать выбросом.

Таблица 91. Основные статистические характеристики

Описание качественных признаков. При анализе качественных номинальных признаков, как правило, подсчитывается доля (частота встречаемости) объектов с заданными свойствами. Доля представляется в виде относительных величин или процентов. Наряду с долей необходимо указывать и абсолютные значения, а для самой доли определить доверительный интервал

Таблица 92. Представление качественных признаков

Иногда, при малых выборках, меньше 10, получается нулевой или 100% эффекты, которые маловероятны. Например, из девяти опрошенных женщин никто не курит – доля равна нулю, ошибка доли также равна нулю. Отсюда можно сделать неправильный вывод, что все женщины некурящие. В этом случае необходимо воспользоваться поправкой на нулевой эффект.

Итоги проверки гипотез. Важное место в любом исследовании занимает процесс сравнения различных совокупностей. Если признаки имеют нормальное распределение, то такое сравнение можно осуществить на основе средних значений с использованием параметрических критериев. Наиболее известным из них является критерий Стъюдента. Нельзя забывать, что его применение требует также и равенства генеральных дисперсий, которое можно проверить по критерию Фишера. При соблюдении всех условий результаты расчетов можно представить в следующей таблице 93.

Таблица 93. Итоги проверки гипотез на основе параметрических критериев

	n		s		95% ДИ	+95% ДИ	tСтъюдента	руровень
1 гр.		119,1	13,9	3,4	6,7	0,1	2,67	<0,05
2 гр.		122,5	16,3

Из таблицы видно, насколько различаются средние значения, по руровню можно оценить статистическую значимость этого различия (при использовании статистических программ лучше указывать конкретное значение достигнутого уровня значимости, например р=0,002). Доверительный интервал показывает, в каких пределах лежит истинная, генеральная разница, а верхний и нижний его пределы позволяют дать «клиническую» оценку этой разнице.

Надо отметить, что в медицинских исследованиях в силу ряда ограничений обычно доступны небольшие выборки, а среди совокупности «больных» нормальное распределение встречается редко. Поэтому приоритет необходимо отдавать непараметрической статистике. При использовании непараметрических критериев результаты описываются на основе медиан и квартилей, например таблица 94.

Таблица 94. Итоги проверки гипотез на основе непараметрических критериев

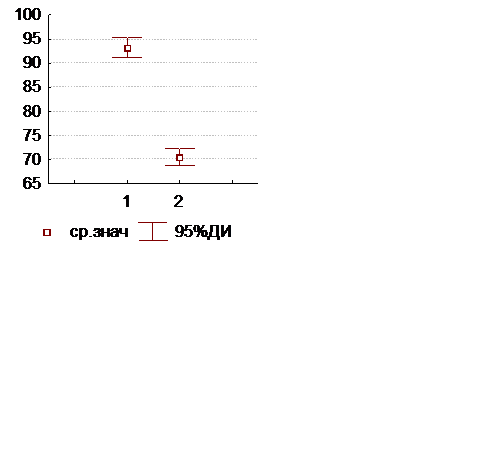
Различия между группами хорошо воспринимаются при графическом представлении данных. Различные возможные варианты показаны на рисунке 40. Не забывайте поместить на графике «легенду» (условные обозначения), так как графики могут нести различную информацию. Если на первом графике представлены средняя, стандартное отклонение, минимальное и максимальное значения, на втором – среднее и доверительный интервал, то на третьем – медиана и квартили.

Рисунок 40. Графическое представление данных

Итоговая информация по результатам сравнения долей должна содержать данные по абсолютным и относительным показателям, а также доверительный интервал для разницы долей.

Таблица 95. Сравнение долей

Доли сравниваются как по критерию Стъюдента, так и по критерию хиквадрат. В случае таблицы 2×2 необходимо учитывать поправку Йетса и упомянуть об этом в тексте. Если таблица содержит ячейку с менее чем 5 случаями, используйте точный критерий Фишера. Силу связи между номинальными признаками оценивают коэффициенты Юла и фиквадрат. Результаты расчетов можно свести в следующую таблицу 96.

Таблица 96. Итоги проверки гипотез на основе таблицы сопряженности

Множественные сравнения. Довольно часто возникает задача сравнения не двух групп, а нескольких – так называемая задача множественных сравнений. Например, различных возрастных, профессиональных, социальных слоев населения, или влияния различных доз препарата, методов диагностики и т.д. В этом случае рекомендуется на начальном этапе провести факторный дисперсионный анализ, который позволяет ответить на вопрос, есть ли хотя бы одно отличие между сравниваемыми группами. Нулевая гипотеза о равенстве всех средних (медиан) проверяется по параметрическому критерию Фишера или непараметрическому аналогу – критерию КрускалаУолиса.

Таблица 97. Итоги факторного дисперсионного анализа

Пакеты прикладных программ по статанализу содержат процедуру Тьюки это процедура множественных попарных сравнений, применяемая в тех случаях, когда дисперсионный анализ указывает на статистически значимую разность между группами. Таким образом, можно выяснить конкретно какие группы отличаются друг от друга.

Как пример, результаты попарных сравнений 6 групп сведены в таблицу 98, в которой указаны средние по группам и значения руровня.

Таблица 98. Множественные попарные сравнения

группа	{1}	{2}	{3}	{4}	{5}	{6}
	=93,2	=80,7	=70,4	=77,3	=80,6	=82,7
{1}		0,000	0,000	0,000	0,000	0,010
{2}	0,000		0,000	0,305	1,000	0,988
{3}	0,000	0,000		0,000	0,000	0,001
{4}	0,000	0,305	0,000		0,151	0,529
{5}	0,000	1,000	0,000	0,151		0,985
{6}	0,010	0,988	0,001	0,529	0,985

Корреляционный анализ. Подсчет коэффициента корреляции также достаточно распространенный метод анализа биомедицинских данных. При его использовании необходимо придерживаться следующих положений:

- предварительно следует построить диаграмму рассеяния, чтобы оценить характер взаимосвязи (линейный или нелинейный)

- коэффициент корреляции Пирсона показывает линейную взаимосвязь между количественными признаками, имеющими нормальное распределение

- если распределение не соответствует нормальному, или признаки ординальные, то применимы коэффициенты Спирмена и Кендалла, оценивающие линейные связи

- для таблиц сопряженности также существуют коэффициенты взаимосвязи (например, коэффициент Юла, фиквадрат)

- следует проверять статистическую значимость коэффициента корреляции и обозначать ее в тексте или таблице

- коэффициент корреляции величина формальная (математическая) и не объясняет причинноследственную связь, интерпретация его – дело специалиста в предметной области

В таблице 99 приведены попарные коэффициенты корреляции и значения руровня. Если принять уровень значимости α=0,05, то r=0,01 и 0,15 статистически незначимы.

Таблица 99. Итоги корреляционного анализа

Регрессионный анализ. Прежде чем приступать к нахождению уравнения регрессии убедитесь, что связь между величинами линейна, для этого подходящим является диаграмма рассеяния. Вычислите коэффициент корреляции, если он меньше 0,7, то нет смысла строить математическую модель, ведь даже при таком значении r она объясняет лишь 50% вариаций. Если уравнение регрессии получено, представьте его графически вместе с наблюдаемыми величинами. Обязательным является оценка статистической значимости коэффициентов уравнения и самой модели, например, таблица 100 является показательной.

Таблица 100. Итоги регрессионного анализа

В случае незначимости коэффициента b₁ (что аналогично незначимости самой регрессии) полученное уравнение не может быть использовано в качестве модели взаимосвязи двух величин.

При прогнозировании по уравнению регрессии рекомендуется проводить прогноз в пределах наблюдаемых значений независимой величины. Если прогноз выходит за эти пределы, вы должны быть уверены, что основная тенденция сохранится в будущем, и при этом прогноз не должен превышать 13 временных интервала.

ЗАКЛЮЧЕНИЕ

В рамках данного пособия затронуты лишь некоторые статистические методы анализа медикобиологической информации. Однако, арсенал их намного более широк, и он не затронут нами, поскольку мы ориентировались на медицинскую аудиторию – студентов, магистрантов, докторантов, научных работников и не решились «грузить» ее сложными математическими выкладками и статистическими интерпретациями.

В последнее время появился целый ряд обзоров, посвященных применению статистики в медицинской науке. Авторы соглашаются с тем, что в абсолютном большинстве исследований используются классические ситуации, когда анализируются один или несколько отдельных признаков, вне их взаимосвязи и взаимовлияния с различной степенью интенсивности. Очень редко встречаются математические модели, описывающие сложные системы, особенно характеризующиеся качественными признаками. Вместе с тем состояние биобъекта не может быть описано с помощью одного или двух показателей изменения или нарушения в одних органах и системах приводят к изменениям и нарушениям в других, и эти взаимосвязи редко являются линейными. В связи с этим особое место в биостатистике занимают многомерные методы анализа. Среди них линейный и нелинейный многомерный регрессионный, логлинейный, дискриминантный, кластерный, факторный анализы и др. Большинство методов реализованы в пакетах статистических программ и пользователи освобождены от необходимости математических вычислений. Основное препятствие их использования – интерпретация результатов, и здесь необходима помощь специалиста, профессионально занимающегося статистикой. Поэтому качественный результат любого научного исследования – это совместный труд медика, владеющего основами биостатистики, и математика, способного понять язык клинициста.

СПИСОК ЛИТЕРАТУРЫ

1. Петри, Авива. Наглядная статистика в медицине: Оқулық/ А. Петри, К. Сэбин; Пер. с англ. М.: ГЭОТАРМЕД, 2009.144с.:ил.

2. Вуколов Э. А. Основы статистического анализа: Практикум по статистическим методам и исследованию операций с использованием пакетов Statistica и EXCEL. М.: ФОРУМ: ИНФРА М, 2004.464с.

3. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: Оқулық / Под ред. В.З. Кучеренко. 2 е изд.,стереотип. М.: ГЭОТАРМедиа, 2005.193 с.

4. Жижин К. С. Медицинская статистика: Оқулық. Ростов н/Д: Феникс, 2007.151с.

5. Гланц Стентон. Медикобиологическая статистика: ағыл. аударған. М.: Практика, 1999.459с.

6. Сергиенко В.И., Бондарева И.Б. Математическая статистика в клинических исследованиях. М.: ГЭОТАРМЕД, 2001.256 с.

7. Юнкеров В.И., Григорьев С.Г. Математикостатистическая обработка данных медицинских исследований. – СПб: ВМедА, 2002. – 266 с.

Приложение 1. Критические значения коэффициента асимметрии As

Приложение 2. Критические точки двустороннего tкритерия Стьюдента

Приложение 3. Критические значения Uкритерия МаннаУитни

α = 0,01. Двусторонний критерий

Приложение 4. Критические значения парного Ткритерия Уилкоксона

Приложение 5. Критические значения χ2

Приложение 6. Критические значения коэффициента корреляции рангов Спирмена

Приложение 7. Критические значения Fкритерия Фишера

для α = 0,05 (обычный шрифт) и α = 0,01 (жирный шрифт)