 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Организация очереди и подсчет средней длины очереди
Очередь, с которой мы встречаемся в быту, предполагает накопитель Н. если в каждый момент поступления заявки знать длину очереди Li, то среднюю длину можно определить по формуле
где n – количество заявок. Пусть в одноканальную систему поступила i-я заявка в момент ti. Пусть L[I - 1] – количество заявок в очереди на момент ti-1. В очереди находятся заявки, которые могут дождаться и пройти обслуживание. Заявка либо обслуживается, либо стоит в очереди, либо получила отказ. Пусть ТН[J] – J = 1, L[I --1], ТН[J] – момент поступления заявки, находящейся в очереди с момента ti-1. Пусть tобсл – момент времени поступления заявки, которая обслуживается в момент ti. Тогда время начала
Если Будем считать основанием для включения в очередь само появление заявки. Сколько заявка находится в очереди? Пока не дойдет до начала обслуживания. В момент начала обслуживания принимается решение об обслуживании или исключении, т. е. в момент Важно, что происходит раньше появление ti+1 или принятие решения Вывод. Точками изменения очереди являются не только ti, но и Может быть случай, когда L[I] = 0 – заявки поступают редко и успевают обслуживаться, очереди нет, или заявки поступают часто, что приводит к образованию очереди. Алгоритм должен все это обрабатывать. Свойства очереди. 1. Каждая заявка попадает сначала в очередь. 2. В очереди могут быть заявки с произвольными номерами (неоднородность по времени обслуживания). 3. Длина очереди изменяется в момент поступления очередной заявки и в момент принятия решения об обслуживании или отказе. Заявки. t[I] – моменты появления заявок
Если
Нужно сформировать объединенный массив Для очереди нужен массив моментов рассмотрения i-й заявки tр[I], i-я заявка рассматривается после (i - 1)-й и в тот момент, когда для нее подойдет момент начала обслуживания, т. е. от ti до tн[I] заявка в очереди.
8. Программная реализация алгоритмов
Поиск по сайту: |
 ,
, обслуживания заявки определяется как
обслуживания заявки определяется как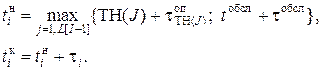
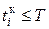 и
и 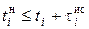 , то заявка попадет в очередь и будет обслужена. При таком подходе мы увидим в очереди лишь те заявки, которые будут обслужены, что не соответствует реальности.
, то заявка попадет в очередь и будет обслужена. При таком подходе мы увидим в очереди лишь те заявки, которые будут обслужены, что не соответствует реальности. , t[I] Î [t0, t0 + T], t[I + 1] > t[I]. По реализации можно сформировать массив tн[I] – моментов начала обслуживания I-й заявки, которая будет обслужена и массив N[I] – номеров заявок, которые будут обслужены.
, t[I] Î [t0, t0 + T], t[I + 1] > t[I]. По реализации можно сформировать массив tн[I] – моментов начала обслуживания I-й заявки, которая будет обслужена и массив N[I] – номеров заявок, которые будут обслужены. .
.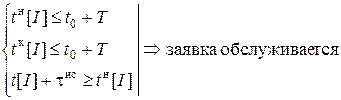 .
. и каждому
и каждому