 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Классификация систем массового обслуживания
По количеству обслуживающих приборов СМО делятся на одноканальные и многоканальные. Многоканальные СМО состоят из нескольких приборов, и каждый них может обслуживать заявку. Также СМО подразделяются на системы без ожидания и с ожиданием. В первых заявка покидает очередь, если к моменту её прихода отсутствует хотя бы один канал, способный немедленно приступить к обслуживанию данной заявки. Вторые, в свою очередь, делятся на системы без ограничения и с ограничениями по длине очереди. Также СМО делятся на системы с приоритетами и без них. В свою очередь системы с приоритетом делятся на СМО с прерыванием и без.
Одноканальная СМО с неограниченной очередью
Рис.4.3 Найдем вероятности pk: Для состояния S0: Для состояния S1n: Вероятность p0 найдем из нормировочного условия
В текущий момент времени в системе может быть 0, 1, 2, ..., k, ... заявок с вероятностями p0, p1 p2,... Математическое ожидание количества заявок:
учитывая, что
Средняя длина очереди равна разности между средним числом заявок в системе и средним числом заявок, находящихся под обслуживанием: Формулы Литтла
Первая формула Литтла позволяет определить время реакции СМО (время пребывания заявки в системе). Пусть X(t) – число заявок, поступивших в СМО до момента времени t, Y(t) – покинувших СМО до t. Обе функции случайны и увеличиваются скачком на единицу в моменты прихода и ухода заявок. Тогда число заявок в системе в момент времени t можно определить как:
Интеграл равен площади ступенчатой фигуры, ограниченной функциями X(t) и Y(t), эта сумма состоит из прямоугольников, ширина которых равна единице, а длина – времени пребывания i-ой заявки в системе. Сумма распространяется на все заявки, поступившие в систему за время T. Правую часть домножим и разделим на l: Совершенно аналогично можно получить среднее время пребывания заявки в очереди:
Поиск по сайту: |

 , отсюда
, отсюда  ;
; , подставляем полученное значение для p1:
, подставляем полученное значение для p1:  . Аналогично,
. Аналогично, 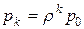 .
. :
: ,
,  – геометрическая прогрессия, при r<1 сходится.
– геометрическая прогрессия, при r<1 сходится.  – вероятность того, что нет заявок.
– вероятность того, что нет заявок. – вероятность того, что прибор занят обслуживанием заявки. r=l/m – мера загрузки одноканальной СМО.
– вероятность того, что прибор занят обслуживанием заявки. r=l/m – мера загрузки одноканальной СМО.
 , получим:
, получим: .
. .
.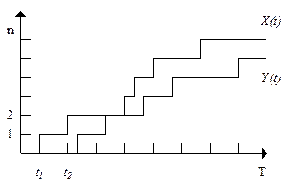 Рис.4.4
Рис.4.4
 . Рассмотрим очень большой промежуток времени T и вычислим среднее число заявок в системе:
. Рассмотрим очень большой промежуток времени T и вычислим среднее число заявок в системе: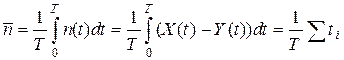 .
. . Tl – среднее количество заявок, пришедших за время T. Поделив сумму всех времен ti на среднее число заявок, получим среднее время пребывания заявки в системе:
. Tl – среднее количество заявок, пришедших за время T. Поделив сумму всех времен ti на среднее число заявок, получим среднее время пребывания заявки в системе: 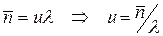 .
. .
.