 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задача о производителе/потребителе
В задаче о производителе/потребителе также присутствует совместно используемый объект, но в этом случае разделяемый объект точно определен и является буфером. Процесс-производитель создает объекты, которые помещаются в буфер. Потребитель ждет, пока объект не будет помещен в буфер, удаляет его оттуда и использует. Такая ситуация может быть промоделирована сетью Петри так, как показано на рис.5.11. Позиция B представляет собой буфер, каждая фишка соответствует элементу данных, который произведен, но еще не использован.
Один из вариантов этой задачи – это задача о нескольких производителях/нескольких потребителях. В этом случае несколько производителей порождают элементы данных, помещаемые в общий буфер, для нескольких потребителей. На рис.5.12 представлено решение этой задачи в виде сети Петри. Эта сеть совпадает с сетью на рис.5.11, за исключением того, что для представления s производителей и t потребителей мы начали выполнение сети с s фишками в начальной позиции процесса-производителя и t фишками в начальной позиции процесса-потребителя. Таким образом мы представляем s производителей и t потребителей, реализуемых реентерабельными совместно используемыми программами. Альтернативой было бы дублирование программного кода для процессов производителя и потребителя, однако результатом этого при том же самом поведении была бы гораздо большая сеть.
В другом варианте задачи о производителе/потребителе используется буфер ограниченного размера. При такой постановке задачи буфер между производителем и потребителем ограничен, т. е. имеет только n ячеек для элементов данных. Следовательно, производитель не может постоянно работать с той скоростью, которая ему нужна, а вынужден ждать, если потребитель работает медленно и буфер заполнен. На рис.5.13 показано решение этой проблемы. Ограниченному буферу сопоставляются две позиции: B представляет количество элементов данных, которые произведены, но еще не использованы (число заполненных ячеек). B' – количество пустых ячеек в буфере. Первоначально B' имеет n фишек, а B фишек не имеет. Если буфер заполнен, то B' фишек не имеет, а B имеет n фишек. Если теперь производитель попытается поместить еще один элемент данных в буфер, то. он будет остановлен, так как в В' нет фишки, делающей этот переход разрешенным.
Химические системы – другой пример систем, которые могут быть промоделированы сетями Петри. Химические уравнения моделируются переходами; вещества, участвующие в реакции, – позициями. Количество фишек в позиции указывает на количество данного вещества в системе. Например, сеть Петри на рис.5.14 представляет два химических уравнения:
Безопасность Одно из важнейших свойств сети Петри, которая должна моделировать реальное устройство, – безопасность. Позиция сети Петри является безопасной, если число фишек в ней никогда не превышает 1. Сеть Петри безопасна, если безопасны все позиции сети. Определение 10. Позиция piÎP сети Петри С= (Р, Т, I, O) с начальной маркировкой m является безопасной, если m'£1 для любой m' Î R(C, m). Сеть Петри безопасна, если безопасна каждая ее позиция. Безопасность – очень важное свойство для устройств аппаратного обеспечения. Если позиция безопасна, то число фишек в ней равно 0 или 1. Следовательно, позицию можно реализовать одним триггером. В первоначальном определении сети Петри были безопасны, поскольку переход не мог быть запущен, если не все из выходных позиций были пусты (а кратные дуги не были разрешены). Это объяснялось интерпретацией позиции как условия. Условие, будучи логическим высказыванием, либо истинно (представляется фишкой в позиции), либо ложно (представляется отсутствием фишки); кратные фишки не имеют никакой интерпретации. Таким образом, если интерпретировать сети как условия и события, маркировка каждой позиции должна быть безопасной. Если позиция не является кратной входной или кратной выходной для перехода, ее можно сделать безопасной. К позиции pi, которую необходимо сделать безопасной, добавляется новая позиция p'i. Переходы, в которых pi используется в качестве входной или выходной, модифицируются следующим образом: Если piÎ I(tj) и pi Ï O(tj), тогда добавить p'i к O(tj). Если pi Î O(tj) и pi Ï I(tj), тогда добавить p'i к I(tj).
Цель введения этой новой позиции p'i – представить условие «pi пуста». Следовательно, pi и p'i дополнительны; pi имеет фишку, только если p'i не имеет фишки и наоборот. Любой переход, удаляющий фишку из pi, должен помещать фишку в p'i, а всякий переход, удаляющий фишку из pi, должен помещать фишку в p'i. Начальная маркировка также должна быть модифицирована для обеспечения того, чтобы точно одна фишка была либо в pi, либо в p'i. (Мы допускаем, что начальная маркировка безопасна.) Заметим, что такая принудительная безопасность возможна только для позиций, которые в начальной маркировке являются безопасными и входная и выходная кратность которых равна 0 или 1 для всех переходов. Позиция, имеющая для некоторого перехода выходную кратность 2, будет получать при его запуске две фишки и, следовательно, не может быть безопасной. Простая сеть Петри на рис.5.15 реобразована в безопасную, как показано на рис.6.16 Ограниченность Безопасность – это частный случай более общего свойства ограниченности. Некоторые соображения относительно реального ограничения на аппаратную, реализацию позиций позволяют прийти к заключению, что безопасность – необязательное требование. Безопасность позволяет реализовать позицию триггером, но в более общем случае можно использовать счетчик. Однако любой аппаратно реализованный счетчик ограничен по максимальному числу, которое он может представить. Позиция является k-безопасной или k-ограниченной, если количество фишек в ней не может превышать целое число k. Определение 11. Позиция pi Î P сети Петри С = (Р, Т, I, O) с начальной маркировкой m является k-беэопасной, если m'(pi) £ k для всех m' Î R(C, m). Иногда нас будет интересовать только то, является число фишек в позиции ограниченным или нет, а не конкретное значение границы. Позиция называется ограниченной, если она k–безопасна для некоторого k; сеть Петри ограниченна, если все ее позиции ограниченны. Ограниченную сеть Петри можно реализовать аппаратно, тогда как сеть Петри с неограниченными позициями в общем cлучае реализовать аппаратно нельзя.
Методы анализа В этом разделе мы представим два основных метода анализа сетей Петри, которые описывают механизмы решения некоторых из уже перечисленных задач. Первый метод анализа, используемый для сетей Петри, – это дерево достижимости, второй метод связан с. матричными уравнениями. Обсудим каждый из них.
Дерево достижимости Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис.5.17. Начальная маркировка ее – (1, 0, 0). В этой начальной маркировке разрешены два перехода: t1 и t2. Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис.5.18). Это (частичное) дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.
Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1, 1, 0) можно снова запустить t1 (получая (1, 2, 0)) и t2 (получая (0, 2, 1)); из (0, 1, 1) можно запустить t3 (получая (0, 0, 1)). Это порождает дерево, изображенное на рис.5.19. Начиная с трех новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево, как показано на рис.5.20.
Рис.5.18 Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешенным, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут. Кроме того, необходимо отметить, что маркировка (0, 1,1), порождаемая запуском t3 в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском t2.
Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порожденной. Однако получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рис.5.21).
Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера. Приведение к конечному представлению осуществляется несколькими способами. Нам необходимо найти те средства, которые ограничивают введение новых маркировок (называемых граничными вершинами) на каждом шаге. Здесь могут помочь пассивные маркировки – маркировки, в которых нет разрешенных переходов. Эти пассивные маркировки называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Такие дублирующие маркировки называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве. В сети Петри на рис.5.16, например, можно запустить переход t1 столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в p2. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа w, который обозначает «бесконечность». Для любого постоянного a определим
Для построения дерева достижимости необходимы только эти операции над w. Теперь можно точно сформулировать действительный алгоритм построения дерева достижимости. Каждая вершина i дерева связывается с расширенной маркировкой m[i]; в расширенной маркировке число фишек в позиции может быть либо неотрицательным целым, либо w. Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые еще не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.
Алгоритм начинает работу с определения начальной маркировки корнем дерева, т. е. граничной вершиной. До тех пор пока имеются граничные вершины, они обрабатываются алгоритмом. Пусть х – граничная вершина, которую необходимо обработать. 1. Если в дереве имеется другая вершина у, не являющаяся граничной, и с ней связана та же маркировка, m[х] = m[y], то вершина х – дублирующая. 2. Если для маркировки m[х] ни один из переходов не разрешен (т. е. d(m[x], tj) не определено для всех tj Î T), то х – терминальная вершина. 3. Для всякого перехода tj Î T, разрешенного в m[х] (т. е. d(m[х], tj) определено), создать новую вершину z дерева достижимости. Маркировка m[z], связанная с этой вершиной, определяется для каждой позиции pi следующим образом: а) Если .m[x]i = w, то m[z]i = w. б) Если на пути от корневой вершины к х существует вершина у с m[y] < d(mlxl, tj) и m[y]i < d(m[x], tj)i, то m[z]i = w. в) В противном случае m[z]i = d(m[х], tj)i. Дуга, помеченная tj, направлена от вершины х к вершине z. Вершина х переопределяется как внутренняя, вершина z становится граничной. Когда все вершины дерева – терминальные, дублирующие или внутренние, алгоритм останавливается. На рис.5.22 представлено дерево достижимости для сети Петри на рис.5.16.
Матричные уравнения Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Альтернативным по отношению к определению сети Петри в виде (Р, Т, I, O) является определение двух матриц D- и D+, представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим D-[j, i] = #(pi, I(tj)), a D+[j, i] = #(pi, O(tj)). D- определяет входы в переходы, D+ – выходы. Матричная форма определения сети Петри (Р, Т, D-, D+) эквивалентна стандартной форме, используемой нами, но позволяет дать определения в терминах векторов и матриц. Пусть е[j] – m-вектор, содержащий нули везде, за исключением j-ой компоненты. Переход tj представляется m-вектором e[j][1]. Теперь переход tj в маркировке m разрешен, если m. ³ е[j], а результат запуска перехода tj в маркировке m. записывается как
где D = D+ – D+ – составная матрица изменений. Тогда для последовательности запусков переходов
Вектор f(s) = e[j1] + е[j2] + ... + e[jk] называется вектором запусков последовательности Для того чтобы показать полезность такого матричного подхода к сетям Петри, рассмотрим, например, задачу сохранения: является ли данная маркированная сеть Петри сохраняющей? Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть w-n´1 – вектор-столбец. Тогда, если m – начальная маркировка, а m' – произвольная достижимая маркировка, необходимо, чтобы
Следовательно, Поскольку это должно быть верно для всех f(s), имеем Развитая матричная теория сетей Петри является инструментом для решения проблемы достижимости. Предположим, что маркировка m' достижима из маркировки m. Тогда существует последовательность (возможно, пустая) запусков переходов s, которая приводит из m к m'. Это означает, что f(s) является неотрицательным целым решением следующего матричного уравнения для х:
Следовательно, если m' достижима из m тогда уравнение (*) имеет решение в неотрицательных целых; если уравнение (*) не имеет решения, тогда m' недостижима из m.
Рассмотрим, например, маркированную сеть Петри на рис.5.23. Матрицы D- и D+ имеют вид:
а матрица D:
В начальной маркировке m = (1, 0, 1, 0) переход t3 разрешен и приводит к маркировке m', где
Последовательность
Для определения того, является ли маркировка (1,8,0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение
которое имеет решение x = (0, 4, 5). Это соответствует последовательности s = t3t2t3t2t3t2t3t2t3. Далее мы можем показать, что маркировка (1,7,0, 1) недостижима из маркировки (1, 0, 1, 0), поскольку матричное уравнение
не имеет решения. Матричный подход к анализу сетей Петри очень перспективен, но имеет и некоторые трудности. Заметим прежде всего, что матрица D сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц D- и D+, но затем взаимно уничтожаются в матрице D = D- – D+. Это отражено в предыдущем примере позицией p1 и переходом t1.
Другая проблема – это отсутствие информации о последовательности в векторе запуска. Рассмотрим сеть Петри на рис.5.24. Предположим, мы хотим определить, является ли маркировка (0, 0, 0, 0, 1) достижимой из (1, 0, 0, 0, 0).
Тогда имеем уравнение
Это уравнение не имеет однозначного решения, но сводится к множеству решений {s½f(s)=(1, x2, x6-1, 2x6, x6-1, x6)}. Оно определяет взаимосвязь между запусками переходов. Если положим x6=1 и x2=1, то f(s)=(1, 1, 0, 2, 0, 1), но этому вектору запуска соответствуют как последовательность t1t2t4t4t6, так и последовательность t1t4t2t4t6. Следовательно, хотя и известно число запусков переходов, порядок их запуска неизвестен.
Еще одна трудность заключается в том, что решение уравнения (*) является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведенную на рис.5.25. Если мы хотим определить, является ли (0, 0, 0, 1) достижимым из (1,0,0,0), необходимо решить уравнение
Это уравнение имеет решение f(s) = (1, 1), соответствующее двум последовательностям: t1t2 и t2t1. Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни t1, ни t2 не разрешены. Таким образом, решения уравнения (*) недостаточно для доказательства достижимости. Возможность недействительных решений уравнения (*) (решений, которые не соответствуют возможным последовательностям переходов) стала причиной только ограниченного исследования матричного представления сетей Петри.
Поиск по сайту: |
 Рис.5.11. Задача о производителе/потреьителе
Рис.5.11. Задача о производителе/потреьителе
 Рис.5.12.
Рис.5.12.
 Рис.5.13.
Рис.5.13.

 Рис.5.14
Рис.5.14

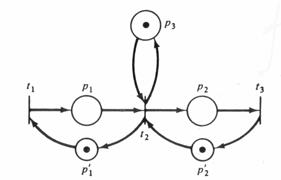 Рис.5.15 Рис.5.16
Рис.5.15 Рис.5.16
 Рис.5.17.
Рис.5.17.

 Рис.5.19.
Рис.5.19.
 Рис.5.21. Простая сеть Петри с бесконечным деревом.
Рис.5.21. Простая сеть Петри с бесконечным деревом.

 Рис.5.22.
Рис.5.22.
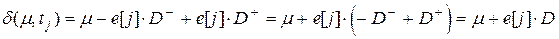 ,
, имеем
имеем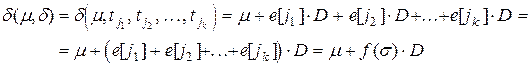
 . i–й элемент вектора f(s), f(s)i – это число запусков перехода ti в последовательности
. i–й элемент вектора f(s), f(s)i – это число запусков перехода ti в последовательности  . Теперь, поскольку m' достижима, существует последовательность запусков переходов s, которая переводит сеть из m в m'. Поэтому
. Теперь, поскольку m' достижима, существует последовательность запусков переходов s, которая переводит сеть из m в m'. Поэтому .
. , поэтому
, поэтому  .
. . Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор w, что
. Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор w, что  . (*)
. (*) Рис.5.23.
Рис.5.23.






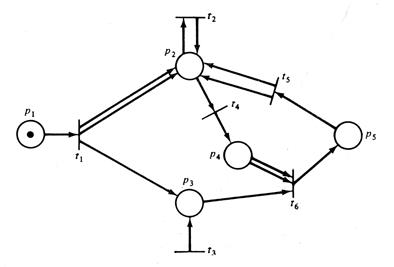 Рис.5.24.
Рис.5.24.

 Рис.5.25.
Рис.5.25.
