 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Многоканальная СМО с неограниченной очередью
Рис.4.5 Найдем вероятности pk: Для состояния S0: Для состояний S1– Sn: Для Sn+1: Для Sn+s-1: Для Sn+s: Из первых n+1 уравнений получаем: Из последнего уравнения выражаем: Продолжая аналогию: Теперь найдем p0, подставив полученные выражения в нормировочное условие ( Показатели эффективности СМО – Вероятность потери требования в СМО. Особенно часто ею пользуются при исследовании военных вопросов. Например, при оценке эффективности противовоздушной обороны объекта она характеризует вероятность прорыва воздушных целей к объекту. Применительно к СМО с потерями она равна вероятности занятости обслуживанием требований всех n приборов системы. Чаще всего эту вероятность обозначают pn или pотк. – Вероятность того, что обслуживанием требований в системе занято k приборов, равна pk. – Среднее число занятых приборов: – Среднее число свободных от обслуживания приборов : – Коэффициент простоя приборов: – Коэффициент занятости оборудования: – Средняя длина очереди: – Среднее число заявок, находящихся в сфере обслуживания: – Вероятность того, что число заявок в очереди, ожидающих начала обслуживания, больше некоторого числа m: Кроме перечисленных критериев при оценке эффективности СМО могут быть использованы стоимостные показатели: qоб – стоимость обслуживания каждого требования в системе; qож – стоимость потерь, связанных с простаиванием заявок в очереди в единицу времени; qу – убытки, связанные с уходом из системы заявки; qk – стоимость эксплуатации каждого прибора в единицу времени; qkпр – стоимость простоя единицы времени k-го прибора системы. При выборе оптимальных параметров СМО по экономическим показателям можно использовать функцию стоимости потерь в системе (для СМО с ожиданием): Для СМО с отказами: Для смешанных: Критерий экономической эффективности СМО:
СМО замкнутого типа
Пример. С1, С2, С3 – станки; НЦ – центральный накопитель; B – манипулятор. Транспортная тележка (манипулятор) транспортирует отработанную деталь от станка к накопителю и укладывает ее там, забирает новую деталь (заготовку), транспортирует ее к станку и устанавливает в рабочую позицию для зажима. Во время всего периода, необходимого для выгрузки–загрузки, станок простаивает. Время Tз смены заготовки и есть время обслуживания. Интенсивность обслуживания станков определяется как Станочная система с однозахватным манипулятором представляет собой СМО с ожиданием с внутренней организацией FIFO: каждая заявка станка на обслуживание удовлетворяется, в случае когда манипулятор занят, заявка становится в очередь и станок ожидает когда манипулятор освободится. Данный процесс марковский, т.е. случайная выдача заявки на обслуживание в определенный момент времени t0 не зависит от предыдущих заявок, т.е. от течения процесса в предшествующий период. Продолжительность исполнения заявки может быть различной и является случайной величиной, не зависящей от числа поданных заявок. Весь процесс не зависит от того, что произошло ранее момента времени t0. В станочной системе число заявок на обслуживание может быть равно 0, 1, 2, ... m, где m – общее число станков. Тогда возможны следующие состояния: S0 – все станки работают, манипулятор стоит. S1 – все станки, кроме одного, работают, манипулятор обслуживает станок, от которого поступила заявка на смену заготовок. S2 – работают m-2 станка, на одном станке идет смена заготовки, другой ожидает. S3 – работают m-2 станка, один станок обслуживается манипулятором, два станка ожидают в очереди. Sm – все станки стоят, один обслуживается манипулятором, остальные ожидают очереди исполнения заказа.
Рис.4.6. Вероятность перехода в состояние Sk из одного из возможных состояний S1, S2, ... Sm зависит от случайного поступления заявок на обслуживание и вычисляется как:
p0 – вероятность того, что все станки работают. Манипулятор работает при состояниях системы от S1 до Sm. Тогда вероятность его загрузки равна: Число станков, находящихся в очереди связано с состояниями S2, – Sm, при этом один станок обслуживается, а (k-1) – ожидают. Тогда, среднее число станков в очереди: Коэффициент простоя одного станка (из-за ожидания при многостаночном обслуживании): Среднее использование одного станка:
Поиск по сайту: |

 ;
;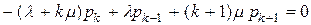 ;
; ; ...
; ... ;
; .
.
 и подставляем в предпоследнее:
и подставляем в предпоследнее:  ,
,  . Тогда
. Тогда  .
. .
. ):
):  . Отсюда
. Отсюда  .
. характеризует степень загрузки обслуживающей системы.
характеризует степень загрузки обслуживающей системы. .
. .
. .
. , pk - вероятность того, что в системе находится k требований.
, pk - вероятность того, что в системе находится k требований. .
. . Этот показатель особенно необходим при оценке возможностей размещения требований при ограниченности времени для ожидания.
. Этот показатель особенно необходим при оценке возможностей размещения требований при ограниченности времени для ожидания.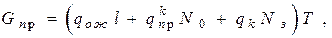 T – интервал времени.
T – интервал времени. .
. .
. , с – экономический эффект, получаемый при обслуживании каждой заявки.
, с – экономический эффект, получаемый при обслуживании каждой заявки.
 ,
,  – среднее время обслуживания станка, которое вычисляется как
– среднее время обслуживания станка, которое вычисляется как  , где n – число заявок. Интенсивность подачи станком заявки на обслуживание определяется как
, где n – число заявок. Интенсивность подачи станком заявки на обслуживание определяется как  (где
(где  – среднеее время обработки детали станком).
– среднеее время обработки детали станком).
 ;
; .
. .
. .
. .
.