Псевдослучайные последовательности.

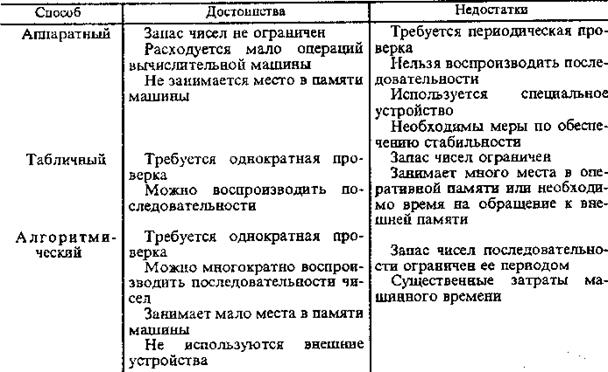
При статистическом моделировании систем одним из основных вопросов является учет стохастических воздействий. Количество случайных чисел, используемых для получения статистически устойчивой оценки характеристики процесса функционирования системы S при реализации моделирующего алгоритма на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно и большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества исходных (базовых) последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования, последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделирования систем.

На практике используются три основных способа генерации случайных- чисел:

1. аппаратный (физический);

2. табличный (файловый);

3. алгоритмический (программный).

Аппаратный способ. При этом способе генерации случайные числа вырабатываются специальной электронной приставкой — генератором (датчиком) случайных чисел,— служащей в качестве одного из внешних устройств ЭВМ. Таким образом, реализация этого способа генерации не требует дополнительных вычислительных операций ЭВМ по выработке случайных чисел, а необходима только операция обращения к внешнему устройству (датчику). В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т. д. Рассмотрим принцип получения случайных чисел от приставки, основанный, например, на эффекте шума в полупроводниковых приборах.

Структурная схема аппаратного генератора случайных чисел приведена на рис. 1.

Рис. 1.

Где ИШ — источник шума; КС— ключевая схема; ФИ — формирователь импульсов; ПС — пересчетная схема, При усилении шумов на выходе ИШ получается напряжение иш(t), которое является случайным процессом, показанным на временной диаграмме рис. 1. Причем отрезок шумовой реализации их (t), сформированный на интервале времени (0, T) с помощью КС, содержит случайное число выбросов. Сравнение напряжения иk (t) с пороговым Un позволяет сформировать на выходе ФИ серию импульсов иф(t). Тогда на выходе ПС может быть получена последовательность случайных чисел Xi(t).

Например, если провести масштабирование и принять длину интервала (0, T) за единицу, то значения интервалов времени , между соседними импульсами иф(t) будут случайными числами хi(0, 1). Возможны и другие схемные решения аппаратных генераторов случайных чисел.

Однако аппаратный способ получения случайных чисел не позволяет гарантировать качество последовательности непосредственно во время моделирования системы S на ЭВМ, а также повторно получать при моделировании одинаковые последовательности чисел.

Табличный способ. Если случайные числа, оформленные в виде таблицы, помещать во внешнюю или оперативную память ЭВМ, предварительно сформировав из них соответствующий файл (массив чисел), то такой способ будет называться табличным. Однако этот способ получения случайных чисел при моделировании систем на ЭВМ обычно рационально использовать при сравнительно небольшом объеме таблицы и соответственно файла чисел, когда для хранения можно применять оперативную память. Хранение файла во внешней памяти при частном обращении в процессе статистического моделирования не рационально, так как вызывает увеличение затрат машинного времени при моделировании системы S из-за необходимости обращения к внешнему накопителю. Возможны промежуточные способы организации файла, когда он переписывается в оперативную память периодически по частям. Это уменьшает время на обращение к внешней памяти, но сокращает объем оперативной памяти, который можно использовать для моделирования процесса функционирования системы S.

Алгоритмический способ. Способ получения последовательностей случайных чисел основан на формировании случайных чисел в ЭВМ с помощью специальных алгоритмов и реализующих их программ. Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ.

Достоинства и недостатки трех перечисленных способов получения случайных чисел для сравнения представлены в табл. 1. Из этой таблицы видно, что алгоритмический способ получения случайных чисел наиболее рационален на практике при моделировании систем на универсальных ЭВМ.

При моделировании систем на ЭВМ программная имитация случайных воздействий любой сложности сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Вообще говоря, в качестве базового может быть принят любой удобный в случае моделирования конкретной системы S процесс. Однако при дискретном моделировании базовым процессом является последовательность чисел представляющих собой реализации независимых, равномерно распределенных на интервале (0, 1) случайных величин.

Но получить его на цифровой ЭВМ невозможно, так как машина оперирует с п- разрядными числами. Поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0, 1) используют дискретную последовательность 2n случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.

На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений случайной величины используются формулы (алгоритмы). Поэтому такие последовательности, являющиеся по своей сути детерминированными – называются псевдослучайными.

Полученные с помощью генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получаться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных чисел находят алгоритмы вида

x_i+1 = Ф(x_i), (4.1)

представляющие собой рекуррентные соотношения первого порядка, для которых начальное число х₀ и постоянные параметры заданы.

Одной из исторически первых процедур получения псевдослучайных чисел была процедура, получившая название метода серединных квадратов. Недостаток этого метода — наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать.

Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности. Два целых числа a и b конгруэнтны (сравнимы) по модулю.

Например, 1984-4 (mod 10), 5008 = 8 (mod 103) и т. д.

Конгруэнтные процедуры имеет вид

, (4.2)

Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.

Мультипликативный метод. Задает последовательность неотрицательных целых чисел {Xi}, не превосходящих М, по формуле

X_i+1=lX_i (mod M), (4.3)

это частный случай соотношения (4.2) при , m = 0.

В силу детерминированности метода получаются воспроизводимые последовательности. Требуемый объем машинной памяти при этом минимален, а с вычислительной точки зрения необходим последовательный подсчет произведения двух целых чисел, т. е. выполнение операции, которая быстро реализуется современными ЭВМ.

Для машинной реализации наиболее удобна версия M=p^g, где р — число цифр в системе счисления, принятой в ЭВМ (р = 2 для двоичной и р= 10 для десятичной машины); g — число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого, а преобразование целого числа Xi в рациональную дробь из интервала x_i Î (0, 1) осуществляется подстановкой слева от Xi двоичной или десятичной запятой.

Алгоритм построения последовательности для двоичной машины М=2^в сводится к выполнению таких операций :

1. Выбрать в качестве Х0 произвольное нечетное число.

2. Вычислить коэффициент l = 8t ± 3, где t — любое целое положительное число.

3. Найти произведение lХ₀, содержащее не более 2g значащих разрядов.

4. Взять g младших разрядов в качестве первого члена последовательности Х1 а остальные отбросить.

5. Определить дробь x₁=X₁/2^g из интервала (0, 1).

6. Присвоить Х₀ = Х₁.

7. Вернуться к п. 3.

Смешанный метод. Позволяет вычислить последовательность неотрицательных целых чисел {Xi}, не превосходящих М, по формуле

X_i+1=lX_i +m(mod M), (4.4)

т. е. в отличие от мультипликативного метода m ≠ 0. С вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.

Качество конкретной версии такого генератора можно оценить только с помощью соответствующего машинного эксперимента.

В настоящее время почти все пакеты прикладных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруэнтной процедуре.

Поиск по сайту: