 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ⇐ ПредыдущаяСтр 19 из 19
Актуальность работы. Стандартная алгоритмическая модель прогноза месторождений полезных ископаемых с помощью математических схем принятия решений включает в себя два основных этапа работ. На первом этапе, на основе всей имеющейся по району работ картографической информации (геологической, геофизической и т.п.) создается прогнозно-поисковая модель известных (эталонных) рудных объектов, представляющая собой классификатор поисковых признаков, для каждого из которых определена информативность, как количественная характеристика его прогнозно-поисковой значимости. На втором этапе, сначала для каждой элементарной ячейки исследуемой территории вычисляется показатель перспективности, как сумма значений информативности, наблюдаемых в ячейке признаков, а затем те участки территории, у которых наблюдаются относительно высокие значения указанного показателя, выделяются в качестве перспективных на обнаружение новых рудных объектов. Эффективность использования данной алгоритмической модели практически полностью определяется качеством работ первого этапа и во многом зависит от того, каким образом (с помощью какой модели) определяется информативность признаков, включенных в прогнозно-поисковую модель рудных объектов. Любой признак рудного объекта, отражая ту или иную его особенность, содержит о нем определенное количество информации. Вследствие этого в научной литературе неоднократно рекомендовалось при определении информативности признаков использовать математический аппарат теории информации, а за значения информативности принимать, соответственно, количество информации о рудных объектах. Предлагаемые при этом математические модели информационной оценки признаков основаны, как правило, на формуле частной информации “от события к событию”, которая интерпретируется как логарифм отношения вероятности встречи признака на эталонных рудных объектах к вероятности его встречи на исследуемой территории в целом. Вместе с тем, анализ такой традиционной модели информационной оценки признаков показывает, что ее практическое использование может приводить к общей неустойчивости и даже противоречивости получаемых прогнозно-геологических заключений. В соответствии с этим актуальной задачей, направленной на повышение эффективности прогноза месторождений полезных ископаемых с помощью теории информации, является совершенствование математической модели информационной оценки признаков рудных объектов. Цель работы состоит в разработке новой математической модели информационной оценки признаков при прогнозном моделировании рудных объектов, отличительной чертой которой от традиционной модели является детерминированный, а не вероятностно-статистический характер получаемых значений информативности признаков. Задачи исследования:
- анализ существующих подходов к количественному определению информации (комбинаторного, вероятностного, алгоритмического) с позиций совершенствования традиционной математической модели информационной оценки признаков рудных объектов; - разработка нового (синергетического) подхода к количественному определению информации, в котором за информацию принимаются сведения о системном объекте, как едином целом; - разработка новой математической модели информационной оценки признаков рудных объектов, основанной на синергетическом подходе к количественному определению информации. Объект исследования – информационно-количественные аспекты отражения системных объектов, представленных конечным множеством элементов. Предмет исследования – математическая модель информационной оценки признаков рудных объектов. Основная идея работы заключается в реформировании математической модели информационной оценки признаков при прогнозном моделировании рудных объектов таким образом, чтобы получаемые значения информативности были инвариантны, относительно как общей площади проводимых прогнозно-геологических исследований, так и площади тех проявлений признаков, которые не имеют непосредственной взаимосвязи с эталонными рудными объектами. Научные положения, защищаемые автором диссертации: 1. Традиционная математическая модель информационной оценки признаков рудных объектов, основанная на вероятностном подходе к количественному определению информации и учитывающая как общую площадь исследуемой территории, так и площади тех проявлений признаков, которые не имеют непосредственной взаимосвязи с рудными объектами, приводит к неустойчивым решениям поисковых прогнозно-геологических задач. 2. Мерой количества информации о системном объекте, как едином целом, является средняя длина интегративного кода его элементов. При этом системный объект представляет собой обособленное по какому-либо признаку конечное множество элементов в составе некоторой системы, а в качестве интегративного кода элемента выступает поставленная ему в соответствие индивидуальная последовательность символов двоичного алфавита, число которых (длина кода) является функцией от общего количества элементов системного объекта. 3. Математическая модель информационной оценки признаков рудных объектов, основанная на синергетическом подходе к количественному определению информации, обуславливает устойчивое решение прогнозно-геологических задач, инвариантное относительно как общей площади исследуемой территории в целом, так и площади тех проявлений признаков, которые не имеют непосредственной взаимосвязи с эталонными рудными объектами. Обоснованность и достоверность научных положений и выводов, содержащихся в диссертационной работе, подтверждается результатами анализа моделей типичных геологических ситуаций при решении прогнозно-геологических задач и положительными результатами поисковых прогнозно-геологических исследований, проведенных с использованием разработанной математической модели информационной оценки признаков рудных объектов, в двух производственно-геологических организациях. Научная новизна диссертационных исследований: 1. Разработан новый (синергетический) подход к количественному определению информации, отличительной чертой которого от традиционных подходов (комбинаторного, вероятностного, алгоритмического) является отношение к информации как к снимаемой неопределенности отражения (воспроизведения) системных объектов как друг через друга, так и через самих себя. При этом под термином информация понимаютсясведения о системном объекте, как едином целом, а мерой количества информации является средняя длина интегративного кода элементов, образующих системные объекты. 2. Разработана новая математическая модель информационной оценки признаков рудных объектов, отличием которой от традиционной модели является инвариантность, получаемых с ее помощью результатов решения прогнозно-геологических задач, относительно как общей площади исследуемой территории, так и площади тех проявлений признаков, которые не имеют непосредственной взаимосвязи с эталонными рудными объектами. Результаты прогнозных построений при этом являются детерминированными по своей сущности, а не вероятностно-статистическими как при использовании традиционной математической модели. 3. Проведена классификация поисковых прогнозно-геологических задач по виду задания эталонных рудных объектов на два альтернативных рода. При этом прогнозно-геологическая задача является задачей первого рода, если рудные объекты заданы в виде связанных множеств элементарных ячеек территории, охватывающих всю занимаемую ими площадь. Если же рудные объекты заданы в виде единичных элементарных ячеек территории, непосредственно локализующих только рудные тела, то прогнозно-геологическая задача относится к задачам второго рода. Научная значимость проведенных исследований состоит в совершенствовании математического моделирования информационной оценки признаков рудных объектов и развитии количественных аспектов теории информации. Практическая ценность заключается в разработке и производственном использовании новой математической модели информационной оценки признаков при прогнозном моделировании рудных объектов. Реализация работы. На основе полученной в диссертации новой математической модели информационной оценки признаков рудных объектов разработана прогнозно-геологическая система ИНФОТ (информация иотражение), которая прошла апробацию в двух производственно-геологических организациях Министерства природных ресурсов России (Центрально-Уральском федеральном государственном унитарном предприятии и Федеральном государственном унитарном предприятии “Уральская геологическая опытно-методическая экспедиция”) и получила положительную оценку. Личный вклад автора состоит: - в анализе традиционной математической модели информационной оценки признаков рудных объектов и определении путей ее совершенствования; - в моделировании типичных геологических ситуаций при решении прогнозно-геологических задач; - в анализе существующих подходов к количественному определению информации (комбинаторного, вероятностного, алгоритмического) с позиций совершенствования традиционной математической модели информационной оценки признаков рудных объектов; - в разработке нового (синергетического) подхода к количественному определению информации; - в разработке новой математической модели информационной оценки признаков рудных объектов, основанной на синергетическом подходе к количественному определению информации и ее опробовании на моделях типичных геологических ситуаций; - в классификации прогнозно-геологических задач по виду задания эталонных рудных объектов; - во внедрении в производственную практику новой математической модели информационной оценки признаков рудных объектов, основанной на синергетическом подходе к количественному определению информации. Апробация работы. Результаты проведенных исследований и различные аспекты их практического использования неоднократно докладывались и обсуждались на научно-практических форумах различного уровня и тематической направленности: 6-я Уральская научно-практическая конференция “Применение математических методов и ЭВМ при обработке информации на геологоразведочных работах”, Челябинск, 1989; семинар “Количественный прогноз твердых полезных ископаемых”, Алма-Ата, 1990; семинар “Геологическая синергетика”, Алма-Ата, 1991; 5-е Всероссийское совещание-семинар “Компьютерное обеспечение работ по созданию государственной геологической карты Российской Федерации”, Ессентуки, 1998; 6-е Всероссийское совещание-семинар “Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий”, Красноярск, 1999; региональная конференция “Геология и минерально-сырьевые ресурсы европейской территории России и Урала”, Екатеринбург, 2000; межрегиональная научно-практическая конференция “Наука и оборонный комплекс – основные ресурсы российской модернизации”, Екатеринбург, 2002. Публикации. По теме диссертации опубликовано 17 работ. Структура и объем работы. Диссертация состоит из введения, четырех глав и заключения, изложенных на 129 страницах машинописного текста; содержит 17 рисунков, 9 таблиц, список использованных источников из 77 наименований, 2 приложения в виде актов использования результатов диссертационных исследований в производственно-геологических организациях. Автор выражает глубокую благодарность за активное участие в обсуждении результатов исследований и выводов, изложенных в диссертации, и сделанные при этом конструктивные замечания сотрудникам: Центрально-Уральского федерального государственного унитарного предприятия – к.г-м.н. Страшненко Г.И., Мельнику В.В.; государственного федерального унитарного предприятия “Уральская геологическая опытно-методическая экспедиция” – Бронникову Ю.В., Пильникову Е.П., Автонееву С.В., к.г-м.н. Сибирякову Е.А.; Уральской государственной горно-геологической академии – д.г-м.н., проф. Мягкову В.Ф., д.г-м.н., проф. Паняку С.Г.; Уральского государственного университета – д.ф-м.н., проф. Пименову В.Г.; Центральной научной библиотеки Уральского отделения Российской академии наук – д.ф.н., доц. Корюкину В.И., к.ф.н., доц. Шардыко С.К.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ В первой главе сначала дается описание стандартной алгоритмической модели прогноза месторождений полезных ископаемых (МПИ) с помощью теории информации (рис. 1), а затем проводится детальный анализ традиционной математической модели информационной оценки признаков, основанной на вероятностном подходе к количественному определению информации. В основе указанной математической модели лежит формула частной информации “от события к событию”, в оригинале имеющая вид:
где: J(B® A) – частная информация о событии A, содержащаяся в событии B; p(A|B) – условная (апостериорная) вероятность появления события A при наступлении события B; p(A) - априорная вероятность наступления события A. В специализированной литературе по прогнозу МПИ формула (1) неоднократно использовалась для определения количество информации о рудных объектах (событие А), содержащейся в некотором поисковом признаке (событие В) и интерпретировалась при этом следующим образом:
В соответствии с выражением (2) традиционная математическая модель информационной оценки (информативности) какого-либо признака (Pi) относительно эталонных рудных объектов (Э) имеет вид:
где: J(Pi® Э) - значение информативности i-го признака; m(N) - общее количество объектов распознавания (элементарных ячеек, на которые делится площадь прогнозных исследований); m(Э) - общее число эталонных объектов распознавания; m(Pi)- общее число объектов распознавания, на которых проявлен i-й признак;
m(PiЭ) - число эталонных объектов распознавания, на которых проявлен i-й признак. Традиционная модель показателя перспективности (ПП) какой-либо j-ой элементарной ячейки исследуемой территории, в свою очередь, имеет вид:
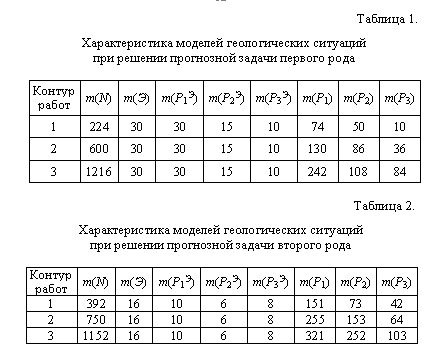
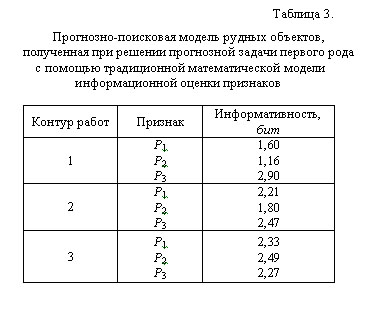
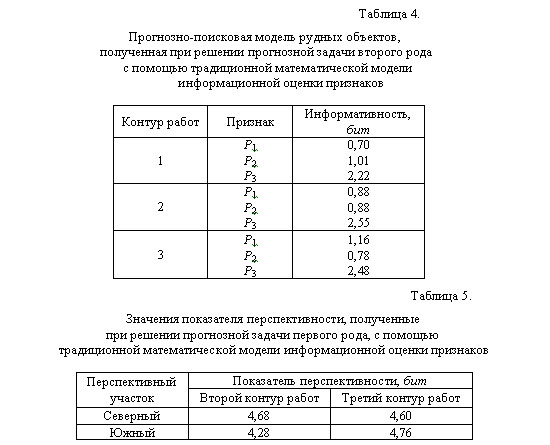
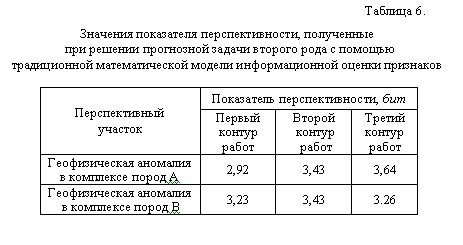
где: n – количество признаков, наблюдаемых в j-ой ячейке. С целью проверки устойчивости и непротиворечивости прогнозно-геологических заключений, получаемых с помощью традиционной математической модели информационной оценки признаков рудных объектов (3), составлены модели типичных геологических ситуаций при решении прогнозных задач первого (рис. 2) и второго (рис. 3) рода. В табл. 1 и 2 даны характеристики моделей геологических ситуаций, представленных на рис. 2 и 3, а в табл. 3 и 4 приведены соответствующие прогнозно-поисковые модели рудных объектов, составленные с помощью традиционной модели информационной оценки признаков (3). Анализ приведенных значений информативности показывает, что они имеют неустойчивый, ситуационный характер. Так как показатель перспективности (4) объектов распознавания является функцией информативности наблюдаемых у них признаков, то, очевидно, что указанная неустойчивость будет распространяться и на его величину, что, в свою очередь, может приводить к противоречивым прогнозным заключениям в целом. Демонстрацией сказанного являются табл. 5 и 6, где приведены значения показателя перспективности различных участков, полученные на основе значений информативности признаков, приведенных в табл. 3 и 4, соответственно.
Из данных табл. 5 следует, что при решении прогнозной задачи первого рода (рис. 2), в пределах второго контура работ, более перспективным является Северный участок, нежели чем Южный. В то же самое время, в том случае, когда площадь исследований ограничена третьим контуром работ, то более перспективным является уже не Северный участок, а Южный. Аналогичная противоречивость прогнозных заключений имеет место и при решении прогнозной задачи второго рода (рис. 3, табл. 6). Здесь, при сравнении перспективности геофизических аномалий, расположенных в комплексах пород А и В и последовательном увеличении площади исследований от первого контура работ до третьего, наблюдается следующее. – На площади первого контура работ более перспективной на обнаружение новых рудных объектов является геофизическая аномалия в комплексе пород В. При проведении прогнозных исследований в пределах второго контура показатель перспективности аномалий в обоих комплексах пород является одинаковым. В том случае, когда площадь прогнозирования увеличивается до размеров третьего контура работ, то более перспективными являются геофизические аномалии в комплексе пород А. Отмеченная противоречивость прогнозных заключений, полученных с помощью традиционной математической модели информационной оценки признаков, обусловлена тем, что эта модель (3) учитывает как общую площадь проводимых прогнозно-геологических исследований, так и площади тех проявлений признаков, которые не имеют непосредственной пространственной взаимосвязи с эталонными рудными объектами. (Такую взаимосвязь на рис. 2 имеют проявления каждого из признаков Р1, Р2, Р3, расположенные в пределах первого контура работ, а на рис. 3 – геофизические аномалии, на площади которых находятся известные рудные объекты.) Чтобы избавиться от неустойчивости значений информативности признаков и потенциального получения противоречивых прогнозных заключений, необходимо при моделировании информационной оценки признаков отказаться от учета общей площади проводимых исследований и аппелировать только к тем (эталонным) проявлениям признаков, которые имеют непосредственную взаимосвязь с эталонными рудными объектами. Иначе говоря, нужно разработать новую математическую модель информационной оценки признаков рудных объектов, основанную, в отличие от традиционной модели, на ином информационно-теоретическом базисе. Так как общую территорию прогнозных исследований можно рассматривать как некоторую систему, а совокупности элементарных ячеек территории, покрывающие эталонные рудные объекты и взаимосвязанные с ними проявления признаков – как соответствующие системные объекты, то при разработке новой математической модели информационной оценки признаков, необходимо, прежде всего, определить количество информации, которую отражают (воспроизводят) относительно друг друга два непосредственно взаимосвязанных между собой системных объекта. Во второй главе рассматриваются традиционные подходы к количественному определению информации (комбинаторный, вероятностный, алгоритмический) с позиций информационно-количественной оценки отражения друг через друга двух непосредственно взаимосвязанных между собой системных объектов. Постановка задачи при этом выглядит следующим образом. Пусть в составе некоторой системы D = {d1, d2, ..., dn} (рис. 4), по отличительным признакам PA и PB выделены три системных объекта A = {a|PA(a)} = {d|PA(d)}, B = {b|PB(b)} = {d|PB(d)}, K = A С гносеологической точки зрения процесс получения информации IA« B познающим субъектом состоит из трех этапов. На первом этапе система D рассматривается в плоскости W (PA) признака PA и выделяется системный объект A. На втором этапе аналогично выделяется системный объект B.
После завершения работ первых двух этапов познающий субъект находится в состоянии неопределенности относительно существования между системными объектами A и B непосредственной взаимосвязи. Рассматривая на третьем этапе системные объекты A и B в совмещенной плоскости W (PA, PB ) признаков PA и PB, познающий субъект выделяет третий системный объект K = A Так как синонимом неопределенности чего-либо, а также отсутствия или недостатка знаний (информации) о чем-либо в настоящее время принято считать энтропию, то информацию IA« B, для отличия от других видов информации, разумно называть негэнтропией отражения. То есть негэнтропия отражения представляет собой информацию об одном системном объекте, как едином целом, отраженную через непосредственно взаимосвязанный с ним другой системный объект. Попытки решить поставленную задачу по определению В третьей главе разрабатывается новый подход к определению количества информации, отличительной чертой которого от традиционных подходов является отношение к информации как к снимаемой неопределенности отражения системных объектов. Этот подход получил название синергетический, что обусловлено тем, что элементы системных объектов участвуют в их отражении всей своей совокупностью, а термин синергетика в переводе с греческого языка буквально означает совместный, согласованно действующий. В синергетическом подходе выводу формулы негэнтропии отражения IA« B предшествует определение количества информации, которую произвольный системный объект отражает о самом себе как едином целом и называемую также самоотражаемой информацией. При этом используется следующий аксиоматический базис (на примере системного объекта А). 1). Под термином информация понимаются сведения о системном объекте, как едином целом. 2). Количество информации IA, самоотражаемой системным объектом А, является монотонно возрастающей функцией от m(A) и, соответственно, для любых двух системных объектов А и В, таких, что m(A) = X, m(B) = X + 1, имеет место неравенство: IA < IB (5) 3). Показателем системного объекта А, как единого целого, является интегративный код его элементов, представляющий собой индивидуальную для каждого элемента последовательность символов какого-либо алфавита, число которых (длина кода) является функцией от общего количества элементов системного объекта. Вывод формулы IA проводится на основе моделирования процесса увеличения числа элементов системного объекта А в виде роста ориентированного дерева (рис. 5), совокупность висячих вершин которого взаимно-однозначно соответствует множеству элементов aÎ A, а максимальное число дуг, выходящих из одной вершины, равно числу символов (n) алфавита, выбранного для составления интегративных кодов. При этом каждой из смежных дуг, в алфавитном порядке, ставится в соответствие свой символ и, как следствие, в качестве индивидуального интегративного кода какого-либо элемента выступает последовательность символов, находящихся на пути движения из начальной вершины дерева в соответствующую данному элементу висячую вершину.
Из анализа рис. 5 следует, что в общем случае все элементы aÎ A по длине L(a) их интегративного кода (числу символов) делятся на два подмножества
Установлено, что
Из совместного анализа выражений (6) и (7) следует, что множества значений
Выявлено, что разность
Так как
Интегративный код любого элемента aÎ A представляет собой определенное символьное сообщение о системном объекте А, как о целостном образовании, вследствие чего величина информации IA интерпретируется также, как средняя длина такого сообщения. Исходя из этого, формула негэнтропии отражения IA« B выводится на основе анализа процесса передачи информации IA по системе информационной связи, в которой отражаемый (A) и отражающий (B) системные объекты являются, соответственно, источником и приемником информации, а связующий объект
Из выражения (8) следует, что негэнтропия IA« B является частью средней длины интегративного кода элементов kÎ K. Так как связующий объект K является подмножеством как системного объекта А, так и системного объекта В, то утверждается, что величина негэнтропии IA« B представляет собой общую часть средней длины интегративного кода элементов aÎ A и bÎ B. В четвертой главе на основе формулы негэнтропии отражения системных объектов (8) получена новая математическая модель информационной оценки признаков рудных объектов и осуществлены ее частные модификации (в зависимости от рода решаемых прогнозно-геологических задач). При этом общая территория прогнозных построений рассматривается как некоторая система, элементами которой являются элементарные ячейки территории. Соответственно, множество эталонных объектов распознавания (Э) и множество элементарных ячеек территории, занятых эталонными проявлениями i–го признака (
Для того, чтобы значения информативности признаков, получаемые с помощью математической модели (9) при решении различных прогнозно-геологических задач, могли иметь объективное сравнение друг с другом, в качестве информативности признаков предложено использовать относительную величину ( - прогнозно-геологическая задача первого рода:
- прогнозно-геологическая задача второго рода:
Чтобы в лексическом отношении отличать модели (10) и (11) как друг от друга, так и от любых других моделей информативности, им даны соответствующие названия: информационный вес отражения ( С помощью математических моделей (10) и (11) проведена прогнозная оценка геологических ситуаций, представленных на рис. 2 и 3, результаты которой приведены в табл. 7–10. Из анализа табл. 7 и 8 следует, что информативности признаков, полученные на основе новой математической модели (9), имеют устойчивый характер и сохраняют свое постоянное значение независимо от площади проводимых работ и тех проявлений признаков, которые не имеют взаимосвязи с эталонными объектами прогноза. Так как показатель перспективности объектов распознавания (4) является функцией информативности признаков, то указанное постоянство распространяется и на его величину, о чем свидетельствуют данные табл. 9 и 10.
Иначе говоря, результаты решения прогнозно-геологических задач, получаемые с помощью новой модели информационной оценки признаков рудных объектов, имеют детерминированный характер (в то время как традиционная модель приводит к вероятностно-статистическим прогнозным заключениям). ЗАКЛЮЧЕНИЕ Диссертация представляет собой комплексную научную работу, сочетающую в себе исследования как методического, так и теоретического характера, направленные, соответственно, на совершенствование математической модели информационной оценки признаков рудных объектов при прогнозе МПИ (главная задача) и на решение теоретических вопросов, связанных с количественными аспектами теории информации. Основные результаты диссертационной работы кратко сводятся к следующему: 1. Показано, что традиционная математическая модель информационной оценки признаков рудных объектов, основанная на вероятностном подходе к количественному определению информации, дает неустойчивые, ситуационные результаты, которые могут приводить к противоречивым прогнозно-геологическим заключениям. 2. Установлено, что традиционные подходы к количественному определению информации (комбинаторный, вероятностный, алгоритмический) не позволяют определить количество информации (негэнтропию отражения), которую отражают относительно друг друга два непосредственно взаимосвязанных между собой системных объекта. 3. Разработан новый (синергетический) подход к количественному определению информации, в котором за информацию принимаются сведения о системных объектах как о целостных образованиях, а мерой информации служит средняя длина интегративного кода их элементов. 4. На основе синергетического подхода к количественному определению информации разработана новая математическая модель информационной оценки признаков при прогнозном моделировании рудных объектов, лишенная недостатков традиционной модели, основанной на вероятностном подходе. 5. Проведена классификация поисковых прогнозно-геологических задач, в зависимости от вида задания эталонных рудных объектов (единичные элементарные ячейки территории или их связанные множества) на два альтернативных рода. На основе полученной в диссертации новой модели информационной оценки признаков рудных объектов разработана прогнозно-геологическая система ИНФОТ, которая неоднократно использовалась при решении производственно-геологических задач, связанных с прогнозом месторождений как рудных (золото), так и нерудных (особо чистый кварц) полезных ископаемых в масштабе 1:50000. При этом работы на особо чистый кварц проводились дважды, и в обоих случаях на перспективных участках, выделенных с помощью системы ИНФОТ, заверочными работами были выявлены неизвестные ранее промышленно-значимые объекты. В результате прогнозных работ на рудное золото, в свою очередь, были выявлены три новые перспективные площади, не охваченные ранее проведенными поисковыми работами масштаба 1:10000. При этом на территории ранее проведенных поисковых работ, получивших отрицательные результаты, каких-либо аномальных повышений показателя перспективности не выявлено. Приведенные результаты неоднократного использования системы ИНФОТ в производственных условиях свидетельствуют, что математическая модель информационной оценки признаков рудных объектов, основанная на синергетическом подходе к количественному определению информации, является работоспособной и может быть рекомендована геологическим организациям для широкого применения. По теме диссертации опубликованы следующие работы: 1. Вяткин В.Б. Новые информационные характеристики картографических признаков // Тезисы докладов 6-й Уральской научно-практической конференции "Применение математических методов и ЭВМ при обработке информации на геологоразведочных работах." – Челябинск, 1989. – С. 143-145. 2. Вяткин В.Б. Информационный вес отражения и его возможности при прогнозно-геологических исследованиях // Тезисы докладов семинара "Количественный прогноз твердых полезных ископаемых". – Алма-Ата: КазИМС, 1990. – С. 25-26. 3. Вяткин В.Б. Совместный анализ двух информационных подходов к исследованию системы "объект-признак" // Тезисы докладов семинара "Геологическая синергетика". – Алма-Ата: КазИМС, 1991. – С. 7-9. 4. Вяткин В.Б. К вопросу информационной оценки признаков при прогнозно-геологических исследованиях // Известия Уральского горного института. Сер.: Геология и геофизика. – 1993. – Вып.2. – С. 21-28. 5. Вяткин В.Б. Теория информации и проблема негэнтропийной оценки признаков // Техногенез и экология: Информационно-тематический сборник – Екатеринбург: УГГГА, 1998. – 6. Вяткин В.Б. К вопросу классифицирования прогнозно-поисковых задач по степени геологической корректности их постановки. // Компьютерное обеспечение работ по созданию государственной геологической карты Российской федерации: Материалы 5-го Всероссийского совещания-семинара. – Ессентуки, 1998 – С. 114-116. 7. Вяткин В.Б. Информационные прогнозно-геологические антиномии. // Компьютерное обеспечение работ по созданию государственной геологической карты Российской федерации: Материалы 5-го Всероссийского совещания-семинара. – Ессентуки, 1998 – С. 116-119. 8. Вяткин В.Б. Информационно-энтропийный анализ отражения системных объектов // Техногенез и экология: Информационно-тематический сборник – Екатеринбург: УГГГА, 1999 – 9. Вяткин В.Б. Информативность признаков: необходимость смены парадигмы // Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий: Материалы 6-го Всероссийского совещания-семинара по компьютерным технологиям – Красноярск, 1999 – С. 56-60. 10. Вяткин В.Б. Теоретические основы системы информационного анализа ИНФОТ и ее функциональные возможности при прогнозно-геологических исследованиях // Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий: Материалы 6-го Всероссийского совещания-семинара по компьютерным технологиям – Красноярск, 1999 – С. 181-186. 11. Вяткин В.Б., Автонеев С.В. Выделение новых потенциально золоторудных площадей в пределах Краснотурьинского рудного узла с помощью системы ИНФОТ // Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий: Материалы 6-го Всероссийского совещания-семинара по компьютерным технологиям – Красноярск, 1999 – С. 175-178. 12. Вяткин В.Б., Страшненко Г.И., Мельник В.В. Прогнозная оценка Сакмарского кварценосного района с помощью системы ИНФОТ // Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий: Материалы 6-го Всероссийского совещания-семинара по компьютерным технологиям – Красноярск, 1999 – 13. Вяткин В.Б. Оценка информативности признаков: два подхода, две идеологии // Геология и минерально-сырьевые ресурсы Европейской территории России и Урала: Материалы региональной конференции – Екатеринбург, 2000 – С. 265-266. 14. Вяткин В.Б. Количественное прогнозирование месторождений полезных ископаемых: вчера, сегодня, завтра // Геология и минерально-сырьевые ресурсы Европейской территории России и Урала: Материалы региональной конференции – Екатеринбург, 2000 – С. 268-269. 15. Вяткин В.Б. Прогнозно-металлогеническая оценка территорий с помощью системы информационного анализа “ИНФОТ” // Геология и минерально-сырьевые ресурсы Европейской территории России и Урала: Материалы региональной конференции – Екатеринбург, 2000 – С. 267-268. 16. Вяткин В.Б. Информационный закон отражения системных объектов. // Проблемы методологии междисциплинарных исследований и комплексного обеспечения научно-исследовательской деятельности. Вып.3. – Екатеринбург: УрО РАН, 2001. – С. 24-42. 17. Вяткин В.Б. Синергетическая теория информации: общая характеристика и примеры использования // Материалы межрегиональной научно-практической конференции “Наука и оборонный комплекс – основные ресурсы российской модернизации” – Екатеринбург: УрО РАН, 2002 – С. 361-390.
NB: С дальнейшим развитием синергетического подхода к количественному определению информации можно познакомиться на сайте автора диссертации, расположенном по адресу: Дата публикации: 2 июля 2008
Поиск по сайту: |
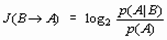 , (1)
, (1)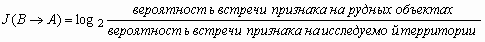 (2)
(2)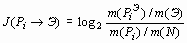 , (3)
, (3)
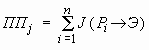 , (4)
, (4)

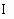 B = {k|PA(k), PB(k)}. Количество элементов в составе A, B, K равно m(A), m(B), m(K), соответственно. Считается, что системные объекты A и B непосредственно взаимосвязаны между собой, если K ¹ Æ (рис. 4, б,в,г,д). Требуется определить, чему равно количество информации IA« B = f ((m(A), m(B), m(K)), отражаемой системными объектами A и B относительно друг друга, как единого целого, при наличии между ними непосредственной взаимосвязи.
B = {k|PA(k), PB(k)}. Количество элементов в составе A, B, K равно m(A), m(B), m(K), соответственно. Считается, что системные объекты A и B непосредственно взаимосвязаны между собой, если K ¹ Æ (рис. 4, б,в,г,д). Требуется определить, чему равно количество информации IA« B = f ((m(A), m(B), m(K)), отражаемой системными объектами A и B относительно друг друга, как единого целого, при наличии между ними непосредственной взаимосвязи.
 B и тем самым снимает (ликвидирует) указанную неопределенность и получает информацию IA« B, которую системные объекты A и B отражают друг о друге, как о целостных образованиях.
B и тем самым снимает (ликвидирует) указанную неопределенность и получает информацию IA« B, которую системные объекты A и B отражают друг о друге, как о целостных образованиях.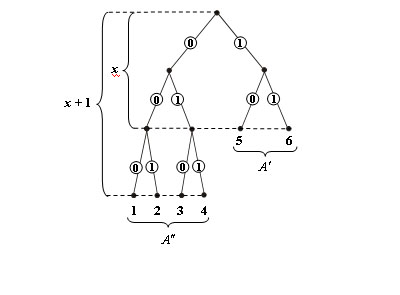
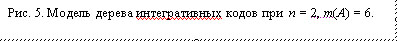
 и
и 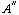 , таких, что
, таких, что 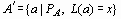 ,
, 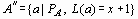 , где
, где 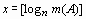 - целочисленная часть
- целочисленная часть 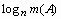 . Соответственно, средняя длина
. Соответственно, средняя длина 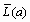 интегративного кода элементов aÎ A равна:
интегративного кода элементов aÎ A равна: .
. , (6)
, (6)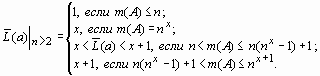 (7)
(7)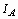 , то есть:
, то есть: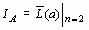 .
. на всем множестве значений
на всем множестве значений 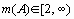 ограничена постоянной величиной y :
ограничена постоянной величиной y :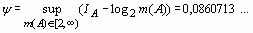
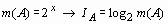 , а
, а 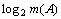 является монотонно возрастающей функцией от m(A), значения которой удовлетворяют информационной аксиоме (5), то, учитывая значение постоянной y , в практическом отношении (в том числе для простоты расчетов) принимается эквивалентность:
является монотонно возрастающей функцией от m(A), значения которой удовлетворяют информационной аксиоме (5), то, учитывая значение постоянной y , в практическом отношении (в том числе для простоты расчетов) принимается эквивалентность: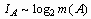
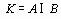 выступает в качестве передающей среды или канала связи. При этом адресатом является познающий субъект. В результате указанного анализа формула негэнтропии отражения системных объектов получена в следующем виде:
выступает в качестве передающей среды или канала связи. При этом адресатом является познающий субъект. В результате указанного анализа формула негэнтропии отражения системных объектов получена в следующем виде: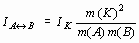 . (8)
. (8)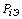 ), образуют системные объекты, непосредственно взаимосвязанные между собой подмножеством эталонных объектов (
), образуют системные объекты, непосредственно взаимосвязанные между собой подмножеством эталонных объектов ( 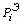 ), фиксируемых i–м признаком, то есть
), фиксируемых i–м признаком, то есть  . В этих обозначениях математическая модель информационной оценки i–го признака, согласно (8), имеет вид:
. В этих обозначениях математическая модель информационной оценки i–го признака, согласно (8), имеет вид: . (9)
. (9) ) информационной оценки (9). При этом, при решении прогнозно-геологических задач второго рода, за множество
) информационной оценки (9). При этом, при решении прогнозно-геологических задач второго рода, за множество 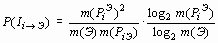 ; (10)
; (10)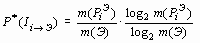 . (11)
. (11)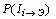 ) и рудоотражающий вес (
) и рудоотражающий вес ( 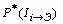 ) признаков.
) признаков.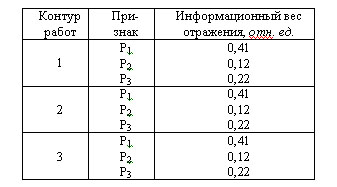

 Минералогия
Минералогия