|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Распределение электрического поля и потенциала в барьере Шоттки
Рассмотрим более детально, как меняются электрическое поле и потенциал в области пространственного заряда контакта металл – полупроводник в виде барьера Шоттки. Для определенности будем рассматривать полупроводник n‑типа. За знак приложенного напряжения примем знак напряжения, приложенного к металлическому электроду, полупроводниковый электрод считаем заземленным. Вне зависимости от полярности напряжения для барьерных структур все внешнее напряжение будет приложено к области пространственного заряда, поскольку в этой области концентрация свободных носителей существенно меньше, чем в других областях барьера Шоттки. Связь электрического поля и потенциала для любых материалов с пространственно распределенным объемным зарядом описывается уравнением Пуассона. В одномерном приближении это уравнение имеет вид:
где y(x)– зависимость потенциала от координаты, r(x) – плотность объемного заряда, es – диэлектрическая проницаемость полупроводника, e0 – диэлектрическая постоянная. Заряд в области пространственного заряда барьера Шоттки для полупроводника n‑типа обусловлен зарядом ионизованных доноров с плотностью ND+. Поэтому
При интегрировании уравнения Пуассона учтем, что величина электрического поля
или Проведем интегрирование уравнения (2.33). Выберем константу интегрирования из расчета, что при x = W электрическое поле Е равно нулю,
Из соотношения (2.34) следует, что электрическое поле Е максимально на границе металл – полупроводник (x = 0), линейно спадает по области пространственного заряда и равно нулю на границе ОПЗ – квазинейтральный объем полупроводника (x = W). Для нахождения распределения потенциала (а следовательно, и зависимости потенциальной энергии от координаты) проинтегрируем еще раз уравнение (2.34) при следующих граничных условиях: x = W, y(W) = 0. Получаем (рис. 2.6):
Максимальное значение потенциала реализуется при x = 0 и составляет:
В этом случае можно рассчитать значение ширины обедненной области W, подставляя соотношение (2.36) в (2.35):
Соотношение (2.37) является очень важным для барьерных структур. В дальнейшем будет показано, что это уравнение является универсальным и описывает зависимость ширины обедненной области W от приложенного напряжения VG и легирующей концентрации ND для большинства барьерных структур. На рисунке 2.6 приведена диаграмма, иллюстрирующая распределение электрического поля и потенциала в барьере Шоттки при обратном смещении, рассчитанных на основании соотношений (2.34) и (2.35).
Рис. 2.6. Диаграмма, иллюстрирующая распределение электрического поля и потенциала в барьере Шоттки: а) структура барьера Шоттки при обратном смещении; б) распределение электрического поля в ОПЗ; в) распределение потенциала в ОПЗ 2.9. Вольт‑амперная характеристика барьера Шоттки Для рассмотрения вольт‑амперной характеристики (ВАХ) барьера Шоттки воспользуемся диодным приближением. Вместо критерия
Подставляя это выражение в (2.5) и (2.7), получаем:
где υ0 – тепловая скорость электронов, равная ns – поверхностная концентрация в полупроводнике на границе с металлом n0 – равновесная концентрация основных носителей в полупроводнике, равная В условиях равновесия VG = 0 ток из полупроводника в металл
В более компактной форме ВАХ записывается в виде:
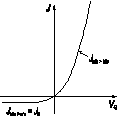
На рисунке 2.7 приведена вольт‑амперная характеристика барьера Шоттки.
Рис. 2.7. Вольт-амперная характеристика барьера Шоттки Вольт‑амперная характеристика барьера Шоттки имеет ярко выраженный несимметричный вид. В области прямых смещений ток экспоненциально сильно растёт с ростом приложенного напряжения. В области обратных смещений ток от напряжения не зависит. В обеих случаях, при прямом и обратном смещении, ток в барьере Шоттки обусловлен основными носителями – электронами. По этой причине диоды на основе барьера Шоттки являются быстродействующими приборами, поскольку в них отсутствуют рекомбинационные и диффузионные процессы. Несимметричность вольт-амперной характеристики барьера Шоттки – типичная для барьерных структур. Зависимость тока от напряжения в таких структурах обусловлена изменением числа носителей, принимающих участие в процессах зарядопереноса. Роль внешнего напряжения заключается в изменении числа электронов, переходящих из одной части барьерной структуры в другую.
Поиск по сайту: |
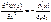 ,(2.30)
,(2.30)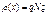 .(2.31)
.(2.31) :
: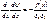 ,(2.32)
,(2.32)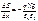 . (2.33)
. (2.33)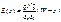 .(2.34)
.(2.34) (2.35)
(2.35) , при
, при 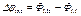 . (2.36)
. (2.36) . (2.37)
. (2.37)
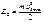 для барьера Шоттки воспользуемся для перехода электронов из полупроводника в металл выражением:
для барьера Шоттки воспользуемся для перехода электронов из полупроводника в металл выражением: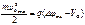 .(2.38)
.(2.38)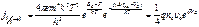 ,(2.39)
,(2.39) ,
, ,
, [6, 17].
[6, 17]. уравновешивается током из металла в полупроводник
уравновешивается током из металла в полупроводник 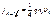 . При приложении напряжения этот баланс нарушается и общий ток будет равен сумме этих токов. Следовательно, вольт‑амперная характеристика барьера Шоттки будет иметь вид:
. При приложении напряжения этот баланс нарушается и общий ток будет равен сумме этих токов. Следовательно, вольт‑амперная характеристика барьера Шоттки будет иметь вид: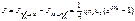 ; (2.40)
; (2.40) . (2.41)
. (2.41)