 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Распределение квантовых состояний в зонах
Стационарные состояния электрона в идеальном кристалле характеризуются квазиимпульсом р. Запишем принцип неоднородностей Гейзенберга для квазиимпульсов dpx, dpy и dpz:
Перемножим соответственно левые и правые части этих соотношений. Получим
где
Рис. 1.3. Диаграмма для расчета плотности квантовых состояний: а) распределение электронов по энергии в зоне проводимости; б) зона Бриллюэна для расчета плотности состояний Определим число квантовых состояний в зоне проводимости в узком интервале энергий от Е до Е + dЕ, рассчитанное на единицу объема кристалла. Его можно представить в виде N(E)dE, где N(E) есть плотность состояний. Вблизи дна зоны проводимости для случая изотропного параболического закона дисперсии энергия электрона
где ЕC – энергия, соответствующая дну зоны проводимости. Для удобства эффективную массу электрона mn будем писать без звездочки. Из (1.4) получим
Отсюда
Аналогичная формула получается и для валентной зоны, но только вместо (Е – ЕC) напишем (ЕV – Е), а вместо mn – эффективную массу дырки mp. Как видно из (1.6), плотность квантовых состояний возрастает по мере удаления от дна зоны проводимости.
Поиск по сайту: |
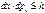
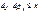 ,
,  (1.1)
(1.1) , (1.2)
, (1.2)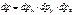 и
и 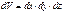 , то есть dp – это некоторый объем в пространстве квазиимпульсов px, py, pz, то есть внутри зоны Бриллюэна, а dV – некоторый объем внутри полупроводника. При этом объем dV – не обязательно бесконечно малая величина. Он может быть и конечным. Для расчета концентраций носителей заряда (то есть числа носителей в единице объема полупроводника) выделим внутри кристалла единичный объем dV = 1 см3. Тогда из (1.2) получим dp £ h3. То есть внутри объема dp = h3 в зоне Бриллюэна может иметь место только одно квантовое состояние, которое как бы размыто по всему этому объему. Итак, h3 – это объем одной “квартирки” в зоне Бриллюэна, в которую можно поместить только два электрона с разными спинами, и не более. Поэтому число квантовых состояний, соответствующее элементу объема dp в зоне Бриллюэна и рассчитанное на единицу объема кристалла, равно
, то есть dp – это некоторый объем в пространстве квазиимпульсов px, py, pz, то есть внутри зоны Бриллюэна, а dV – некоторый объем внутри полупроводника. При этом объем dV – не обязательно бесконечно малая величина. Он может быть и конечным. Для расчета концентраций носителей заряда (то есть числа носителей в единице объема полупроводника) выделим внутри кристалла единичный объем dV = 1 см3. Тогда из (1.2) получим dp £ h3. То есть внутри объема dp = h3 в зоне Бриллюэна может иметь место только одно квантовое состояние, которое как бы размыто по всему этому объему. Итак, h3 – это объем одной “квартирки” в зоне Бриллюэна, в которую можно поместить только два электрона с разными спинами, и не более. Поэтому число квантовых состояний, соответствующее элементу объема dp в зоне Бриллюэна и рассчитанное на единицу объема кристалла, равно  – то есть числу “квартирок” в объеме dp. При заполнении зоны проводимости электронами заполняются вначале самые нижние уровни. Зона проводимости – одномерная относительно энергии (рис. 1.3а). Зона Бриллюэна – трехмерная (px, py, pz) (рис. 1.3б). Заполнение зоны Бриллюэна начинается с самых малых значений квазиимпульса p. Поэтому в качестве dp надо выбрать элемент объема, заключенный между двумя очень близкими изоэнергетическими поверхностями (см. рис. 1.3б). Внутри этого тонкого шарового слоя радиусом p и толщиной dp число квантовых состояний будет равно:
– то есть числу “квартирок” в объеме dp. При заполнении зоны проводимости электронами заполняются вначале самые нижние уровни. Зона проводимости – одномерная относительно энергии (рис. 1.3а). Зона Бриллюэна – трехмерная (px, py, pz) (рис. 1.3б). Заполнение зоны Бриллюэна начинается с самых малых значений квазиимпульса p. Поэтому в качестве dp надо выбрать элемент объема, заключенный между двумя очень близкими изоэнергетическими поверхностями (см. рис. 1.3б). Внутри этого тонкого шарового слоя радиусом p и толщиной dp число квантовых состояний будет равно: . (1.3)
. (1.3)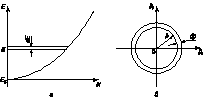
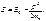 (1.4)
(1.4) , то есть
, то есть  и
и 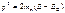 . Подставляем в (1.3), имеем
. Подставляем в (1.3), имеем . (1.5)
. (1.5)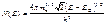 . (1.6)
. (1.6)