 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коэффициент переноса. Фундаментальное уравнение теории транзисторов
Коэффициент передачи эмиттерного тока a характеризует изменение коллекторного тока Iк при вызвавшем его изменении эмиттерного тока Iэ. Ток коллектора обусловлен дырками, дошедшими от эмиттерного перехода до коллекторного. Поэтому важны доля дырок, дошедших до коллекторного перехода и нерекомбинировавших в базе, и доля дырочного тока в эмиттерном токе.
Зависимость коэффициента инжекции g от параметров биполярного транзистора была получена ранее. Рассмотрим зависимость коэффициента переноса Из уравнения непрерывности
следует, что в стационарном режиме
Решение дифференциального уравнения (5.11) в общем виде будет иметь следующий вид:
Запишем граничные условия для (5.11) исходя из того, что заданы эмиттерный ток Jэр = g Jэ и коллекторное напряжение Uк.
Найдем коэффициенты А1 и А2. Продифференцировав уравнение в решении (5.12) по x, получаем:
с учетом граничных условий (5.13) имеем:
с учетом граничных условий (5.15а) имеем:
Решая совместно уравнения (5.15а, б), находим коэффициенты A1 и A2. Затем подставляем A1 и A2 в уравнение (5.12) и получаем следующее выражение для распределения концентрации инжектированных дырок рn(х) по базе биполярного транзистора:
Последний сомножитель в квадратных скобках уравнения (5.16) всегда меньше единицы. Наконец, разложив гиперболический синус sh(x) и гиперболический косинус ch(х) в ряд при условии x < W << Lр, получаем закон распределения дырок рn(х) по базе биполярного транзистора в первом приближении:
Выражение (5.17) показывает, что в первом приближении распределение дырок рn(х) по толщине базы линейно. Этот вывод понятен и по физическим соображениям. Поскольку ток в базовой области диффузионный и примерно постоянен по ширине базы (так как рекомбинация мала), градиент концентрации дырок постоянен: Так как коэффициент переноса
то
Для того, чтобы точно определить коллекторный ток Jк, продифференцируем уравнение (5.16) для концентрации дырок р(х) и рассчитаем это выражение при х = W. Тогда
Умножив (5.18) на qDS, получаем с учетом того, что гиперболический
Следовательно, коэффициент переноса
Уравнение (5.20) является очень важным соотношением для биполярных транзисторов и по этой причине называется фундаментальным уравнением теории транзисторов. Разлагая гиперболический косинус ch(x) в ряд при условии, что x < W, и используя первый член в этом разложении, получаем:
Полагая значение W = 0,2L, получаем:
Таким образом, значение коэффициента переноса Поскольку коэффициент передачи a определяется произведением коэффициентов инжекции g и переноса
Поиск по сайту: |
 .(5.9)
.(5.9)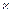 от параметров биполярного транзистора.
от параметров биполярного транзистора. (5.10)
(5.10) .(5.11)
.(5.11) .(5.12)
.(5.12) ,(5.13)
,(5.13) .(5.14)
.(5.14) ,
, ,(5.15а)
,(5.15а)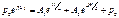 .(5.15б)
.(5.15б) .(5.16)
.(5.16) .(5.17)
.(5.17) .
. ,
, .
. . (5.18)
. (5.18) стремится к единице,
стремится к единице, . (5.19)
. (5.19) .(5.20)
.(5.20) .(5.21)
.(5.21) .
.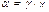 , то у сплавных транзисторов, где ширина базы составляет W = 10¸20 мкм, в коэффициенте передачи a главную роль играет коэффициент переноса
, то у сплавных транзисторов, где ширина базы составляет W = 10¸20 мкм, в коэффициенте передачи a главную роль играет коэффициент переноса