 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Концентрация носителей заряда и положение уровня Ферми
Электроны, как частицы, обладающие полуцелым спином, подчиняются статистике Ферми – Дирака. Вероятность того, что электрон будет находиться в квантовом состоянии с энергией Е, выражается функцией Ферми – Дирака:
Здесь F – электрохимический потенциал, или уровень Ферми. Из (1.7) видно, что уровень Ферми можно определить как энергию такого квантового состояния, вероятность заполнения которого равна ½. Вид функции Ферми – Дирака схематически показан на рисунке 1.4. При Т = 0 она имеет вид разрывной функции. Для E < F она равна 1, а значит, все квантовые состояния при E < F заполнены электронами. Для E > F функция f = 0 и соответствующие квантовые состояния совершенно не заполнены. При Т > 0 функция Ферми изображается непрерывной кривой и в узкой области энергий, порядка нескольких kT, в окрестности точки E = F быстро изменяется от 1 до 0. Размытие функции Ферми тем больше, чем выше температура. Вычисление различных статистических величин значительно упрощается, если уровень Ферми F лежит в запрещенной зоне энергий и удален от края зоны ЕC хотя бы на 2kT (в некоторых учебниках пишут ЕC – Е > kT). Тогда в распределении (1.7) единицей в знаменателе можно пренебречь и оно переходит в распределение Максвелла – Больцмана классической статистики. Это случай невырожденного полупроводника:
Концентрация электронов в зоне проводимости равна:
Рис. 1.4. Функция распределения плотности состояний в зоне проводимости N(E), функции Ферми – Дирака f и Больцмана fБ Отметим, что в качестве верхнего предела в написанном интеграле мы должны были бы взять энергию верхнего края зоны проводимости. Но так как функция f для энергий E > F экспоненциально быстро убывает с увеличением E, то замена верхнего предела на бесконечность не меняет значения интеграла. Подставляем в (1.9) выражения (1.6) и (1.8). Расчет интеграла несложен. Получим:
где
Величина NC получила название эффективной плотности состояний в зоне проводимости. В случае невырожденного полупроводника, когда уровень Ферми лежит выше потолка валентной зоны хотя бы на 2kT, то есть F – EC > 2kT (в некоторых учебниках пишут F – EC > kT), функция Ферми – Дирака для дырок fp имеет вид:
а концентрация дырок в валентной зоне
где EV – энергия, соответствующая потолку валентной зоны, а NV рассчитывается по уравнению (1.11), если вместо mn взять эффективную массу дырки mp. Величина NV – эффективная плотность состояний в валентной зоне. Отметим, что в (1.9) перед интегралом появился множитель 2, что связано с тем, что на каждом уровне энергии могут находиться два электрона с противоположными спинами (принцип Паули). Для расчета n и p по уравнениям (1.10) и (1.13) необходимо знать положение уровня Ферми F. Однако произведение концентраций электронов и дырок для невырожденного полупроводника не зависит от уровня Ферми, хотя зависит от температуры:
Это уравнение используется для расчета p при известном n или, наоборот, для расчета n при известном p. Величина ni при некоторых температурах для конкретных полупроводников приводится в справочниках.
Поиск по сайту: |
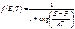 (1.7)
(1.7)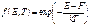 . (1.8)
. (1.8)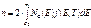 . (1.9)
. (1.9)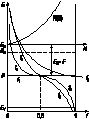
 (1.10)
(1.10)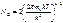 . (1.11)
. (1.11)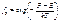 , (1.12)
, (1.12)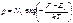 , (1.13)
, (1.13) . (1.14)
. (1.14)