 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Бесконечно малые и бесконечно большие функции.
Функция
Функция
Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности. Бесконечно малая функция: Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Док-во:
Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. Док-во:
Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая. Следствие: произведение б.м.ф. на число есть функция бесконечно малая. Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая. Док-во:
Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот. Док-во:
Односторонние пределы.
Предел слева записывают так: Аналогично определяется предел функции справа:
Пределы функции слева и справа называются односторонними пределами. Сравнение бесконечно малых. Две б.м.ф. сравниваются между собой с помощью их отношения: 1. если 2. если 3. если 4. если Таковы же правила сравнения б.м.ф. при Эквивалентные бесконечно малые:
Теоремы о пределах. Теорема: если существует Теорема: если 1) 2) 3) Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть Примечание 2: Теорема: если Следствие: если Теорема: если Теорема (о сжатой переменной): если Теорема (о пределе сложной функции): Пусть: х0,
Сама теорема: Если
Поиск по сайту: |
 называется бесконечно большой при
называется бесконечно большой при  ,если для любого числа M>0 существует число
,если для любого числа M>0 существует число  =
=  , выполняется неравенство
, выполняется неравенство  . Записывают
. Записывают  . Коротко:
. Коротко:
 ,если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству
,если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству 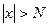 , выполняется неравенство
, выполняется неравенство 
 : для любого числа
: для любого числа  >0 найдется число
>0 найдется число  .
. )>0 такое, что при
)>0 такое, что при  выполняется неравенство
выполняется неравенство  .
.
 .
.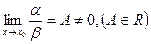 , то
, то  и
и 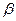 называются бесконечно малыми одного порядка.
называются бесконечно малыми одного порядка. то
то  то
то 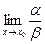 не существует, то
не существует, то  и
и  .
.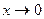
 ,
,  и
и  и они равны между собой, то существует
и они равны между собой, то существует  =
=  ,
,  , то =>
, то =>


 .
.
 и существуют конечные пределы, когда
и существуют конечные пределы, когда  .
. и существуют конечные пределы
и существуют конечные пределы 
 => существует:
=> существует:  , U=f(x),
, U=f(x),  .
.
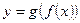 и существуют конечные пределы
и существуют конечные пределы  и
и  , то
, то 