 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Скалярное произведение векторов. Определение. Вычисление. Свойства.
Скалярное произведение векторов - число = произвед длин на косинус между ними. Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось. Свойства: 1.a*b=b*a 2. (C*a)*b=C*(a*b) 3. a(b+c)=a*c+b*c; 4. 5. (a, b) = 0 => 6. ij = jk = kj = 0. Теорема 1: в пространстве R3 в ортонормированном базисе
Следствие из Т1: Для вектора Механический смысл скалярного произведения: Пусть
13. векторное произведение векторов. Определение. Вычисление. Свойства. Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой. Векторное произведение вектора a на b - это c, который: 1)с перпендикулярно a и b; 2)имеет длину, численно равную площади параллельного, параллелограмма на векторах |c|=|a|*|b|*sinσ; 3) векторы a, b, с образ правую тройку. Замечание: Из определения вытекает след соотношения между ортами ijk: 1. i*j=k; 2. j*k=i; 3. k*i=j; Свойства: 1)векторное произ при перестановке множителей меняет знак. ( 2)два ненулевых вектора коллинеарны, когда их векторное произв =0. Пункты: 1)условие коллиниарности: a//b => a*b=0; 2)нахождение S параллелограмма и S треуг. Sпар= 3)определение момента силы. |M|=|F|*|S|. Теорема:
Смешанное произведение векторов. Определение. Вычисление. Свойства. Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку. Свойства: 1)смешанное произв не меняется при циклической перестановке его множителей. ( 2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей 3)смешанное произ ненулевых векторов =0 тога, когда они компланарны. Смешанное произ векторов = определителю 3-его порядка, составленного из координат перемноженных векторов. Приложение. 1)определение взаимных ориентаций векторов в пространстве: если 2)комплонарность векторов: 3)Геометрический смысл: Vпараллелепипеда= Вычисление:
Прямая на плоскости. Простейшей из линий является прямая. Разным способам задания прямой соответствует в прямоугольной система координат разные виды ее уравнений. 1. Уравнение прямой с угловым коэффициентом: Пусть: tg Число tg
Поиск по сайту: |



 :
:

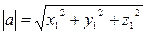
 :
: 
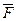 - сила, которая перемещает тело в направлении вектора S ( на длину
- сила, которая перемещает тело в направлении вектора S ( на длину  ) =>
) =>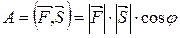
 )
) sin
sin  . Sтр=0,5*
. Sтр=0,5* 
 ,
, 

 .
. >0 (
>0 (  ,
, 


 =k,
=k,  , тогда: y = kx + b.
, тогда: y = kx + b.