 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Векторы на плоскости и в пространстве. Операции над векторами.
Вектор– направленный отрезок, т.е. раз есть слово отрезок, значит есть начало и конец. 1. перенос отрезка при помощи параллельного переноса, не изменяет вектор. 2. вектор задается «длиной вектора» и направления. 3. если у вектора изменить направление на противоположное, то получаем противоположный вектор. 4. нулевой вектор – вектор, длина которого = 0 или начальная конечная точки совпадают. ( у нулевого вектора направление неопределенно). Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой. Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные. Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости. Примечание: два вектора в пространстве всегда компланарны. Примечание: два вектора называются равными, если они сонаправлены и равны по длине. Линейные операции над векторами: 1. умножение вектора на число: Результатом будет вектор, коллинеарный исходному (соноправленный в случае положительного множителя и противоположно-направленный – в случае отрицательного множителя), длина которого равна произведению модуля числового множителя на длину исходного модуля. 2. сумма двух векторов: Есть вектор, получаемый из слагаемых при помощи правила параллелограмма или правила треугольника.
11. Коллинеарность и компланарность. Базис. Координаты. Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой. Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные. Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости. Примечание: два вектора в пространстве всегда компланарны. Примечание: два вектора называются равными, если они сонаправлены и равны по длине. Базис пространства -совокупность лин независ векторов, по которым можно разложить любой вектор этого пр-ва. Базис 3x мерного пр-ва образует любая тройка некомпланарных векторов пр-ва. Если Примечание: для конкретно-заданного базиса не всегда просто бывает найти коэффициент Проще всего это сделать когда базис является ортонормированным. Понятие ортонормированности распадается на понятия ортогональности и нормированности. ( перпендикулярность и длина=1). В 3-х мерном пространстве Ортонормированный базис состоит из 3-х взаимноперпендикулярных векторов, длина каждого из которых = 1.
Поиск по сайту: |
 образуют базис в пространстве, то любой вектор
образуют базис в пространстве, то любой вектор  из этого пространства может быть представлен:
из этого пространства может быть представлен: 
 .
.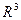 ортогональный базис состоит из 3 взаимноперпендикулярных векторов.
ортогональный базис состоит из 3 взаимноперпендикулярных векторов.