Операція перетину множин та основні властивості (закони) цієї операції.

5. Розглянемо дві множини А={1,2,3,4} і B={2,4,6,8} та утворимо третю множину С={2,4}. Із яких елементів складається множина С? – із елементів, які входять в кожну із множину, тобто із спільних елементів цих множин. Таку множину називають перетином множин А та В і позначають символом АÇВ=С.

Означення: перетином двох множин А і В називається така третя множина АÇВ, яка складається із спільних елементів А та В.

Символічно це означення можна записати так: AÇB={х/хÎA і хÎB}. З допомогою діаграм Ейлера-Венна перетин множин А і В зображено на малюнку № 1.8.

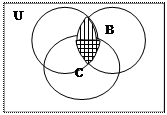
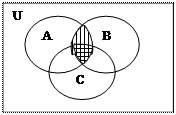
Малюнок № 1.8. Перетин множин AÇB.

Означення перетину можна поширити на випадок трьох і будь-якої скінченної кількості множин. Операція перетину множин підкоряється таким законам:

1. AÇÆ=Æ.

2. AÇИ=A.

3. AÇA=A - закон ідемпотентності (незмінності).

4. AÇB=BÇA - переставний (комутативний).

5. АÇ(ВÇС)=(АÇВ)ÇС – сполучний (асоціативний).

6. АÇ(ВÈС)=(АÇВ)È(АÇС) – розподільний (дистрибутивний) закон перетину відносно об’єднання.

7. АÈ(ВÇС)=(АÈВ)Ç(АÈС) – розподільний (дистрибутивний) закон об’єднання відносно перетину.

Справедливість законів 1-3 легко обґрунтувати, виходячи із означення операції перетину, а закони 4-7 слід довести, використовуючи міркування чи діаграми Ейлера-Венна. Доведемо асоціативний закон операції перетину (AÇB)ÇС=AÇ(BÇС), використовуючи діаграми Ейлера-Венна (див. малюнок № 1.9.). На лівій діаграмі спочатку заштрихуємо вертикальними лініями множину AÇB, а горизонтальними - множину С. Тоді множина (AÇB)ÇС зобразиться тією частиною універсальної множини, на якій штрихи накладуться. На правій діаграмі заштрихуємо спочатку вертикальними лініями множину BÇС, а множину А - горизонтальними. Тоді множина AÇ(BÇС) зобразиться тією частиною універсальної множини, на якій штрихи накладуться. Порівнюючи ліву та праву діаграми, бачимо, що множини (AÇB)ÇС і AÇ(BÇС) зображаються однієї й тією ж частиною універсальної множини. А це означає, що рівність (AÇB)ÇС=AÇ(BÇС) справедлива. Отже, закон доведено.

Малюнок № 1.9. Доведення асоціативного закону операції перетину(AÇB)ÇС=AÇ(BÇС) .

Операції об’єднання та перетину множин пов’язані між собою дистрибутивними або розподільними законами. Доведемо один із цих законів, а саме АÈ(ВÇС)=(АÈВ)Ç(АÈС), використовуючи міркування. Оскільки дві множини вважаються рівними тоді, коли кожен елемент першої є елементом другої, і навпаки, кожен елемент другої є елементом першої множини, то доведення складатиметься з двох частин. У першій частині доведемо, що кожен елемент лівої частини рівності належить правій, а в другій – що кожен елемент правої частини є елементом лівої. Виберемо у лівій частині рівності довільний елемент хєАÈ(ВÇС). Якщо хÎАÈ(ВÇС), то згідно означення операції об’єднання множин можливі два випадки: а) хєА і хÏВÇС; б) хÏА і хєВÇС, тоді хєВ і хєС; в) хєА і хєВÇС, тоді хєА, хєВ і хєС.

а) якщо хєА і хÏВÇС, то хÏВ або хÏС. Тоді, згідно означення операції об’єднання хє(АÈВ) і хє(АÈС), а згідно означення операції перетину хє(АÈВ)Ç(АÈС), тобто правій частині рівності.

б) якщо хÏА і хєВÇС, то хєВ і хєС, а тому хє(АÈВ) і хє(АÈС). Отже, хє(АÈВ)Ç(АÈС), тобто правій частині рівності.

в) якщо хєА і хєВÇС, то згідно означення операції перетину хєВ і хєС. Тоді, згідно означення операції об’єднання хє(АÈВ) і хє(АÈС), а згідно означення операції перетину хє(АÈВ)Ç(АÈС), тобто правій частині рівності.

Таким чином, вибравши у лівій частині рівності довільний елемент, який їй належить, ми показали, що будь-який елемент лівої частини рівності належить правій частині рівності. Оскільки в лівій частині елемент ми вибирали довільно, то наші міркування можна повторити для будь-якого елемента лівої частини. Отже, кожен елемент лівої частини рівності є елементом правої частини рівності. Це означає, що (АÈ(ВÇС))Ì((АÈВ)Ç(АÈС)). Перша частина теореми доведена.

Проведемо доведення другої частини: покажемо, що кожен елемент правої частини рівності є елементом лівої. Нехай ує(АÈВ)Ç(АÈС). Тоді згідно означення операції перетину множин маємо: ує(АÈВ) і ує(АÈС). Тут можливі два випадки: а) уєА і уÏВ; б) уÏА і уєВ, а тоді уєС.

а) якщо уєА і уÏВ, то згідно означення операції об’єднання ує(АÈ(ВÇС)), тобто лівій частині.

б) якщо уєВ і уєС, то згідно означення операції перетину ує(ВÇС), а згідно означення операції об’єднання ує(АÈ(ВÇС)), тобто лівій частині. Таким чином, в обох випадках, якщо елемент належить правій частині, то він належить і лівій.

Оскільки елемент у правій частині ми вибрали довільно, то наші міркування можна повторити для кожного із елементів правої частини. Отже, кожен елемент правої частини є елементом лівої. Це означає, що справедливе твердження ((АÈВ)Ç(АÈС))Ì(АÈ(ВÇС)). Другу частину доведено.

Таким чином, у першій частині ми довели, що (АÈ(ВÇС))Ì((АÈВ)Ç(АÈС)), тобто, що кожен елемент лівої частини є елементом правої, а в другій частині – ((АÈВ)Ç(АÈС))Ì(АÈ(ВÇС)), тобто, що кожен елемент правої частини є елементом лівої. Отже, згідно означення рівності множин, маємо АÈ(ВÇС)=(АÈВ)Ç(АÈС), тобто ліва і права частини рівності складаються з одних і тих самих елементів. А це означає, що справедливість закону доведено.

Готуючись до екзамену студент має право доводити відповідні закони будь-яким із наведених способів. Для оволодіння способами доведення пропонуємо студентам довести самостійно всі не доведені закони будь-яким із запропонованих двох способів.

Поиск по сайту: